
- •Глава IV. Бинарные отношения
- •§1. Понятие бинарного отношения и способы его задания
- •Особенно большую роль в математике играют отношения между двумя элементами, которые называют бинарными.
- •§2. Функции и отображения
- •1. Понятия функции и отображения.
- •Можно дать и такое
- •Свойство (5) по закону контрапозиции равносильно следующему свойству:
- •§3. Бинарные алгебраические операции и их свойства
- •1. Понятие бинарной алгебраической операции.
- •§4. Свойства бинарных отношений
- •§5. Отношение эквивалентности
- •§6. Отношение порядка и упорядоченные множества
- •Сводка основных типов отношений
- •Вопросы для самоконтроля
Глава IV. Бинарные отношения
Математика по существу изучает различные типы отношения между элементами различных множеств. Особую роль при этом играют отношения между элементами двух или трех множеств. В первом случае говорят о бинарных отношениях, во втором – о тернарных отношениях. Основной задачей этой главы является определение бинарного отношения, указание способов его задания и его свойств, выделение таких важных типов бинарных отношений как функции и отображения, отношения эквивалентности и порядка. Отдельный раздел посвящается бинарным алгебраическим операциям (т.е. специальному виду тернарных отношений), играющим важную роль в алгебре.
§1. Понятие бинарного отношения и способы его задания
Для обозначения связи между элементами одного или нескольких множеств в математике и в обыденной речи употребляю термин «отношение». Рассмотрим некоторые примеры.
«Число a меньше числа b» (отношение между двумя числами).
«Прямая a параллельна прямой b» (отношение между двумя прямыми на плоскости).
«Студент
 старше
студента
старше
студента
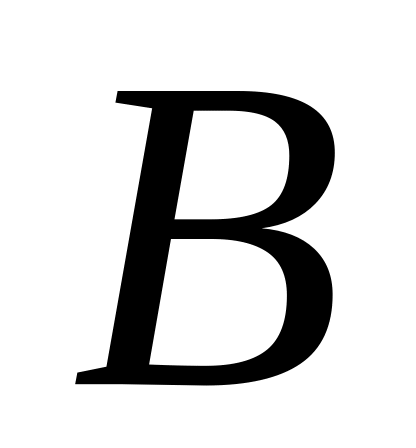 »
(отношение между двумя студентами).
»
(отношение между двумя студентами).«Прямая
 перпендикулярна плоскости
перпендикулярна плоскости
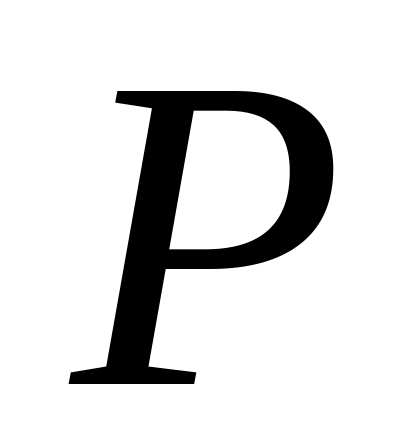 »
(отношение между двумя элементами
различной природы: точками и плоскостями
обычного геометрического пространства).
»
(отношение между двумя элементами
различной природы: точками и плоскостями
обычного геометрического пространства).«Точка лежит между точками и
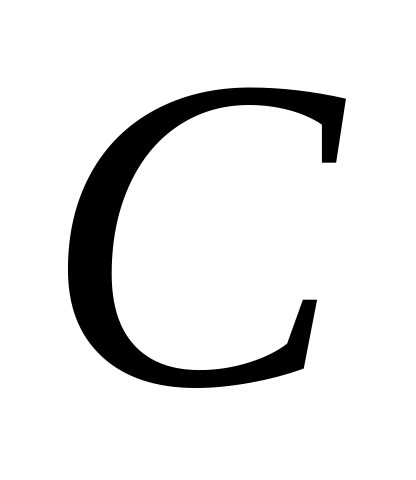 »
(отношение между тремя точками прямой).
»
(отношение между тремя точками прямой).
Особенно большую роль в математике играют отношения между двумя элементами, которые называют бинарными.
Из
примеров ясно, что два элемента
![]() и
и
![]() ,
где
,
где
![]() ,
,
![]() ,
находятся в данном отношении, если и
только если упорядоченная пара
,
находятся в данном отношении, если и
только если упорядоченная пара
![]() обладает некоторым свойством (например,
обладает некоторым свойством (например,
![]() ,
,
![]() и т.д.). Значит, если задано подмножество
и т.д.). Значит, если задано подмножество
![]() ,
то оказывается определенным и некоторое
бинарное отношение между элементами
множеств
и
,
которое будем обозначать тоже через
,
то оказывается определенным и некоторое
бинарное отношение между элементами
множеств
и
,
которое будем обозначать тоже через
![]() .
Очевидно и наоборот – если задано
бинарное отношение
между элементами множеств
и
,
то тем самым определяется подмножество
тех упорядоченных пар
.
Очевидно и наоборот – если задано
бинарное отношение
между элементами множеств
и
,
то тем самым определяется подмножество
тех упорядоченных пар
![]() ,
элементы которых находятся в данном
отношении
.
Эти рассуждения позволяют дать строгое
определение понятия бинарного отношения.
,
элементы которых находятся в данном
отношении
.
Эти рассуждения позволяют дать строгое
определение понятия бинарного отношения.
Определение
1. Всякое
подмножество
декартова
произведения
![]() называется бинарным
отношением между элементами множеств
и
.
При этом, если пара
называется бинарным
отношением между элементами множеств
и
.
При этом, если пара
![]() ,
то говорят, что х
находится с у в отношении
и пишут
,
то говорят, что х
находится с у в отношении
и пишут
![]() .
Если же
.
Если же
![]() ,
то говорят, что х
не находится с у в отношении
и пишут
,
то говорят, что х
не находится с у в отношении
и пишут
![]() .
В частности, если
.
В частности, если
![]() ,
то говорят, что бинарное
отношение
задано на множестве
.
,
то говорят, что бинарное
отношение
задано на множестве
.
Заметим,
что если
– бинарное отношение, то и дополнение
![]() является бинарным отношением. Поэтому
запись
можно прочитать еще и по-другому: «х
находится с
в отношении
является бинарным отношением. Поэтому
запись
можно прочитать еще и по-другому: «х
находится с
в отношении
![]() ».
».
Само
множество
тоже является бинарным отношением. Оно
называется универсальным;
будем обозначать его через
![]() .
Очевидно, что
.
Очевидно, что
![]() для любого
и любого
.
для любого
и любого
.
Как и любые множества, бинарные отношения можно задавать либо перечислением элементов, либо указанием характеристического свойства. Для наглядности используются различные способы представления бинарных отношений, в том числе графическое изображение. Мы укажем три способа.
1. С помощью графов.
Элементы множеств
и
изображаются точками, а тот факт, что
,
изображается стрелкой, идущей от
к
.
Если, в частности,
![]() ,
то всякий раз, когда
,
то всякий раз, когда
![]() ,
вокруг точки, изображающей х, рисуется
петля.
,
вокруг точки, изображающей х, рисуется
петля.
Пример
1. Пусть
![]() ,
,
![]() и бинарное отношение
задано следующим образом:
и бинарное отношение
задано следующим образом:
![]() .
Тогда
изображается следующим графом:
.
Тогда
изображается следующим графом:
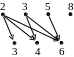
Рис. 1.
Пример
2. Пусть
![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() ,
,
![]() и бинарное отношение
и бинарное отношение
![]() задано следующим образом:
задано следующим образом:
![]() .
Тогда
.
Тогда
![]() изображается следующим графом:
изображается следующим графом:

Рис. 2.
2. Табличный (матричный) способ.
Суть
этого способа в том, что рисуется
таблица, в которой число столбцов на 1
больше, чем элементов в множестве
,
а число строк на 1 больше, чем элементов
в множестве
.
В нижней строке выписывают элементы
множестве
,
а в левом столбце – элементы множества
В. Тогда для каждой упорядоченная
пары
![]() в соответствующий квадратик вписывается
число 1, если
,
и число 0, если
.
Получится таблица (матрица), состоящая
из единиц и нулей, которая полностью
характеризует наше отношение в том
смысле, что если мы выберем упорядоченные
пары
элементов из
в соответствующий квадратик вписывается
число 1, если
,
и число 0, если
.
Получится таблица (матрица), состоящая
из единиц и нулей, которая полностью
характеризует наше отношение в том
смысле, что если мы выберем упорядоченные
пары
элементов из
![]() ,
соответствующие всем единицам таблицы,
то получим в точности наше отношение
.
Для примера 1 соответствующая таблица
имеет следующий вид:
,
соответствующие всем единицам таблицы,
то получим в точности наше отношение
.
Для примера 1 соответствующая таблица
имеет следующий вид:
Таблица 1.
6 |
1 |
1 |
1 |
0 |
4 |
1 |
1 |
0 |
0 |
3 |
1 |
0 |
0 |
0 |
|
2 |
3 |
5 |
8 |
3. Координатный способ.
Строятся две перпендикулярные прямые. На горизонтальной прямой изображаются (точками) элементы множества , на вертикальной – элементы множества . Тогда каждая упорядоченная пара изображается точкой пересечения перпендикуляров, проведенных из точек и . Если , то изображающая эту пару точка выделяется.
Этот метод широко используется в
математической практике, как в школе,
так и в вузе, в том числе и для бесконечных
множеств. В самом деле, если
![]() ,
то уравнение всякой кривой на плоскости
определяет бинарное отношение на
множестве R, а график
этой кривой есть графическое изображение
этого отношения.
,
то уравнение всякой кривой на плоскости
определяет бинарное отношение на
множестве R, а график
этой кривой есть графическое изображение
этого отношения.
Изобразим отношения предыдущих примеров 1 и 2 координатным способом:
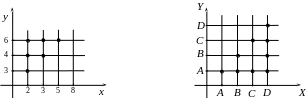
Рис. 3.
Пример
3. Пусть
и
– бинарные отношения на R,
заданные следующим образом:
![]() и
и
![]() .
Тогда координатный метод дает следующие
графические изображения этих отношений:
.
Тогда координатный метод дает следующие
графические изображения этих отношений:
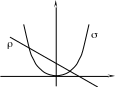
Рис. 4.
Определение 2. Областью определения бинарного отношения называется множество
![]() .
.
Определение 3. Множеством значений (областью прибытия) бинарного отношения называется множество
![]() .
.
Ясно,
что
![]() и
и
![]() .
Графически область определения бинарного
отношения совпадает с множеством
элементов множества
,
из которых выходят стрелки, а множество
значений – с множеством элементов
множества
,
к которым приходят стрелки. Так в примере
1
.
Графически область определения бинарного
отношения совпадает с множеством
элементов множества
,
из которых выходят стрелки, а множество
значений – с множеством элементов
множества
,
к которым приходят стрелки. Так в примере
1
![]() ,
,
![]() ,
а в примере 3
,
а в примере 3
![]() ,
,
![]() ,
,
![]() .
.
По
аналогии с бинарными отношениями
определяются тернарные
отношения, как подмножества декартова
произведения
![]() ;
и вообще, n-арные
отношения определяются как подмножества
декартова произведения
;
и вообще, n-арные
отношения определяются как подмножества
декартова произведения
![]() .
.
В
заключение укажем на связь между
предикатами и отношениями. Пусть
![]() – двухместный предикат, А – ОДЗ
переменной х, В – ОДЗ переменной
у. Этот предикат определяет бинарное
отношение
– двухместный предикат, А – ОДЗ
переменной х, В – ОДЗ переменной
у. Этот предикат определяет бинарное
отношение
![]()
![]() ,
содержащее те и только те пары
,
для которых
,
содержащее те и только те пары
,
для которых
![]() является истинным высказыванием.
Аналогично, трехместный предикат
определяет тернарное отношение, и
вообще, n-местный
предикат определяет n‑арное
отношение.
является истинным высказыванием.
Аналогично, трехместный предикат
определяет тернарное отношение, и
вообще, n-местный
предикат определяет n‑арное
отношение.
