3. Встановлення необхідного обсягу вибірки

При плануванні соціологічного дослідження перед дослідником постає перше завдання – визначення обсягу вибірки, необхідного для забезпечення потрібного рівня точності результату, тобто допустимою похибкою і потрібним рівнем довіри(довірчою ймовірністю).

Для визначення частки деякої ознаки в генеральній сукупності обсяг вибірки визначають за формулою (Кокрен. Методы выборочного исследования.-М.1976.С.89):

, (2.3.1)

де

N - обсяг генеральної сукупності,

n - обсяг вибірки,

- параметр (коефіцієнт), що відповідає рівню надійністі ,

- частка ознаки в генеральній сукупності,

- величина допустимої похибки в частках.

Значення параметра знаходять за таблицею (таблиця № додатку) за рівнем довіри .

Наприклад, якщо досліднику потрібно з ймовірністю 0,95 отримати дані про частку ознаки в генеральній сукупності обсягу = з похибкою, що не перевищує 5% (тобто =0,05) і йому відомо, що шукана частка складає 25% (тобто =0,25), то з таблиці № додатку знаходимо = і за формулою(2.3.1) отримаємо, що потрібно опитати ( = ) респондентів.

Зауважимо, застосування цієї формули потребує хоча б приблизної інформації про частку ознаки в генеральній сукупності, тобто про те, що потрібно визначити. Оскільки

,

то максимального значення добуток досягає при . Тоді при обсяг буде максимальним. Тому підставивши в (2.3.1) отримаємо формулу для визначення обсягу за будь-яких значень частки ознаки в генеральній сукупності (причому обсяг вибірки буде визначено з деяким запасом).

При рівні довіри =0,954, тобто при =2 отримаємо

, (2.3.2’)

За цією формулою обсяг вибірки визначається за обсягом генеральної сукупності і величиною допустимою похибки. Наприклад, за припустимої похибки 5% (рівень довіри 0,954)отримаємо залежності обсягу вибірки від обсягу генеральної сукупності представлені в таблиці 1:

Таблиця 1

N	100	200	300	400	500	600	700	800	900	1000	1500
n	80	133	171	200	222	240	255	267	277	286	316

N	2000	2500	3000	4000	5000	10 000	100 000	Нескінченна
n	333	345	353	364	370	385	398	400

4. Наочні статистики: гістограми та кумуляти

Графічне зображення розподілу

Графічне зображення інтервального статистичного ряду називають гістограмою.

Для побудови гістограми на осі абсцис відкладають інтервали , і на кожному з них будують прямокутник площею , тобто з висотою (рис. 21.1).

Якщо на площині точки з координатами з’єднати відрізками прямої, то отримаємо полігон відносних частот.

Рис. 21.1 Рис.21.2

Емпірична функція розподілу

Емпіричною функцією розподілу називають відносні частоти події в заданій вибірці значень випадкової величини , тобто

,

де

- число значень вибірки, менших за ,

- обсяг вибірки.

Якщо дослід описується неперервною випадковою величиною , то за беруть границі інтервалів (табл. 1).

Тоді ; ; ; … .

З’єднуючи точки 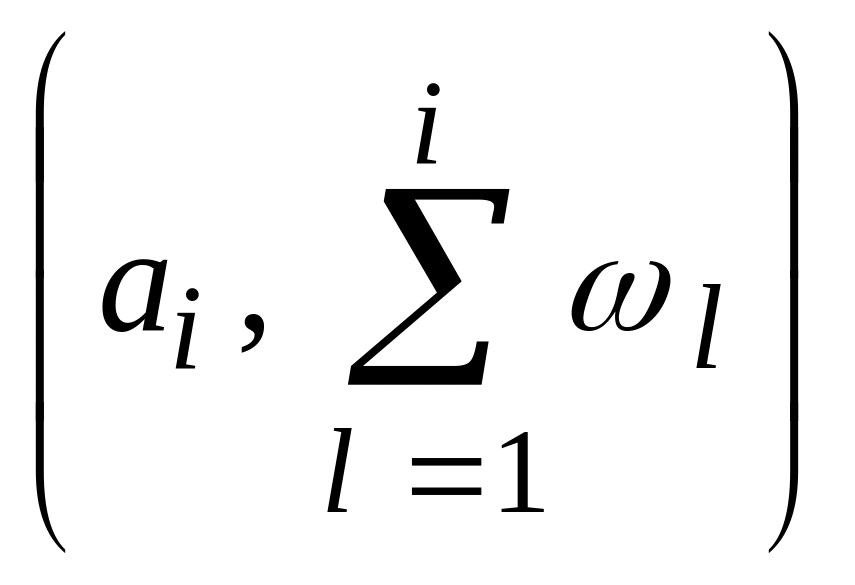, отримуємо графік функції (рис. 21.3).

У випадку коли - дискретна випадкова величина, згідно табл. 3, будуємо східчасту емпіричну функцію розподілу :

Графік функції зображений на рис. 21.4

Рис. 21.3 Рис. 21.4

Приклад 21.1

Маємо вибірку з рівномірного розподілу : ; ; ; ; ; ; ; ; ; ; ; . Скласти інтервальний статистичний ряд, побудувати гістограму та емпіричну функцію розподілу.

 Оскільки досліджується неперервна випадкова величина, і , то діапазон - розбиваємо на інтервалів. Таким чином, маємо інтервальний статистичний ряд

Інтервали

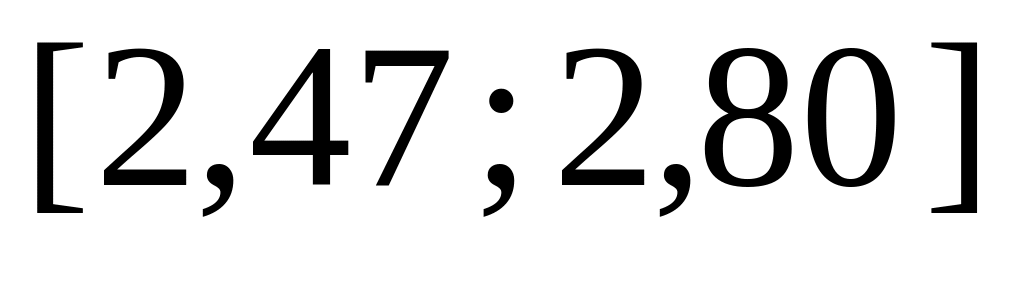
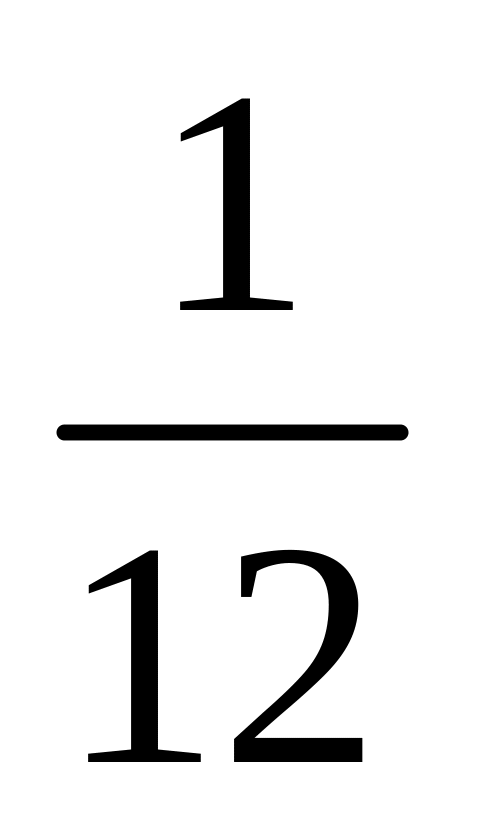
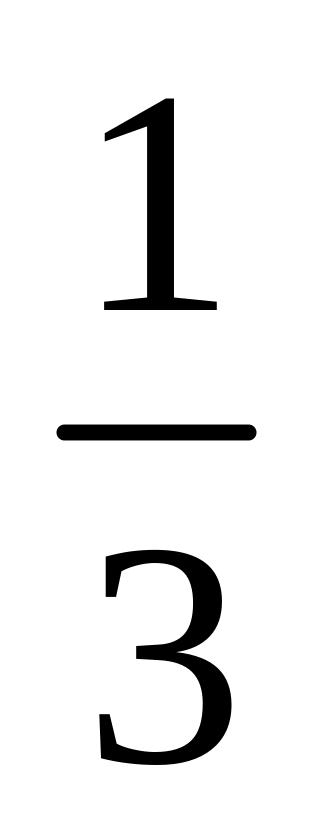
Гістограма частот має вигляд (рис. 21.5).

Емпірична функція розподілу має значення

Графік має вигляд (рис. 21.6) . 

Рис. 21.5 Рис. 21.6

Приклад 21. 2

Задано вибірку дискретної випадкової величини

Побудувати полігон відносних частот та емпіричну функцію розподілу.

 Побудуємо таблицю відносних частот

Полігон відносних частот має вигляд (рис. 21.7)

Емпірична функція розподілу має значення

а її графік зображено на рис. 21.8. 

Рис. 21.7 Рис. 21.8