Лекція 2. Генеральні сукупності та вибірки
Генеральні сукупності та вибірки: означення та параметри.
Репрезентативна вибірка. Процедури формування репрезентативної вибірки.
Встановлення необхідного обсягу вибірки.
Наочні статистики: гістограми та кумуляти.
Описові статистики.
Міри центральної тенденції.
Міри розсіювання (варіації).
Групування
Генеральні сукупності та вибірки: означення та параметри
Генеральна сукупність. Вибірка і способи її задання
Сукупність об’єктів, однорідних відносно деякої кількісної чи якісної ознаки, які підлягають статистичному аналізу називають генеральною сукупністю.
Число об’єктів, які входять в генеральну сукупність називають обсягом (об’ємом) генеральної сукупності.
Об’єкти генеральної сукупності можуть описуватися однією або декількома ознаками, значення яких змінюються при переході від об’єкта до об’єкта.
Нехай
розглядається дослід, який описується
одновимірною випадковою величиною
.
Тоді генеральна
сукупність
це множина
всіх можливих значень випадкової
величини
,
а число елементів в
є об’ємом
(обсягом)
генеральної сукупності.
Розрізняють два види статистичних спостережень: суцільне і вибіркове. На практиці суцільне спостереження проводять не часто. Це зумовлене здебільшого фінансовими обмеженнями і термінами проведення спостереження.Окрім цього, іноді для виявлення досліджуваної ознакидоводиться знищувати(руйнувати) об’єкт. Накінець, якщо генеральна сукупність є дуже великих обсягів, то провести суцільне спостереження фізично неможливо. В такихвипадках проводять вибіркове спостереження, для цього з генеральної сукупності відбирають деяку частину об’єктів. Дані спостережень з вибірки поширюють на ознаку усієї генеральної сукупності.
Сукупність випадково відібраних із генеральної сукупності об’єктів називають вибіркою або вибірковою сукупністю. Число об’єктів вибірки називають обсягом вибірки.
При
незалежних повтореннях досліду випадкова
величина
приймає значення
,
тобто
.
Множина
називають вибіркою,
а число елементів вибірки – об’ємом
(обсягом)
вибірки. При цьому елементи
вибірки називають варіантами.
Випадкові вибірки поділяють на повторні і без повторні. Повторною називають вибірку, при формуванні якої відібраний об’єкт після реєстрації наявності чи відсутності досліджуваної ознаки, знову повертають в генеральну сукупність перед наступним відбором. Якщо відібраний об’єкт після реєстрації не повертається в генеральну сукупність, то вибірку називають безповторною.
На практиці здебільшого користуються без повторним випадковим вибором. Без повторна вибірка, як правило, дає точніші результати. Якщо генеральна сукупність досить великий обсяг, а вибірка складає лише незначну частину цієї сукупності, то відмінності між повторною і безповторною вибірками стираються.
Якщо вибірку розташувати в порядку зростання, то отримаємо варіаційний (варіантний) ряд.
Розподіл вибірки. Графічне зображення розподілу
Нехай
- неперервна випадкова величина і в
результаті
дослідів отримано вибірку у вигляді
варіаційного ряду
.
Діапазон вибірки
ділять на
інтервалів
однакової довжини. Нехай
- кількість варіант вибірки, які попадають
в
-ий
інтервал, тоді
називають абсолютними частотами
спостережуваних даних
– відносними частотами. Зауважимо, що
,
а
.
Таблицю з отриманими інтервалами і відповідними відносними частотами називають інтервальним статистичним рядом (табл. 1).
Таблиця 1.
Інтервали |
|
|
… |
|
|
|
|
… |
|
Якщо
- дискретна випадкова величина з
значеннями
,
тоді таблицю значень
і відповідних абсолютних частот
значень величини
,
називають частотною
таблицею
або розподілом
частот
(табл. 2).
Таблиця 2.
-
Значення
…
Абсолютні частоти
…
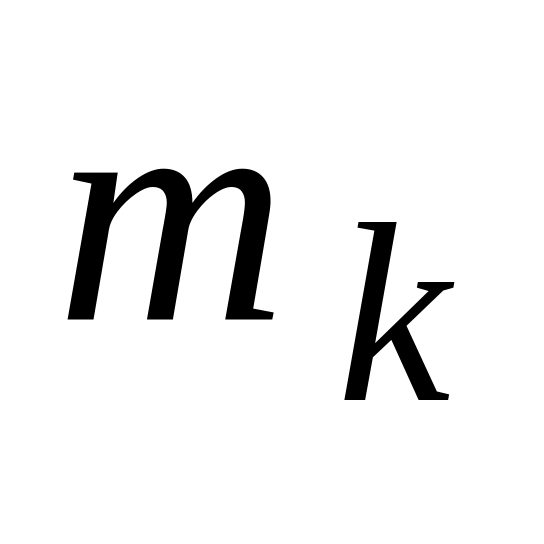
Якщо на
площині нанести точки з координатами
і з’єднати
їх відрізками прямих, то отримаємо
полігон частот, або частотний
багатокутник
(рис.21.2).
Відзначимо,
що
.
Таблицю значень
і відповідних відносних частот
називають розподілом
відносних частот
(табл. 3).
Таблиця 3.
-
Значення
…
Відносні частоти
…
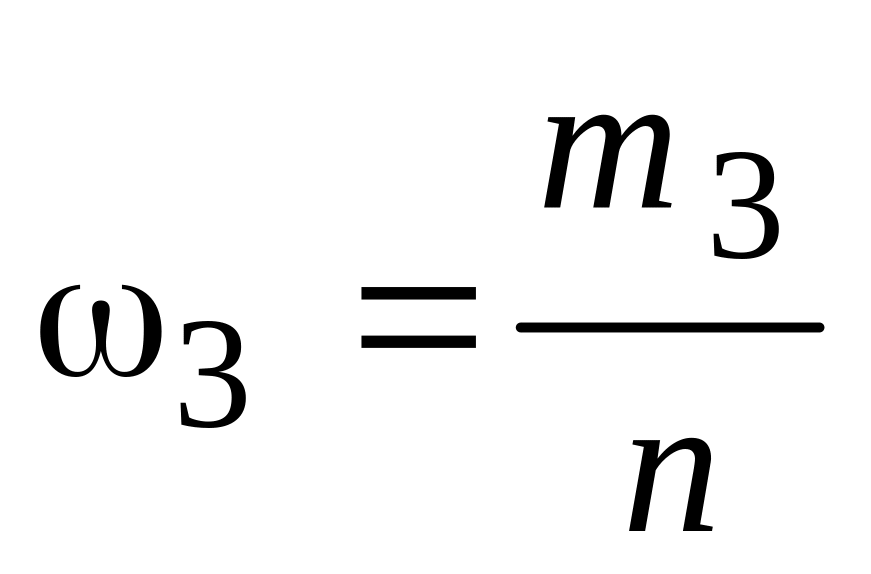