Свойства средней арифметической.
1.Если от каждой варианты отнять какое-либо произвольное число, то новая средняя уменьшится на то же число:
,
откуда
2.Если к каждой варианте прибавить какое-либо произвольное число, то средняя увеличится на это же число:
,
откуда
3.Если каждую варианту разделить на какое-либо произвольное число, то средняя уменьшится во столько же раз:
,
откуда
4.Если каждую варианту умножить на какое-либо произвольное число, то средняя арифметическая увеличится во столько же раз:
,
откуда
5.Если все частоты (веса) разделить или умножить на какое-либо число, то средняя арифметическая от этого не изменится
6.Сумма отклонений вариант, как от простой, так и от взвешенной средней арифметической всегда равняется нулю:
Логически это свойство значит, что в средней арифметической взаимно погашаются отклонения вариант в ту и другую сторону. Все, что касается свойств средней арифметической хорошо изложено у Ряузова Н.Н. “ОТС”.
На математических свойствах средней арифметической базируется понятие моментов распределения.
Моментами распределения в математической статистике называются средние величины тех или иных степеней отклонений вариант от какого-либо числа. Если этим числом является средняя арифметическая, то моменты называются центральными.
Если же отклонения отсчитываются от какого-либо произвольно выбранного числа, то моменты носят название условных.
Если же отклонения отсчитываются от нуля, то моменты носят названия начальных.
В зависимости от степени отклонений моменты распределения называются моментами того или иного порядка. Обычно в математической статистике пользуются моментами первого, второго, третьего и четвертого порядков. Формулы для этих моментов распределения таковы:
Моменты распределения |
Центральные |
Условные |
Начальные |
Первого порядка |
|
|
|
Второго порядка |
|
|
|
Третьего порядка |
|
|
|
Четвёртого порядка |
|
|
|
Центральный момент первого порядка как это вытекает из изложенных выше
свойств средней арифметической (6 свойство), равен нулю.
Условный момент первого порядка играет вспомогательную роль при упрощении вычислений. Начальный момент первого порядка- сама средняя арифметическая.
Моменты 2-го порядка используются в математической статистике для конструирования показателей вариации.
Центральный момент второго порядка представляет собой средний квадрат отклонений и называется дисперсией. После извлечения квадратного корня из величины дисперсии получается среднее квадратическое отклонение, которое является обобщающей характеристикой вариации значений признака. Упростить вычисление среднего квадратического отклонения можно с помощью условного момента второго порядка.
Начальный момент второго порядка не что иное, как средняя квадратическая.
С центральными моментами третьего и четвертого порядков мы встречались при расчете показателей асимметрии и эксцесса.
Материал о моментах распределения доступно изложен у Дружинина “Основные математико-статистические методы в экономических исследованиях”.
2.Средняя гармоническая
- это величина, обратная средней
арифметической. Применяется в тех
случаях, когда в статистической информации
отсутствуют данные о весах, а известны
варианты осредняемого признака «x»
и произведения значений вариантов на
количество единиц, обладающих данным
значением
.
-
средняя гармоническая простая форма
-
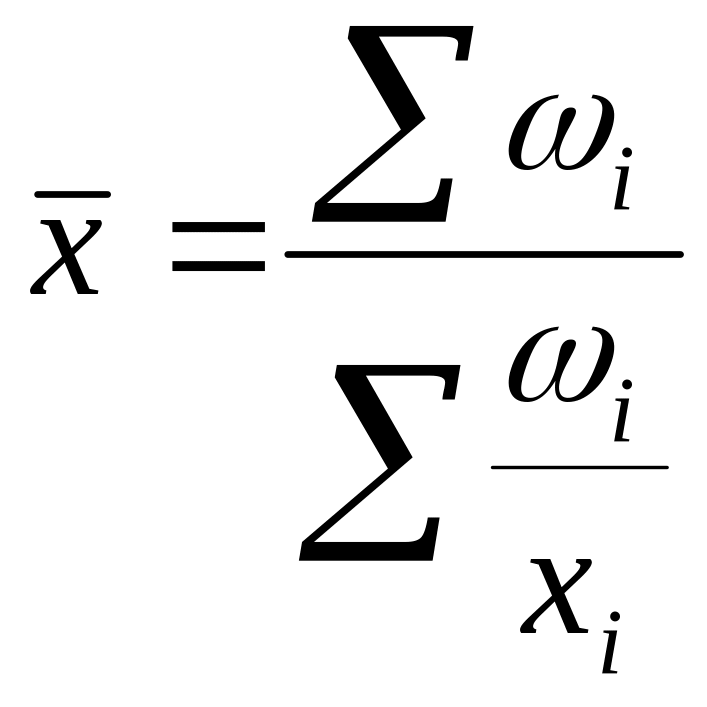взвешенная форма
Вместо гармонической всегда можно рассчитать среднюю арифметическую, но для этого сначала нужно определить веса отдельных значений признака.
-
простая форма
-
взвешенная форма
-
простая форма
-
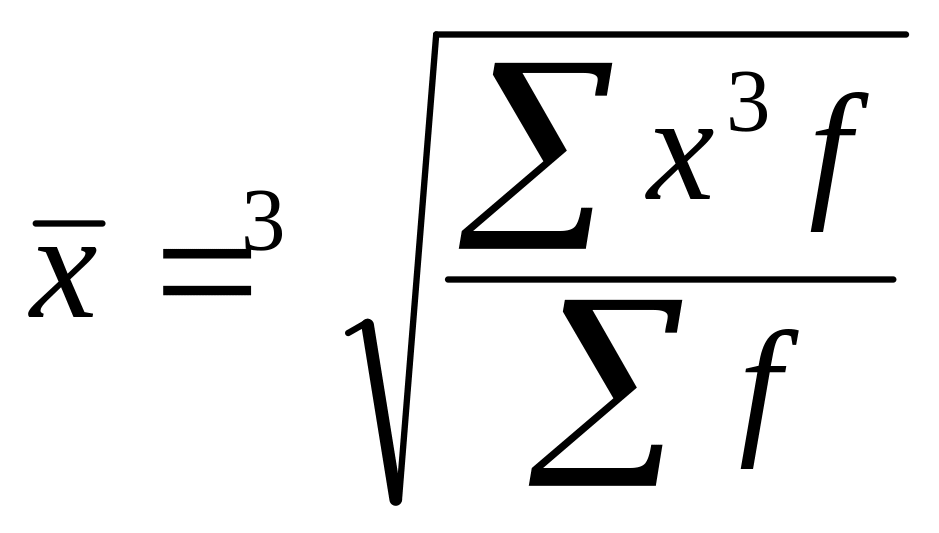взвешенная форма
Данные средние используются в промежуточных расчетах, и самостоятельное значение имеют очень редко.
Средняя квадратическая и кубическая имеют ограниченное применение в практике статистики. Ими пользуются преимущественно для исчисления средних сторон квадратов, средних диаметров труб, стволов и т.п., необходимых для разного рода расчетов, как. Например, для определения запасов древесины на складах и на лесных участках.
4.Средняя геометрическая - вычисляется как корень n- степени из произведения отдельных значений- вариантов признаков.
По содержанию средняя геометрическая отражает среднегодовой темп роста за период, включающий n+1 уровней.
=
-
простая форма
=
-
взвешенная
Широко применяется для расчета среднегодовых темпов роста, причем используются не индивидуальные значения, а их отношение.
5.Средняя хронологическая - используется для расчетов средних уровней в моментных динамических рядах.
Если между моментами времени фиксации проходят равные промежутки времени, то средняя хронологическая имеет вид:
Если между моментами проходят разные промежутки времени, то средняя хронологическая имеет вид:
6.Структурные средние:
а) мода
б)медиана
7.Средняя прогрессивная.
Методика исчисления средней прогрессивной зависит от того, являются ли лучшими наиболее высокие показатели (фондоотдача, продуктивность животных, урожайность с.х. культур) или наиболее низкие (фондоемкость, себестоимость и т.п.)
Сначала исчисляется общая средняя на основе индивидуальных показателей всех единиц совокупности. Затем определяется средняя из индивидуальных показателей, превышающих средний уровень (для первого случая) или не превышающих средний уровень (для второго случая).
Понятие средняя прогрессивная возникло в советской статистике, в связи с указанием Совета Министров СССР, о том, что гос. планы должны быть рассчитаны не на средние арифметические нормы, а на средние прогрессивные нормы, т.е. равняться в сторону передовых.
Пасхавер И.С. “ ОТС” стр.231-233.
Так как средних очень много, возникает вопрос: чем же руководствоваться при выборе формулы в каждом конкретном случае?
При выборе средней определяющим принципом является:
-соответствие этой средней поставленной задаче, цели;
-характер исходных данных.
При этом учитывают правило, что при расчете средних величин, являющиеся числителем и знаменателем показатели должны иметь определенный логический смысл.
Теоретические требования, предъявляемые к расчету средней
1.Средняя величина должна вычисляться и применяться только по качественно однородной совокупности.
2.Правильный выбор единиц совокупности, на которые рассчитывается средняя.
3.Исчисление средних должно производиться на основе массового обобщения фактов или типичной части совокупности.
Суслов И.П. “ ОТС” стр.191-194.