Упражнения:

1. Найти наибольшее и наименьшее значения функции:

2. у= 3х²-6х на отрезке [0;3] ;

2. 2) у=2х³-3х²-36х+10 на отрезке [-5;4].

2. Вычислить промежутки монотонности функций:

1. у= х⁵-5х ; 2) у= х³-3х²-45х+2; 3) у= 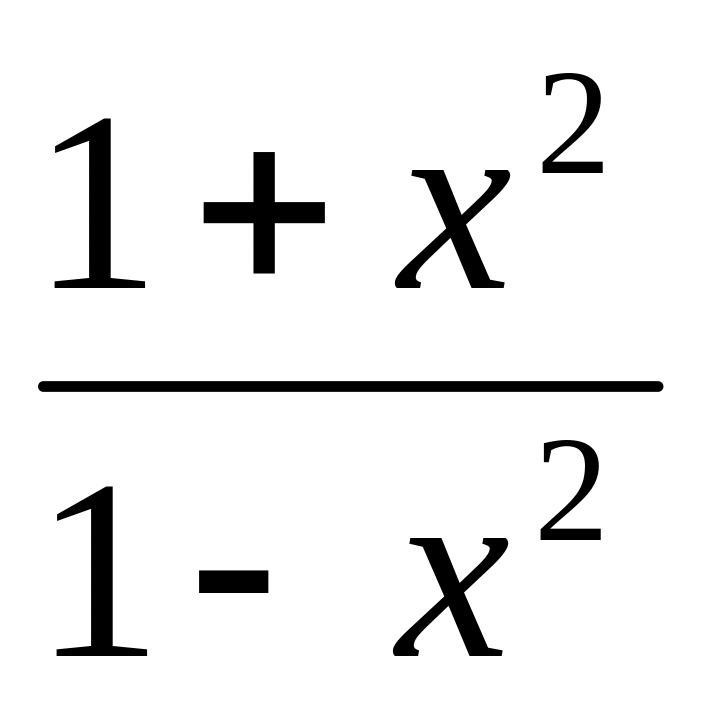; 4) у=х³-2х²-7х+4; 5) у= .

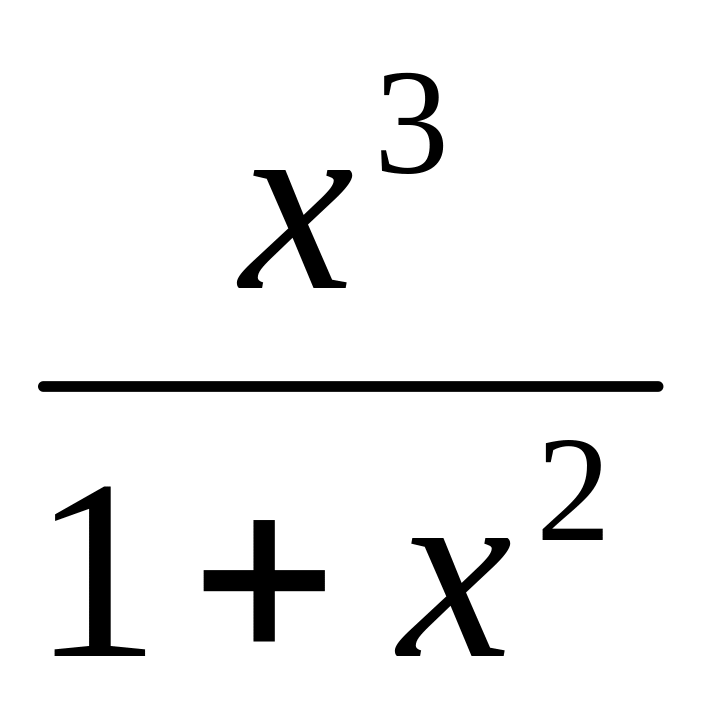2. Вычислить экстремумы функций:

1) ; 2) у=1+2х²- ; 3) у= 3х⁴-4х³; 4) у= ; 5) у= х³-12х²+36х.

2. Вычислить точки перегиба и интервалы выпуклости функций:

1) у=2х³-3х²+15; 2) у=х³-6х²; 3) у= 2х²+lnx; 4) у= х³-3х²+1; 5) у= х⁴-6х²+5.

2. Найти асимптоты графиков функций:

1. у= ; 2) у= ; 3) у= ; 4) у= .

Тема 2.4 Неопределенный интеграл.

Основной задачей дифференциального исчисления является нахождение производной или дифференциала данной функции. Интегральное исчисление решает обратную задачу_ нахождение самой функции по ее производной или дифференциалу.

41. Первообразная функция и неопределенный интеграл .

Определение. Функция F(x) называется первообразной функцией для функции f(x) на промежутке Х, если в каждой точке х этого промежутка F^/(x)=f(x).

Например, является первообразной для функции f(x)=x², так как .

y

y =f(x)+c α

По геометрическому смыслу производной F^/(x) есть угловой коэффициент касательной к кривой

у= F(x) в точке с абсциссой х. геометрически найти

F^/(x)=tg α =f(x)

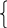y=f(x) α

C

0 x x

Рис. 9

первообразную для f(x)- значит найти такую кривую y=F(x), что угловой коэффициент касательной к ней в произвольной точке х равен значению f(x) заданной функции в этой точке (см. рис.9).

следует отметить, что для заданной функции f(x) ее первообразная определена неоднозначно. Дифференцируя нетрудно убедиться, что функции и вообще , где С –некоторое число, являются первообразными для функции f(x)=x². Аналогично в общем случае, если F(x) – некоторая первообразная для f(x), то, поскольку (F(x)+C)^/=F^/(x) =f(x), функции вида F(x)+C, где С –произвольное число, также являются первообразными для f(x).

Геометрически это означает, если найдена одна кривая у=F(x), удовлетворяющая условию F^/(x)=tg α=f(x), то сдвигая ее вдоль оси ординат, мы вновь получаем кривые, удовлетворяющие указанному условию *( поскольку такой сдвиг не меняет углового коэффициента касательной в точке с абсциссой х) (см.рис.9)

Основное свойство первообразной:

Если F(x) – первообразная для функции f(x) , то выражение вида F(x)+C, где С -произвольное число, задает все возможные первообразные для функции для f(x).

Определение. Совокупность всех первообразных для функции f(x) на промежутке Х называется неопределенным интегралом от функции f(x) и обозначается , где - знак интеграла, f(x)- подынтегральная функция , f(x)dx - подынтегральное выражение . Таким образом,

,

где F(x) – некоторая первообразная для f(x), С- произвольная постоянная.

Операция нахождения неопределенного интеграла от некоторой функции называется интегрированием этой функции.