32. Наибольшее и наименьшее значения функции на отрезке.

Если функция у=f(x) непрерывна на отрезке [a;b], то она принимает на нем наибольшее и наименьшее значения. Наименьшее и наибольшее значение функции может достигаться как в точках экстремума так и в точках на концах отрезка. Так, на рисунке, наибольшее значение функции на конце отрезка х=b, а наименьшее- в точке минимума х₁.

y

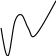
Для отыскания наибольшего и наименьшего значений на отрезке рекомендуется пользоваться следующей схемой:

1⁰. Найти производную f ^/(x).

2⁰. Найти критические точки функции, в которых производная равна нулю или не существует.

3⁰. Найти значения функции в критических точках и на концах

0 a x₁ b x

Рис.3

отрезка и выбрать из них наибольшее f_max и наименьшее f_min.

Пример: Найти наибольшее и наименьшее значения функции

у=(х-2)^2.е^-х на отрезке [0;5].

Решение :

1⁰. f^/(x) = 2(x-2)^.e^-x-(x-2)^2.e^-x= -e^-x.(x-2)(x-2-2)=-e^-x.(x-2)(x-4).

2⁰. f^/(x) =0, -e^-x.(x-2)(x-4)=0

-e^-x=0 или х-2=0 или х-4=0

нет решения х₁=2 х₂=4

3⁰. значения функции в критических точках f(2)=0, f(4)= и на концах отрезка f(0)=4 и f(5)= . Итак, f_max=f(0)=4, f_min(2)=0.

2.34. Исследование функции на выпуклость, вогнутость и точки перегиба.

Нахождение экстремумов во многом определяет структуру графика функции. Определим теперь другие « узловые» точки функции, которые также следует найти, чтобы качественно построить график.

у у у

0 х₁ х₂ х₃ х₄ х₅ х 0 х 0 х

а) б) в)

Рис.4

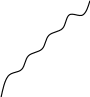
рассмотрим функцию, график которой изображен на рис.4а. эта функция возрастает на всей числовой оси и не имеет экстремумов. Очевидно, однако , ее отличие от функций, изображенных на рис. 4б и 4в. В точках х₁, х_2, х₃, х₄, х₅ график как бы «перегибается». Поэтому такие точки называются точками перегиба, к строгому определению которых мы переходим.

Прежде всего определим различие поведения функции по разные стороны от точек х₁, х_2, х₃, х₄, х_5.

Определение 1. Функция называется вогнутой на промежутке Х, если для любых двух значений х₁, х₂ Х из этого промежутка выполняется неравенство

.

График вогнутой функции расположен над касательной в окрестности точки касания рис. 5а.

Определение 2. Функция называется выпуклой на промежутке Х, если для любых двух значений х₁, х₂ Х из этого промежутка выполняется неравенство

.

График выпуклой функции расположен под касательной в окрестности точки касания рис. 5б.

y y

y=f(x)

y=f(x)

α α

0 x 0 x

а б

Рис. 5

Теорема. Если вторая производная дважды дифференцируемой функции положительна ( отрицательна ) внутри некоторого промежутка Х , то функция вогнута (выпукла ) на этом промежутке.

Таким образом, получаем, если f^//(x)>0 , то функция вогнута, а если f^//(x)<0, то функция выпукла.

Определение. Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в которых функция выпукла и вогнута.

Теорема. Если вторая производная f ^//(x) дважды дифференцируемой функции при переходе через некоторую точку х₀ меняет свой знак, то х₀ есть точка перегиба ее графика.

В окрестности точки х₁ функция выпукла и график ее лежит ниже касательной проведенной в этой точке. В окрестности точки х₂, на которой функция вогнута, картина обратная- функция расположена выше касательной. В

у

0 х₁ х₀ х₂ х

Рис.6

точке перегиба х₀ касательная разделяет график- он лежит по разные стороны касательной. Следует отметить, что если критическая точка дифференцируемой функции не является точкой экстремума, то она есть точка перегиба.

Схема исследования функции на выпуклость, вогнутость и точки перегиба:

1⁰. Найти вторую производную функции f^//(x).

2⁰. Найти точки в которых f^//(x)=0 или не существует.

3⁰. Исследовать знак второй производной слева и справа от найденных точек и сделать вывод об интервалах выпуклости, вогнутости и наличии точек перегиба.

4⁰. Найти значения функции в точках перегиба.

Пример. Найти интервалы выпуклости, вогнутости и очки перегиба графика функции у= х^.(х-1)³.

Решение :

1⁰. Производная. у^/=1^.(х-1)³+3х^.(х-1)²=(х-1)^2.(х-1+3х)=(х-1)^2.(4х- 1);

у^//= 2(х-1)(4х-1)+ (х-1)^2.4=(х-1)^.(8х-2+4х-4)=(х-1)^.(12х-6).

2⁰. у^//=0, (х-1)^.(12х-6)=0

х-1=0 или 12х-6=0

3⁰. у^//>0 на интервалах , следовательно, на этих интервалах

х=1 х=

у^// + - +

х

у 1

функция вогнута; у^//<0 на интервале ( , следовательно на этом интервале функция выпукла, а точки х=1 и х= есть точки перегиба.

4⁰. значения функции в точках перегиба f( )=- , f(1)=0.