Упражнения :

1 Вычислить производную:

№1

1) f(x)= (x+1)¹⁰⁰; 2) f(x)= cos(6x+п); 3) f(x)= tg( ;

4) f(x)= sin6x(x-5) ; 5) f(x)= ; 6) f(x)= .

№2

1. f(x)= arcos( 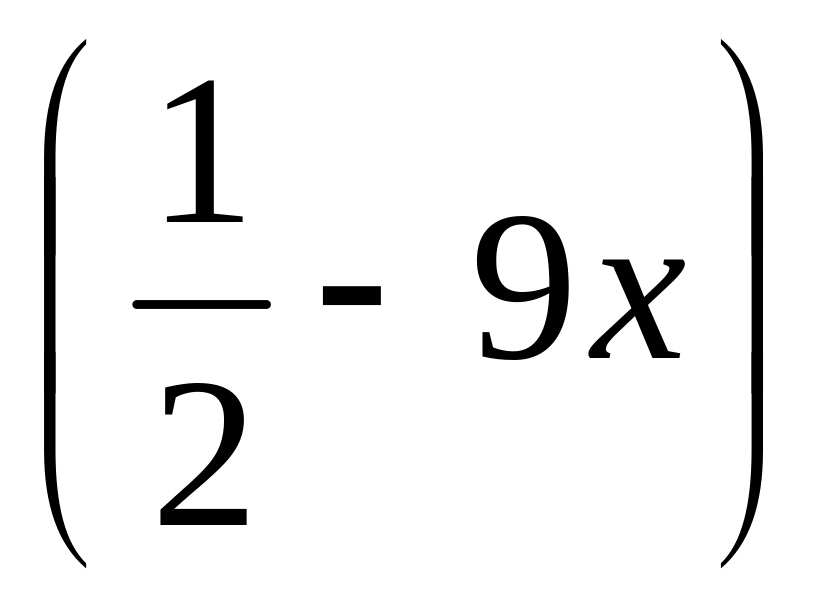; 2) f(x)= ln(1+sin3x); 3) f(x)= ;

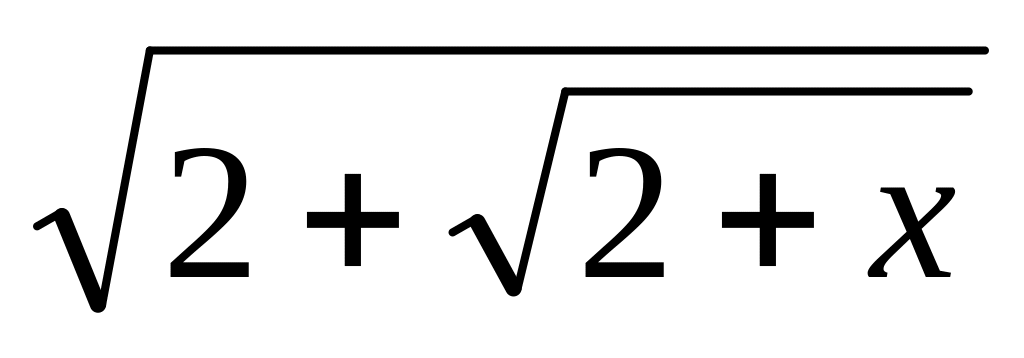4) f(x)= 4^3x(1+tgx); 5) f(x)= ; 6) f(x)= sin²(cos³x).

№3

1. f(x)= x³+2^x-cos3x; 2) f(x)= (x+3)⁴; 3) f(x)= cosx³;

4. f(x)= tg6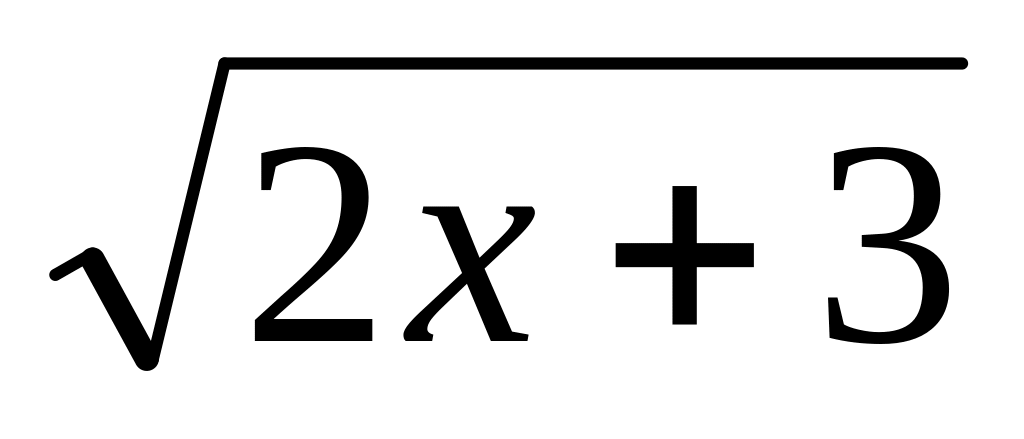x ; 5) f(x)= 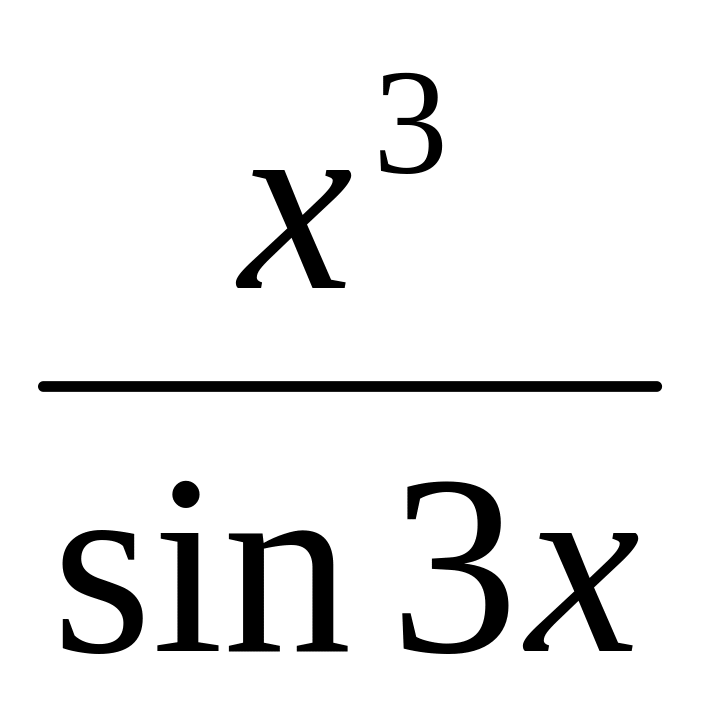; 6) f(x)= ln(6x+5)

№4

1. f(x)= 4x+5cos -arcsin( + ); 2) f(x)= log₃(2-5x);

3) f(x)= 4^x+5arctg( );4) f(x)= ;

5) f(x)= ; 6) f(x)=

№5

1) f(x)= ; 2) f(x)= ln²(x+2); 3) f(x)= arcctg( ^;

4) f(x)= cos²x(5x-3)³; 5) f(x)= ; 6) f(x)= .

2 Написать уравнение касательной:

1. у= -2х²+4х-4, в точке х=3 ; 2) у= в точке х=2;

3 Дана кривая у=х²-2х. Составить уравнение касательных в точках пересечения ее с прямой 3х+у-2=0.

Тема 2.3 Исследование функции методами дифференциального исчисления

2.31 Исследование функций на возрастание и убывание

Теорема (достаточное условие возрастания функции) Если производная дифференцируемой функции положительна внутри некоторого промежутка Х, то она возрастает на этом промежутке.

Теорема (достаточное условие убывания функции) Если производная дифференцируемой функции отрицательна внутри некоторого промежутка Х, то она убывает на этом промежутке.

у у

х

0 х₁ х₂ 0 х₁ х₂

а) Рис.1 b)

Если касательные к кривой в некотором промежутке направлены под острыми углами к оси абсцисс(рис.1.а), то функция возрастает, если под тупыми (рис. 1.b), то убывает.

Пример . Найти промежутки монотонности функции

у= x²-4x+3.

Решение :

у^/=2х-4.

y^/>0 при 2х-4>0 ; y^/<0 при 2x-4<0;

2x>4 ; 2x<4;

x>2 . x<2.

Получаем, что функция возрастает на (2;+∞), а убывает на (-∞;2).

32. Исследование функции на экстремум.

Определение 1. Точка х₀ называется точкой максимума функции f(x), если в некоторой окрестности точки х₀выполняется неравенство f(x) ≤ f(x₀).

О

Значения функции в точках х₀ и х₁ называются соответственно максимумом и минимумом функции. Максимум и минимум функции объединяются общим названием

пределение 2. Точка х₀ называется точкой минимума функции f(x), если в некоторой окрестности точки х₀ выполняется неравенство f(x) ≥ f(x₁).

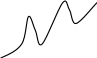у

f(x₀)

f(x₂)

f(x₁)

0 х₀ х₁ х₂ х

Рис.2

названием экстремума функции. Экстремум функции часто называют локальным экстремумом.

В точках локального экстремума дифференцируемой функции ее производная равна нулю.

Поэтому необходимое условие экстремума может быть сформулировано следующим образом.

Для того, чтобы функция у= f(x)имела экстремум в точке х₀, необходимо, чтобы ее производная в этой точке равнялась нулю

( f ^/ (х)=0) или не существовала.

Точки, в которых производная равна нулю или не существует, называются критическими.

Таким образом, если в какой- либо точке имеется экстремум, то эта точка критическая. Очень важно, однако, заметить, что обратное утверждение неверно. Критическая точка вовсе не обязательно является точкой экстремума.

Схема исследования функции у= f(x) на экстремум.

1⁰. Найти производную у^/= f ^/(x).

2⁰. Найти критические точки функции, в которых производная

f ^/(x) =0 или не существует.

3⁰. Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов функции.

4⁰. Найти экстремумы ( экстремальные значения) функции.

Пример . Исследовать на экстремум функцию

у=х(х-1)³.

Решение :

1. Производная. у^/=1^.(х-1)³+3х^.(х-1)²=(х-1)^2.(х-1+3х)=(х-1)^2.(4х-1).

2. Приравнивая производную к нулю, находим критические точки функции: (х-1)^2.(4х-1)=0

(х-1)²=0 или 4х-1=0

х-1=0 4х=1

х₁=0 х₂= .

3. Нанесем критические точки на числовую прямую.

у ^/

+ + х

у 1

Для определения знака производной слева и справа от критической точки х= выберем, например, значения х=0 и х=0,5 и найдем f^/(0)=-1 <0 и f^/(0.5)= >0; следовательно, f^/(x)<0 при всех х< и f^/(х)>0 на интервале ( ;1).

Аналогично устанавливаем, что f^/(x)>0 и на интервале (1;∞).

Согласно условию х= - точка минимума. В точке х=1 экстремума нет.

4. Находим значение функции f_min( )= ( -1)³=- .