5. Правило Лопиталя :

Предел отношения двух функций равен пределу отношения их производных, если последний существует в указанном смысле.

Пример : Вычислить предел:

Решение :

Ответ: 0.

Тема 1.3 Непрерывность функции в точке.

• Функция f(x), определенная на промежутке (а;b), называется непрерывной в точке х_{0 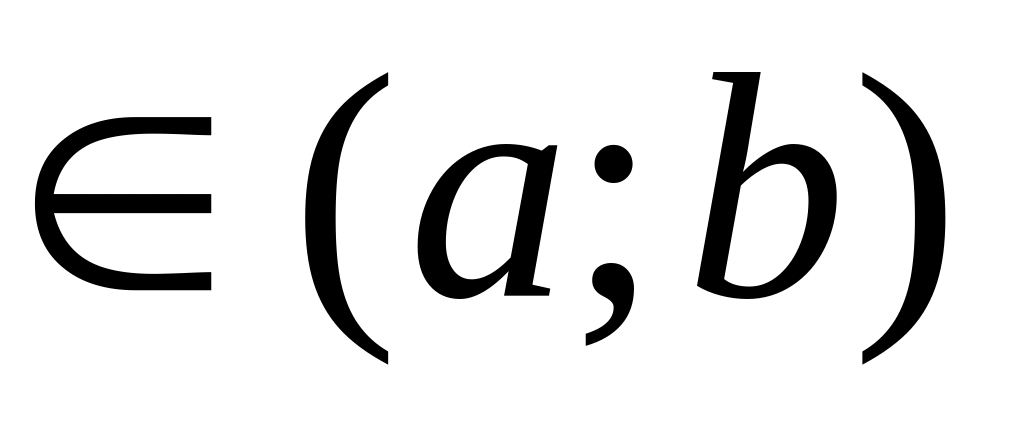,} если:

1. существует предел ;

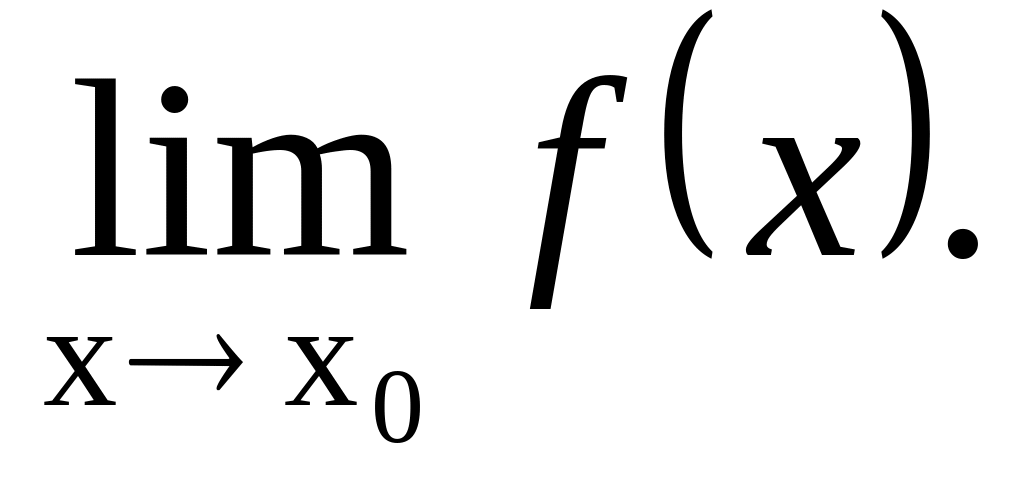2. этот предел равен значению функции в точке х₀, т.е.

Пример : Доказать непрерывность функции

f(x)=3х²+5х, в точке х=2.

Решение:

С другой стороны , значение функции в точке 2 тоже равно 17. Следовательно, равенство выполняется и данная функция непрерывна в точке х=2 .

• если 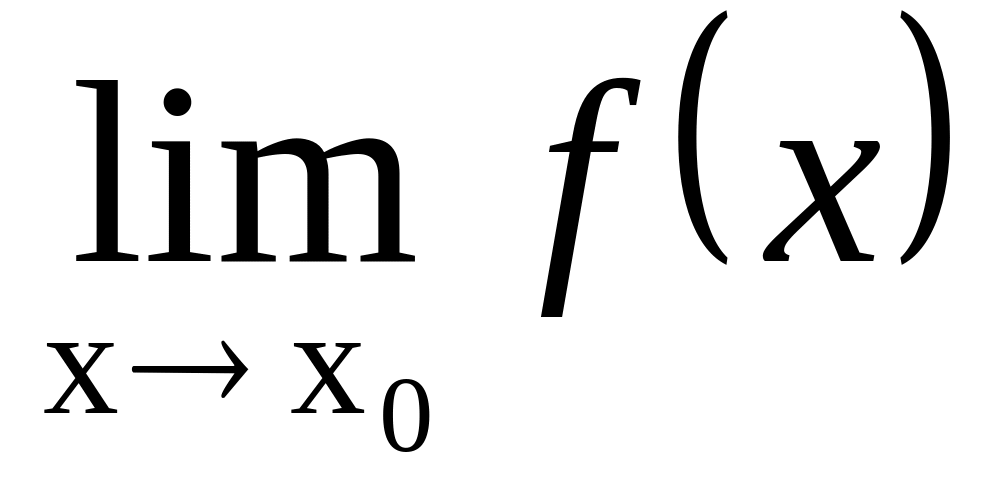существует, но функция не определена в точке х₀, то говорят, что х₀- точка устранимого разрыва. В этом случае можно доопределить функцию f(x) «по непрерывности», положив

.

Пример . Доопределить функцию

в точке х=2 по непрерывности.

Решение :

точка х=2 не принадлежит области определения данной функции, но

Доопределяя функцию f(x) в точке х=2 значением, равным, 4, получаем функцию

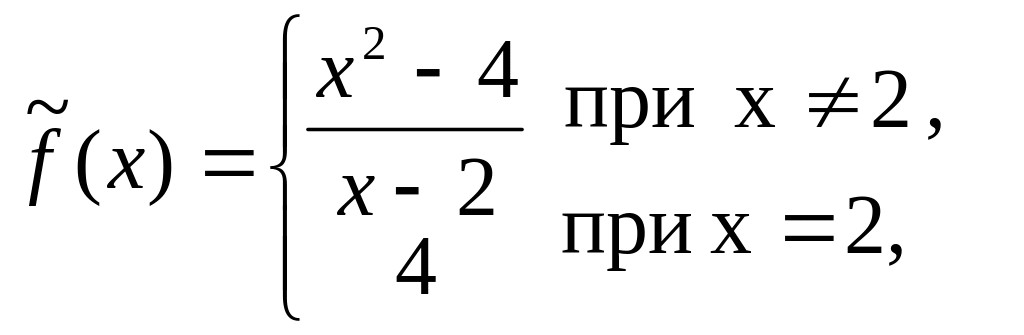
Которая на всей области определения исходной функции совпадает с исходной функцией и будет непрерывной на всей числовой оси.

Ответ : =4.

Упражнения :

Вычислить предел:

№1

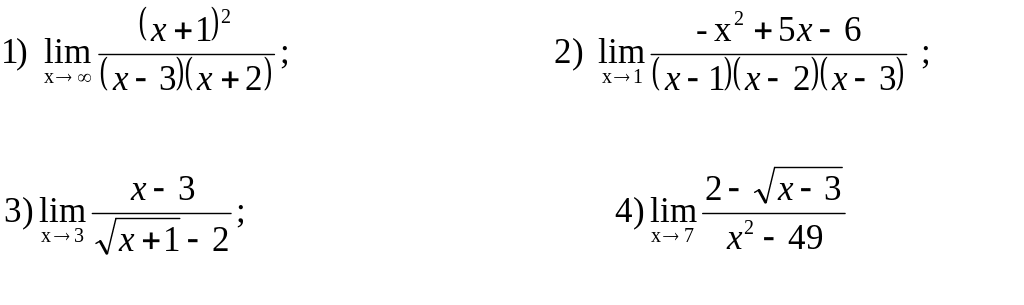
№2

№3

№4

№5

№6

Доопределить функции по непрерывности:

№1 в точке х=3.

№2 в точке х=0.

№3 в точке х=0.

Глава 2. Математический анализ.

Тема 2.1 Определение производной.

Производной функции у=f(x)называется предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю ( если этот предел существует):

Нахождение производной функции называется дифференцированием этой функции.

Геометрический смысл производной: производная есть угловой коэффициент( тангенс угла наклона) касательной, проведенной к кривой в точке х_0, т.е.

y= f(x₀)+f^/(x₀)(x-x₀)- уравнение касательной.

Механический смысл производной: производная пути по времени есть скорость точки в момент

Пример : Написать уравнение касательной функции f(x)= х⁴+5х²-4 в точке х₀=1.

Решение:

1) найдем значение функции в точке х₀: f(1)= ;

2) вычислим производную: f^/(x)=4х³+10х;

3) найдем значение производной в точке х₀: f^/(1)= =14.

Подставляя в формулу уравнения касательной получаем:

у=2+14(х-1)=

Ответ : у= 14х-12.

Тема 2.2 Правила вычисления производной.

1. производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций, т.е.

2. Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, т.е.

3. Производная частного двух дифференцируемых функций может быть найдена по формуле

(при условии, что v ).

Таблица производных

№ п/п	Функция у	Производная у/	№ п/п	Функция у	Функция у/
1	с	0	11	loga u
2	х	1	12	sin u	cos u.u/
3			13	cos u	-sin u.u/
4			14	tg u
5	un	n un-1.u/	15	ctg u
6			16	arcsin u
7			17	arccos u
8	eu	eu.u/	18	arctg u
9	au	aulna.u/	19	arcctg u
10	ln u		20	kx+b	k