Упражнения:

Вычислить частные производные:

1) z=x³y²-2xy³; 2) z= ln(x²+2y³); 3) z= (1+x²)^y; 4) z= ;

5) z= e^3x+5cos9y-ln(x³-y).

Глава 3. Ряды.

Тема 3.1 Числовые ряды. Сходимость рядов.

Определение. Числовым рядом называется бесконечная последовательность чисел и₁, и₂,и₃,…,и_n… соединенных знаком сложения:

и₁+и₂₊,и₃+…+и_n+…=

Числа и₁, и₂,и₃,…,и_n… называются членами ряда, член и_n- общим членом или n-м членом ряда.

Ряд считается заданным, если известен его общий член и_n. Например, ряд с общим членом и_n= имеет вид

Более сложной является обратная задача: по нескольким первым членам ряда написать общий член.

Пример : Найти в простейшей форме общий член ряда:

а) б)

Решение : нетрудно убедиться, что для ряда а) общий член , а для ряда б)

Рассмотрим суммы конечного числа членов ряда:

S₁=u₁, S₂=u₁+u₂, …, S_n=u₁+u₂+u₃+…+u_n.

Сумма n первых членов ряда S_n называется n-й частичной суммой ряда.

Определение :Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм, т.е.

Число S называется суммой ряда. В этом смысле можно записать

Если конечного предела последовательности частичных сумм не существует, то ряд называется расходящимся.

Пример : Найти сумму ряда

Решение : n-я частичная сумма ряда

S_n= .Учитывая, что

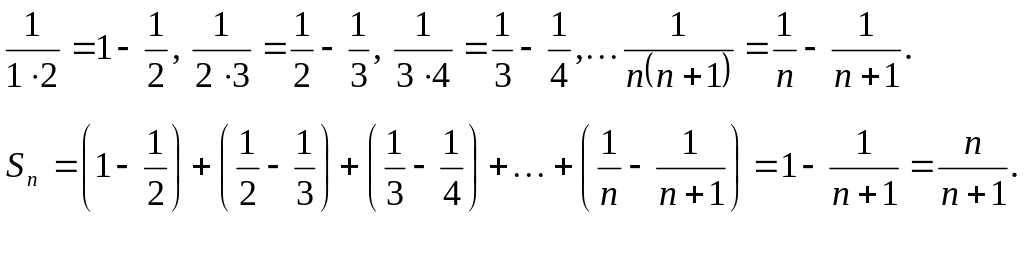
Отсюда, 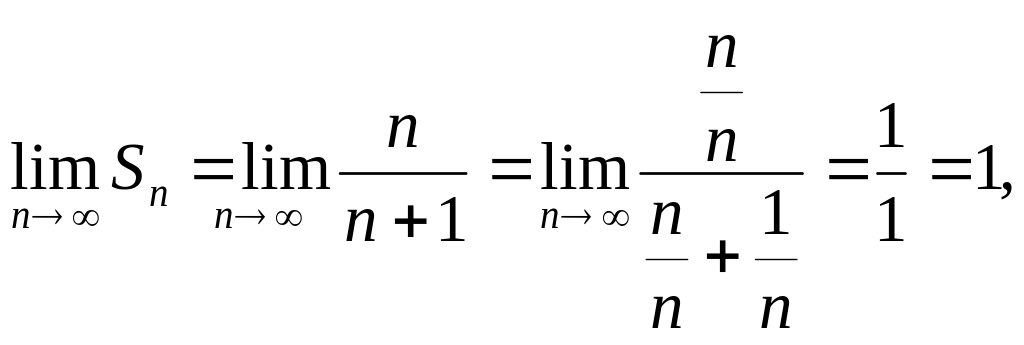т.е. сумма ряда S =1.

Тема 3.2 Необходимый признак сходимости. Гармонический ряд. Геометрический ряд.

Теорема ( необходимый признак сходимости). Если ряд сходиться, то предел его общего члена и_n при равен нулю, т.е.

Пример . Исследовать сходимость ряда

Решение:

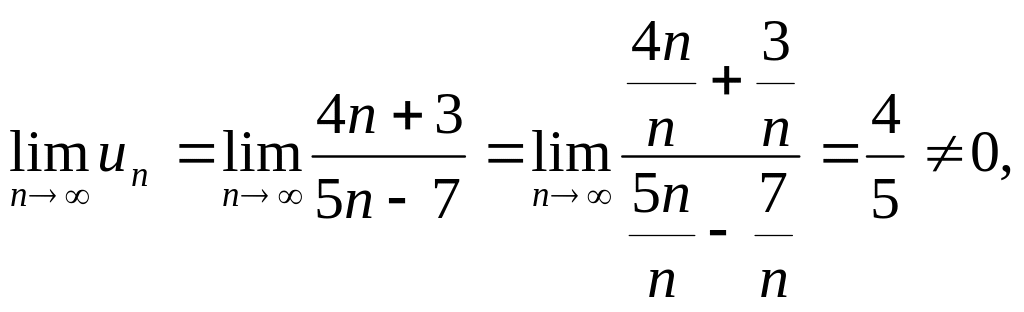т.е. необходимый признак сходимости ряда не выполняется, следовательно, ряд расходиться.

«Эталонные » ряды, часто используемые для сравнения:

1) Геометрический ряд :

a + aq + aq² +_…+aq^n-1+_…= .

Геометрический ряд сходиться к сумме при│q│<1 b и расходиться при │q│≥1.

2) Гармонический ряд.

- расходиться.

3) Обобщенный гармонический ряд.

.

Ряд сходиться при α >1, расходиться при α≤1

Тема 3.3 Ряды с положительными членами .

Теорема (признак сравнения). Пусть даны два ряда с положительными членами: причем члены первого ряда превосходят членов второго ряда, т.е. при любом n

u_{n ≤ .}

Тогда : а) если сходиться ряд (2), то сходиться и ряд(1);

б) если расходится ряд(1), то расходиться и ряд (2).

Пример . Исследовать сходимость ряда

.

Решение:

Сравним данный ряд со сходящимся геометрическим рядом

( его знаменатель q= <1)

Так как члены данного ряда, начиная со второго , меньше членов сходящегося геометрического ряда , то на основании признака сравнения ряд сходиться.

Весьма удобным на практике является признак Даламбера.

Теорема (признак Даламбера). Пусть для ряда с положительными членами существует предел отношения (n+1)-го члена к n-му члену Тогда, если D< 1, то ряд сходиться; если D> 1, то ряд расходиться; если D=1, то вопрос о сходимости ряда остается нерешенным.

Пример . Исследовать сходимость ряда .

Решение:

. Тогда предел отношения будет равен

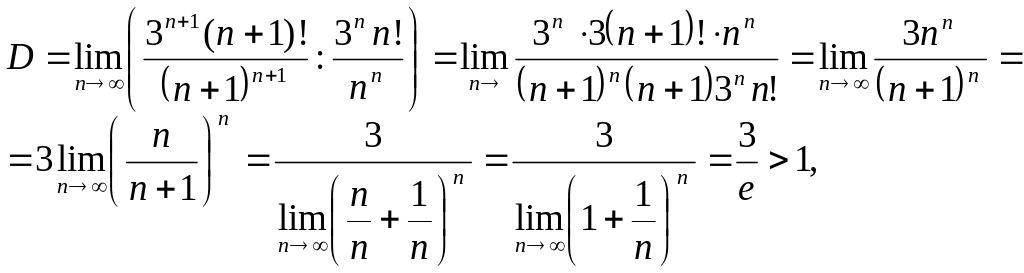
то по признаку Даламбера ряд сходиться.

Замечание 1. Если , то ряд расходиться.

Замечание 2. Если =1, то признак Даламбера ответа о сходимости не дает, и рекомендуется перейти к другим признакам сравнения.