Степенные ряды

Особую роль в теории рядов играют степенные ряды:

, (15.1.3)

где c₀ – постоянные числа, называемые коэффициентами ряда.

В некотором смысле степенные ряды представляют собой обобщение многочленов и по свойствам (будет показано далее) приближаются к многочленам.

Теорема 15.1.1 (теорема Абеля). 1. Если степенной ряд сходится при значении x=x0≠0, то он сходится, причем абсолютно, при любых значениях x, удовлетворяющих условию |x| < |x0|. Если степенной ряд расходится при x=x1, то он расходится при любых значениях x, удовлетворяющих условию |x| > |x1|.

Доказательство

1. Рассмотрим ряд (15.1.4)

Так как этот ряд сходится, то выполняется необходимый признак сходимости, т.е. . Отсюда (в соответствии со свойствами пределов) следует, что последовательность ограниченная, т.е. существует такое положительное число M, что для всех n выполняется

условие . (15.1.5)

Преобразуем ряд (15.1.4) к следующему виду:

Составим ряд из абсолютных величин членов этого ряда. Получим ряд:

(15.1.6)

Сравним этот ряд с рядом , который является геометрическим рядом со знаменателем , который сходится, если , т.е. .

По признаку сравнения (т. 14.1.6) на основании неравенства (15.1.5) следует, что ряд (15.1.6) сходится. Следовательно, сходится, причем абсолютно, ряд (15.1.4) (т. 14.1.13).

2. Пусть ряд расходится при x = x₁. Покажем, что он расходится при любом значении |x| > |x₁|. Предположим противное: ряд сходится при некотором значении x₂, таком, что |x₂| > |x₁|. Но тогда, в соответствии с п.1 ряд должен сходиться и при x₁, что противоречит условию. Таким образом, для всех значений x , удовлетворяющих условию |x| > x₁, ряд расходится.

Геометрически это означает (рис. 15.1):

Е сли степенной ряд сходится в некоторой точке x₀, то он сходится в любой точке, которая ближе к точке x = 0; если степенной ряд расходится в некоторой точке x₁, то расходится в любой точке, более удаленной от точки x=0.

Кроме того, очевидно, что существует некоторое число R ≥ 0, такое, что при |x| < R, степенной ряд сходится, причем абсолютно, а при |x| > R ряд расходится. Это число R называется радиусом сходимости, а интервал (-R,R) – интервалом сходимости степенного ряда.

Найдем радиус сходимости. Рассмотрим ряд, составленный из абсолютных величин степенного ряда (15.1.3). При этом будем полагать, что коэффициенты этого ряда c_n≠0 при любом n. По признаку Даламбера следует: ряд сходится, если .

Найдем

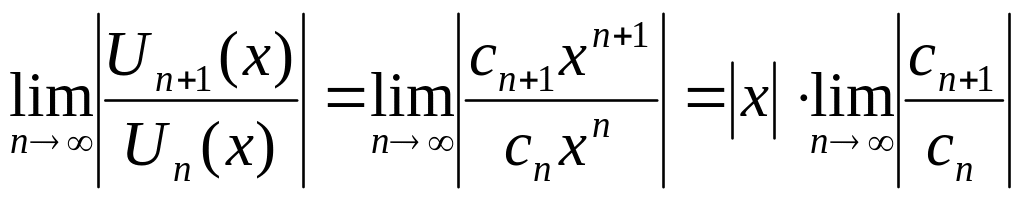
Сходимость ряда, составленного из абсолютных величин членов ряда (15.1.3) обеспечивается условием , откуда .

Если этот предел существует, то он и является радиусом сходимости ряда, составленного из абсолютных величин, т.е.

(15.1.7)

Но в таком случае сходится и сам ряд (15.1.3), причем абсолютно.

Замечание. На концах интервала сходимости, т.е. , очевидно, применение признака Даламбера (или признака Коши) не имеет смысла, так как в этом случае , что оставляет вопрос о сходимости степенного ряда нерешенным. Для решения вопроса о сходимости степенного ряда на концах интервала сходимости следует провести дополнительное исследование числовых рядов, подставив в степенной ряд значения .

Примеры. Найти радиус и интервал сходимости рядов.

1. Выпишем коэффициенты ряда:

.

Исследуем поведение ряда на концах интервала сходимости.

Пусть , тогда получаем ряд .

С равним этот ряд с обобщенным гармоническим рядом , который расходится, так как . Находим .

Существует конечный предел отношения общих членов рядов, значит, оба ряда ведут себя одинаково – расходятся.

Пусть , тогда ряд имеет вид

– это знакочередующийся ряд, удовлетворяющий условиям признака Лейбница. Следовательно, он сходится. Итак, ряд сходится, если .

2. ,

Ряд сходится на всей числовой оси: -∞<x<∞

3. ,

Ряд сходится только при x=0.

Свойства степенных рядов (без доказательств)

1. На любом отрезке [a,b], целиком лежащем внутри интервала сходимости (-R,R), сумма степенного ряда S(x) есть функция непрерывная.

2. Если степенной ряд c₀ + c₁x + c₂x² +…+ c_nxⁿ +…сходится в интервале (-R,R) к сумме S(x), то ряд, полученный почленным интегрированием данного ряда, на отрезке [a,b], целиком принадлежащем интервалу сходимости также сходится, причем абсолютно, и его сумма , иными словами степенной ряд можно почленно интегрировать (как обычные суммы), т.е. если , то .

3. Если степенной ряд сходится в интервале (-R,R) к сумме S(x), то ряд, полученный почленным дифференцированием, также сходится, причем абсолютно, и его сумма , т.е. если , то

Рассмотрим степенной ряд более общего вида

(15.1.8)

Введя новую переменную , получаем рассмотренный ряд (15.1.4). Для него радиус сходимости вычисляется по формуле (15.1.7), т.е. ряд сходится, если , или . Следовательно ряд (15.1.8) сходится, причем абсолютно, внутри интервала .