• Свойства определителей

• 1. При транспонировании матрицы (строки и столбцы меняются местами с сохранением порядка их следования) определитель не меняется.

Пример 7.

• 2. При перестановке любых двух строк (столбцов) определитель меняет только знак.

Пример 8.

• 3. При умножении строки (столбца) на некоторое число определитель умножается на это число.

Пример 9.

• 4. Если все соответствующие элементы квадратных матриц одного порядка одинаковы, за исключением элементов одной i-ой строки, то .

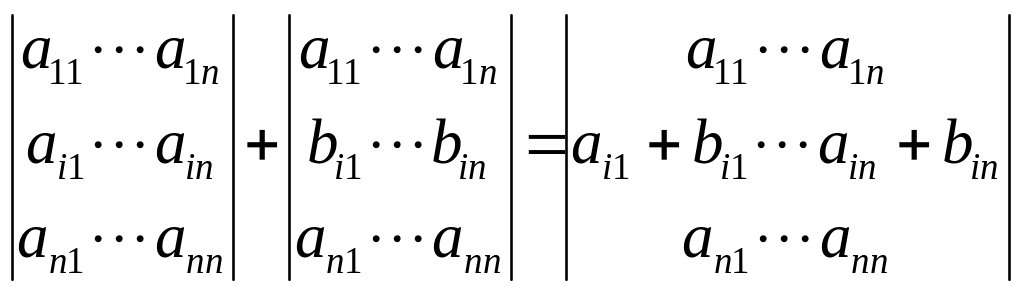• 5. Величина определителя не изменяется, если к элементам некоторой строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженной на некоторое число.

Пример 10.

.

• 6. Определитель равен нулю, если

• - все элементы некоторой строки (столбца) равны нулю.

• - две строки (столбца) одинаковы.

Пример 11. .

• - две строки (столбца) определителя пропорциональны.

Пример 12. .

7. Если каждый элемент кого-либо столбца (строки) определителя есть сумма двух слагаемых, то определитель равен сумме двух определителей: у одного из них элементами соответствующего столбца (строки) первые слагаемые, у другого – вторые.

Пример 13. ,

,

,

-33=-17 + (-16).

Замечание. Есть ещё один способ вычисления определителя: Excel, мастер функций f_x, функция МОПР.

Вопросы для самопроверки

1. Что называется определителем? Каковы основные свойства определителей?

2. Что называется минором и алгебраическим дополнением?

3. Что называется определителем (детерминантом) второго и третьего порядков, каковы их свойства?

4. Каковы способы вычисления определителей?

Литература

1. Краснов М. Л. и др. Вся высшая математика: Учебник. Т. 1– Т. 3. – М.: Эдиториал УРСС, 2000–2001.

2. Натансон И. П. Краткий курс высшей математики. – СПб: Лань, 1997. – 727 c.

3. Щипачев В. С. Основы вышей математики. - М.: Высшая школа, 2009 - 480с.

4. Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах. Ч. IIII. – М.: Высшая школа, 1980.

5. Рябушко А. П. и др. Сборник индивидуальных заданий по высшей математике: Учебное пособие. В 3 ч. – Мн. Выш. Шк., 1991.

6. Веретенников В. Н. Программа дисциплины “Математика” для высших учебных заведений. – СПб.: изд. РГГМУ, 2007.  21 с.

7. Веретенников В. Н. Математика. Учебно-методическое пособие для выполнения контрольных работ. – СПб.: изд. РГГМУ, 2010.  68 с.

8. Веретенников В. Н. Высшая математика. Множества. Элементы линейной алгебры. Векторная алгебра. Учебные пособия. – СПб.: РГГМУ, 2004.

9. Веретенников В. Н. Определители. Матрицы. Системы линейных алгебраических уравнений. Векторная алгебра. Аналитическая геометрия. Индивидуальное домашнее задание. – СПб.: РГГМУ, 2004.

10. А.А.Дадаян Математика. М:Форум-Инфа 2008. Омельченко В.П., Э.В. Курбатова. Математика, – Серия: Среднее профессиональное образование. - Ростов-на-Дону «Феникс»,2008-380с.

11. Омельченко В.П., Э.В. Курбатова. Математика, – Серия: Среднее профессиональное образование. - Ростов-на-Дону «Феникс»,2008-380с.

12. Высшая математика для экономистов: Практикум для студентов вузов, обучающихся по экономическим специальностям/ под.ред Н.Ш.Крамера – М.: ЮНИТА-ДАНА, 2010. Глава 1

13. Высшая математика для экономистов: учебник для студентов вузов, обучающихся по экономическим специальностям/ под.ред Н.Ш.Крамера – М.: ЮНИТА-ДАНА, 2010. Глава 1