
k = 12, m – номер варианта равный номеру студента по журналу
Вариант 1
Задача
1. Написать разложение вектора
 по векторам
по векторам
 .
.
 .
.
Задача
2. Коллинеарны ли векторы
 , построенные по векторам
, построенные по векторам
 .
.
 .
.
Задача
3. Найти косинус угла между векторами
 и
и
 .
.
 .
.
Задача
4. Вычислить площадь параллелограмма,
построенного на векторах
 и
и
 .
.
 .
.
Задача
5. Компланарны ли векторы
,
и
 .
.
 .
.
Задача 6. Вычислить объем тетраэдра
с вершинами в точках
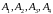 и его высоту, опущенную из вершины
и его высоту, опущенную из вершины
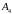 на грань
на грань
 .
.
 .
.
Задача 7. Найти расстояние от точки
 до плоскости, проходящей через три точки
до плоскости, проходящей через три точки
 .
.
 .
.
Задача 8. Написать уравнение плоскости,
проходящей через точку
 перпендикулярно вектору
перпендикулярно вектору
 .
.
 .
.
Задача 9. Найти угол между плоскостями.
 .
.
Задача 10. Найти координаты точки
, равноудаленной от точек
 .
.
 .
.
Задача 11. Найти точку пересечения прямой и плоскости.
 .
.
Задача
12. Найти координаты вектора
 в базисе
в базисе
 , если он задан в базисе
, если он задан в базисе

 .
.
Задача
13. Пусть
 ,
,
 ,
,
 .
Найти:
.
Найти:
 .
.
Задача 14. Найти собственные значения и собственные векторы матрицы.
 .
.
Задача 15. Вычислить пределы.
 .
.
Задача 16. Вычислить пределы.
 .
.
Задача 17. Вычислить пределы.
 .
.
Задача
18. Составить уравнение нормали к данной
кривой в точке с абсциссой
 .
.
 .
.
Задача 19. Провести исследование функций и построить их графики.

Вариант 2
Задача 1. Написать разложение вектора по векторам .
 .
.
Задача 2. Коллинеарны ли векторы , построенные по векторам .
 .
.
Задача 3. Найти косинус угла между векторами и .
 .
.
Задача 4. Вычислить площадь параллелограмма, построенного на векторах и .
 .
.
Задача 5. Компланарны ли векторы , и .
 .
.
Задача 6. Вычислить объем тетраэдра с вершинами в точках и его высоту, опущенную из вершины на грань .
 .
.
Задача 7. Найти расстояние от точки до плоскости, проходящей через три точки .
 .
.
Задача 8. Написать уравнение плоскости, проходящей через точку перпендикулярно вектору .
 .
.
Задача 9. Найти угол между плоскостями.
 .
.
Задача 10. Найти координаты точки , равноудаленной от точек .
 .
.
Задача 11. Найти точку пересечения прямой и плоскости.
 .
.
Задача 12. Найти координаты вектора в базисе , если он задан в базисе
 .
.
Задача 13. Пусть , , . Найти:
 .
.
Задача 14. Найти собственные значения и собственные векторы матрицы.
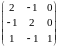 .
.
Задача 15. Вычислить пределы.
 .
.
Задача 16. Вычислить пределы.
 .
.
Задача 17. Вычислить пределы.
 .
.
Задача 18. Составить уравнение нормали к данной кривой в точке с абсциссой .
 .
.
Задача 19. Провести исследование функций и построить их графики.

Вариант 3
Задача 1. Написать разложение вектора по векторам .
 .
.
Задача 2. Коллинеарны ли векторы , построенные по векторам .
 .
.
Задача 3. Найти косинус угла между векторами и .
 .
.
Задача 4. Вычислить площадь параллелограмма, построенного на векторах и .
 .
.
Задача 5. Компланарны ли векторы , и .
 .
.
Задача 6. Вычислить объем тетраэдра с вершинами в точках и его высоту, опущенную из вершины на грань .
 .
.
Задача 7. Найти расстояние от точки до плоскости, проходящей через три точки .
 .
.
Задача 8. Написать уравнение плоскости, проходящей через точку перпендикулярно вектору .
 .
.
Задача 9. Найти угол между плоскостями.
 .
.
Задача 10. Найти координаты точки , равноудаленной от точек .
 .
.
Задача 11. Найти точку пересечения прямой и плоскости.
 .
.
Задача 12. Найти координаты вектора в базисе , если он задан в базисе
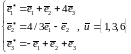 .
.
Задача 13. Пусть , , . Найти:
 .
.
Задача 14. Найти собственные значения и собственные векторы матрицы.
 .
.
Задача 15. Вычислить пределы.
 .
.
Задача 16. Вычислить пределы.
 .
.
Задача 17. Вычислить пределы.
 .
.
Задача 18. Составить уравнение нормали к данной кривой в точке с абсциссой .
 .
.
Задача 19. Провести исследование функций и построить их графики.

