Кинематикалық жұптар және олардың классификациясы

Кинематикалық жұп деп, жоғарыда көрсетілгендей, өз ара салыстырмалы қозғала алатын, жанасқан екі звеноның қосылысын айтады.

Басқа материалдық объектілердің, материалдық нүктенің немесе механикалық системаның қозғалыстарын шектеуді байланыс деп атаймыз.

Кинематикалық жұп өз құрамындағы звенолардың өз ара салыстырмалы қозғалысына белгілі U санды байланыс жасайды, мұның өзі осы жұптар звеноларының өз ара салыстырмалы қозғалысының еркіндік дәрежесін U санына кемітеді.

Осылайша кинематикалық жұп звеноларының еркіндік дәрежесін көрсететін саны мынаған тең болады:

немесе 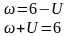(2.3)

Байланыс U саны тек бүтін сан болады және бірден беске дейін өзгереді, яғни

(2.4)

2.1-таблица. Кейбір звенолар мен кинематикалық жұптардың конструкциялық және шартты кескіндері

2.3-сурет. І кластық кинематикалық 2.4-сурет. ІІ кластық кинематикалық

жұп. жұп.

Егер байланыс саны болса, онда звенолар жанаспайды және олар кинематикалық жұп құрамайды, ал егер болса, онда звенолар өз ара салыстырмалы қозғалысын мүлде жоғалтады және кинематикалық жұп құрайтын екі звено қатаң қосылысқа айналады, яғни бір звено құрайды.

Енді еркін шарды алып, оның әр түрлі звенолармен кинематикалық жұптарды құрайтынын қарастырып көрелік. Байланыс санының өсуіне сәйкес кинематикалық жұп класының біртіндеп өзгеретінін көрсетелік:

1. Шарды жазықтыққа орналастырсақ (2.3-сурет), кинематикалық жұп аламыз, бұл кинематикалық жұп әрбір звеноның өз ара салыстырмалы қозғалысында осы бойында жылжуын шектейді және бұл байланыстың теңдеуі мына түрде болады:

. (2.5)

Байланыс саны , сондықтан бұл кинематикалық жұпты 1 класқа жатқызу қажет.

2. Шарды, ішкі диаметрі берілген шардың диаметріне тең, цилиндрге орналастырсақ, кинематикалық жұп (2.4-сурет) аламыз, бұл кинематикалық жұп звенолардың өз ара салыстырмалы қозғалысына екі байланыс жасайды ( ), осы арқылы ол екі координаталар осі бойынша қозғала алмайды. Кинематикалық жұп II класқа жатады және бұл байланыстардың теңдеулері мына түрде болады:

. (2.6)

3. Шарды, ішкі диаметрті осы шардың диаметріне тең, бос шарға орналастырсақ, III класқа жататын кинематиклық жұп (2.5-сурет) аламыз, бұл кинематикалық жұп звенолар қозғалысына үш байланыс жасайды, оны мына теңдеулермен көрсетуге болады:

(2.7)

2.5-сурет. ІІІ кластық 2.6-сурет. ІV кластық 2.7-сурет. V кластық

сфералық жұп. кинематикалық жұп. кинематикалық жұп.

және осы арқылы осьтер бойында болатын мүмкін үш орын ауыстыруды жоққа шығарады.

4. Саусақты шарды, ішкі диаметрі берілген шардың диаметріне тең саңлаулы қуыс шарға орналастырып, саусақтың диаметрін саңлаудың еніне тең етіп алсақ, IV кластық кинематикалық жұп (2.6-сурет) аламыз, бұл кинематикалық жұп звенолардың өз ара салыстырмалы қозғалысына төрт байланыс жасайды, мұнда байланыстар теңдеулері мынадай түрде өрнектеледі:

(2.8)

5. Жоғарыда көрсетілген шар саңлауының ұзындығын саусақ диаметріне дейін қысқартсақ, V кластық кинематикалық жұп (2.7-сурет) аламыз, мұнда кинематикалық жұп звенолардың өз ара салыстырмалы қозғалысына 5 байланыс жасайды, олар мынадай теңдеулермен өрнектеледі:

. (2.9)

Бұл жағдайда кинематикалық жұп звеноларының өз ара салыстырмалы қозғалысы, яғни қалған еркіндік дәрежесінің саны бірге тең 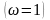және бұл қозғалыстың кинематикалық теңдеуін былай өрнектеуге болады:

,

Мұндағы - саусақ осіне сәйкес болатын осін айналу бұрышы.

Егер кинематикалық жұптағы кез келген звено нүктесінің салыстырмалы қозғалысының траекториялары жазық қисық болса, онда мұндай жұп жазық жұп деп аталады. Егер салыстырмалы қозғалыстың тераекториялары кеңістік қисық болса, онда мұндай кинематикалық жұп кеңістік жұп деп аталады.

2.3 таблицада көрсетілген механизмдердің әр түрлі семьялықтағы структуралық формулаларының әрқайсысын В.В.Добровольскийдің структуралық формуласынан алуға болады:

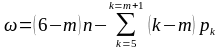, (2.10)

Мұндағы - механизм семьялылығының номері немесе жалпы байланыстар саны ;

- кинематикалық жұптың класы ;

- звенолар саны.