Правило предпочтения
min {ti}
min {zi}
min {i}
Выбранные мероприятия устанавливаются как можно раньше, если для его реализации хватает ресурсов для выполнения без прерывания.
На практике формируется несколько вариантов систем правил, приоритетов, с помощью которого формируются альтернативы. Среди полученных альтернативных вариантов расписаний реализаций мероприятий выделяется наилучший, который позволит получить выполнение всех программ мероприятий за:
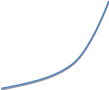
Вmin
= max{gi},
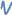Bmax
=
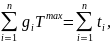Tmin = max{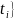
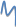
Описание
графика – по вертик Результат
Лучший вариант «1», т.к. эффекивность
проекта
достигается раньше
Социальная значимость может быть оценена с точки зрения прогрессивности динамики реализации мероприятий программы (результат %)
«упущенная
выгода» - при переносе реализации
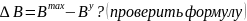
Yb>
3.Имитационные модели на ориентированных графах (орграф)
При построении модели на орграфе показатели ( факторы), исследующие социально – экономические процессы отображаются вершинами графа, а воздействие 1-го показателя на другой отображается дугой
(п)
в орграфе может быть несколько или не быть вовсе начальных вершин, в которых не входит ни одной дуги
в орграфе обязательно должны быть замкнутые контуры (циклы)
(1)
(5)
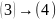
Аналитическое отражение орграфа реализуется через матрицу смежности. ( не вся инфа) j
i |
1 |
2 |
3 |
4 |
5 |
1 |
0 |
1 |
0 |
0 |
0 |
2 |
0 |
0 |
1 |
0 |
0 |
3 |
1 |
0 |
0 |
1 |
0 |
4 |
0 |
0 |
0 |
0 |
1 |
5 |
0 |
0 |
0 |
1 |
0 |
(Ставим единички (выходит по i, направлена в j) Пример - из 1 в 3)
Матрица смежности заполняется 0 и 1 по принципу: если из I идет дуга к j, то в ячейке ставим 1, если нет, то 0. Матрица показывает воздействие одного фактора на другой.
Матрица достижимости — максимизированная (?) матрица смежности. Показывает информацию о путях между вершинами орграфа.
Непосредственное воздействие одного элемента на другой
АЛГОРИТМ
Переносим первую строку
В формированной матрице находим первую попавшуюся 1, не отмеченную *
Пусть первая попавшаяся неотмеченная 1 найдена в j, тогда проводится поэлементное суммирование элементов строки i со строкой j исходной матрицы смежности по правилу булевой алгебры (0+0=0 ; 1+0=1 ; 1+1=1)
Поиск контуров в орграфе.
На главной диагонали определяем первую попавшуюся неотмеченную единицу. Если ее нет, то в орграфе контуры отсутствуют. В противном случае, для найденной первой попавшейся 1 находится поэлементное произведение строки столбца на которой она стоит.
h=(1,1,1,0,0)
В полученном векторе единицы соответствуют номерам вершин графа, входящих в замкнутый контур.
После определения вершин, входящих в замкнутый контур в максимальной матрице смежности, обнуляются соответствующие строки и столбцы.
h=(0,0,0,1,1)
Моделирование с помощью знаковых орграфов.
В знаковых орграфах на дугах указываются знаки «+», если влияние одного показателя на другой прямо-пропорционально. И «-», если воздействие одного показателя на другой обратно-пропорционально.
Импульсные процессы.
S-шаг расчета
Vi(S) –значение i показателя на шаге S
Vj(S)- значение j показателя на шаге S
Pi(S)=Vi(S)-Vi(S-1)
Pi(0)=начальному импульсу
Vj(S+1)=Vl(S)+ ∑eij*Pi(S)
Этапы построения моделей и прогнозируемой динамики на основании орграфа.
Формирование набора показателей для отображения в модели на орграфах
Формирование непосредственного воздействия между выбранными показателями для отображения в виде дуг орграфа
Определение знаков на дугах орграфа
Выяснение начального импульса Ро (Начальный импульс может воздействовать на 1 или несколько показателей одновременно)
Проведение расчетов на основе формул импульсного процесса для заданного количества шагов
Выявление направлений изменения показателей на основе полученных расчетов