Кривые зависимости относительно сопротивления р от кп

а – расчетные кривые, построенные по формулам: Арчи – Хамбла.

б - экспериментальные кривые для песчано-алевролитовых пород.

2.2. Удельное сопротивление нефтеносных и газоносных пород.

Коэффициент увеличения сопротивления.

Б олее тесно с нефтенасыщенностью пласта связано отношение удельного сопротивления пласта к удельному сопротивлению этого же пласта при полном заполнении его пустот ПВ:

Это отношение называют коэффициентом увеличения удельного электрического сопротивления пласта (коэффициентом увеличения сопротивления).

У становлена связь коэффициента увеличения сопротивления с коэффициентом водонасыщенности

где n – показатель степени водонасыщенности, главным образом зависящий от глинистости пород и свойств пластовых флюидов.

Г еофизические методы исследования разрезов скважин Электрический каротаж Классификация электрического каротажа

Измеряемые величины: U_ПС – потенциал самопроизвольной поляризации;

ρ_к – кажущееся удельное сопротивление; δ_к – кажущаяся удельная проводи­мость; ξ_к – кажущаяся диэлектрическая проницаемость.

Результаты решения прямых задач могут быть представлены в виде кривых изменения ρ_к вдоль оси скважины (формы кривых сопротивления), в виде семейств кривых зависимостей ρ_к от ρ_п (палеток) или в виде таблиц значений ρ_к.

Цель решения прямых задач ЭК состоит в том, чтобы обеспечить решение обратной задачи – нахождение истинных электрических свойств и геометрии среды по известным значениям электрического поля в отдельных точках скважины, т.е. по данным измерений каротажным зондом. Решение обратной задачи осуществляется в процессе интерпретации результатов материалов каротажа при помощи методических приемов и интерпретационных палеток, которые будут более подробно рассмотрены в дальнейшем.

Электрический каротаж состоит в основном из двух модификаций: метода сопротивлений и метода самопроизвольного возникающего электрического поля естественный, собственных потенциалов.

Основы теории электрического каротажа по методу сопротивления

3.1 Общие сведения

Для определения удельного сопротивления горных пород в скважине используется источник тока, создающий в окружающей среде электрическое поле.

Допустим, что в неограниченную проводящую среду при помощи электродов А и В (рис. 1) пропускают ток, создающий в ней электрическое поле.

Электрическое поле, созданное в проводящей среде токовыми электродами A и В, тождественно электростатическому полю зарядов электродов А и В, помещенных в непроводящую среду. Разница заключается лишь в том, что в электростатическом поле заряды неподвижны, а в проводящей среде заряды находятся в движении, непрерывно возобновляясь источником тока.

Поэтому рассмотрим вначале электростатическое поле.

Электростатическое поле характеризуется напряженностью в каждой своей точке, численно равной силе, действующей на единицу положительного заряда, помещенного в эту точку, и имеющей направление этой силы, следовательно, напряженность — это вектор (рис. 2, а и б).

Рассмотрим напряженность поля в произвольной точке A, отстоящей от заряда е на расстоянии r.

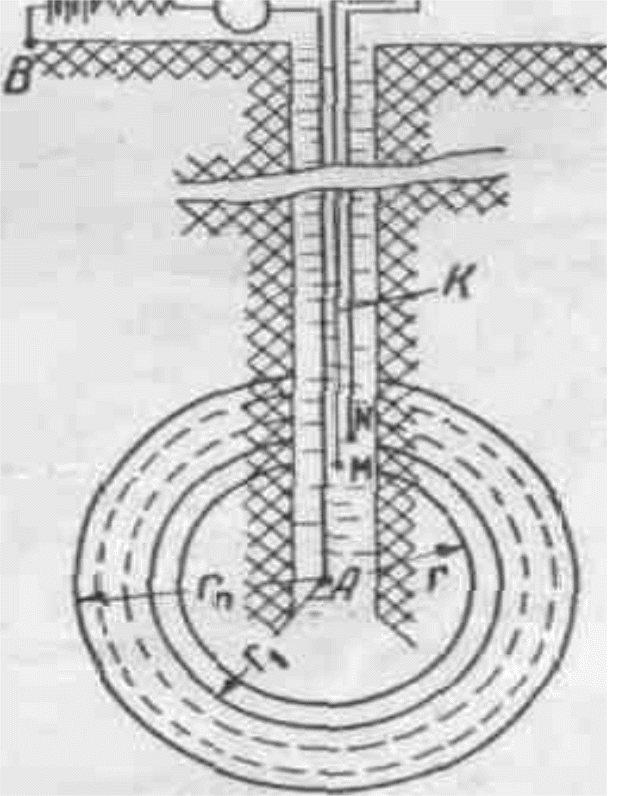
Рис. 1

Схема измерения кажущегося удельного сопротивления

А и В — токовые электроды; М и N — измерительные электроды; II — измерительный прибор; К — трехжильный кабель; Е — источник тока; R — сопротивление для установки силы тока в цепи питания; Aм — амперметр.

По закону Кулона сила F, действующая на положительный заряд e_o, помещенный на расстоянии r от заряда e, равна касательной к ней (рис. 3).

(1)

Отсюда напряженность в точке А будет:

(2)

Введем понятие о линии напряженности электрического поля, называемой чаще силовой линией. Под силовой линией подразумевают такую линию, в каждой точке которой вектор напряженности направлен по касательной к ней.

Силовая линия электрического поля определяет в каждой точке, через которую она проходит, направление напряженности поля Е. Силовые линии соответствуют путям, вдоль которых должен был бы двигаться положительный заряд. При помощи силовых линий можно наглядно изобразить силовое поле; при этом густота силовых линий выбирается пропорционально напряженности.

Примеры изображения электрических полей при помощи силовых линий.

1. Силовые линии точечного заряда. Легко видеть, что силовые линии точечного заряда это прямые линии, выходящие из заряда, если он положительный, и входящие в заряд, если он отрицательный (рис. 4, а и б). Касательные к силовым линиям совпадают в этом случае с самими линиями и направлены в каждой точке в том же направлении, что и напряженность.

Рис. 4 Силовые линии точечного заряда Рис. 5 Силовые линии двух

точечных зарядов

а – положительного; б – отрицательного а – одноименных; б - разноименных

2. Силовые линии двух точечных зарядов. На рис. 5 а представлены линии двух точечных равных и одноименных зарядов; на рис. 5 6 — двух точечных разноименных зарядов, численно равных друг другу, иными словами силовые линии диполя.

Понятие о потенциале. Потенциал данной точки поля численно равен работе, которую нужно совершить для перемещения единичного положительного заряда из этой точки в бесконечно удаленную, потенциал которой равен нулю.

Потенциал есть величина скалярная и в каждой точке поля имеет вполне опреде­ленное значение, поэтому может служить, характеристикой поля наравне с напряженностью Е.

В системе CGSE за единицу разности потенциалов принимается разность потенци­алов между двумя точками, при перемещении между которыми единичного заряда совершается работа в 1 эрг. В практической системе за единицу разности потенциалов принимается величина в 300 раз меньшая, называемая вольтом.

Потенциал электростатического поля представляет собой функцию, которая изменяется от точки к точке и убывает в направлении хода силовой линии. В каждом реальном случае можно выделить совокупность точек, потенциалы которых одинаковы.

Геометрическое место точек постоянного потенциала называют эквипотенциальной поверхностью. Если путь перемещения заряда замкнут по эквипотенциальной поверхности, то работа электрических сил равна нулю.

Из физики известно, что потенциал точечного заряда е в точке, отстоящей от него на расстоянии r, равен

(3)

Следовательно, эквипотенциальная поверхность с постоянным значением r есть сфера с центром в точечном заряде рис. 6, а.

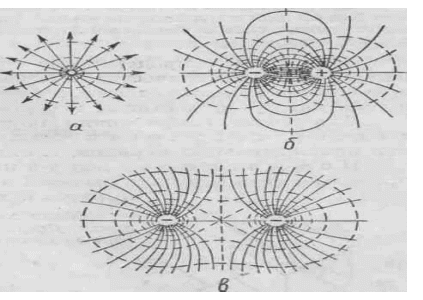
Рис. 6. Эквипотенциальные поверхности (пунктирные линии) и силовые линии (сплошные).

а — для точечного заряда; б — для двух разноименных численно равных зарядов;

в — для случая двух точечных одноименных зарядов.

На рис. 6,б изображены силовые линии и эквипотенциальные поверхности для двух точечных разноименных зарядов, равных по численному значению, а на рис. 6, в — для двух одноименно заряженных зарядов, численно равных.

Связь между напряженностью поля Е и потенциалом U. Существование такой связи следует из того факта, что работу электрических сил можно выразить через напряженность и разность потенциалов точек поля.

Рассмотрим однородное электростатическое поле напряженностью Е. Расстояние Δr (рис. 7) между эквипотенциальными поверхностями U₁ и U₂ бесконечно мало, следо­вательно, на всем расстоянии между ними можно считать напряженность поля Е постоянной.

Рис.7

Работа перемещения единичного заряда е на пути r₁ будет E r₁. Эта же работа может быть выражена через разность потенциалов начала U₂. и конца U₁. с обратным знаком:

, (4)

В неоднородном поле силовые линии не будут прямолинейными, а эквипотенциальные поверхности будут иметь сложную форму. Однако для бесконечно малых участков пространства можно пренебречь кривизной силовых линий и эквипотенциальных поверхностей и на основании предыдущих рассужде­ний записать:

(5)

Знак минус указывает, что напряженность Е направлена в ту сторону, в которую действует сила на положительный заряд, т. е. в сторону убывания потенциала.

Величина , характеризующая быстроту изменения потенциала при перемещении в направлении, перпендикулярном к эквипотенциальным поверхностям в сторону его увеличения, называется градиентом потенциала и обозначается grad U.

Как видно из (5), напряженность поля — это градиент потенциала с обратным знаком, т. е.

(6)