
- •1 Глоссарийлар
- •2 Дәріс оқулар
- •Туындыға қатысты шешілмеген теңдеуді параметр енгізу жолымен интегралдау
- •Лагранж және Клеро теңдеулері
- •Сызықтық бір тектес емес дифференциалдық теңдеуді тұрақтыны вариациялау әдісімен интегралдау
- •Шешімдердің түрлері және бірінші интеграл туралы түсінік
- •Дифференциалдық теңдеулердің қалыпты жүйесі
- •10. Эйлер әдісі.
- •Бірінші теңдеуді дифференциалдаймыз
- •3 Практикалық сабақтар
- •4 Студенттің оқытушы жетекшілігімен орындалатын өздік жұмысы
- •5 Емтиханға дайындық және өзін-өзі тексеруге арналған сұрақтар
- •1. Дифференциалдық теңдеулердің жалпы шешімін тап
- •2. Дифференциалдық теңдеулердің жалпы шешімін тап
- •3. Дифференциалдық теңдеулердің жалпы шешімін тап
- •4. Коши есебін шеш.
- •5. Коши есебін шеш.
- •6. Коши есебін шеш.
- •7. Дифференциалдық теңдеулердің жалпы шешімін тап.
- •8. Дифференциалдық теңдеулердің жалпы шешімін тап
- •9. Коши есебін шеш.
- •10. Дифференциалдық теңдеулердің жалпы шешімін тап
- •11. Дифференциалдық теңдеулердің жалпы шешімін тап
- •12. Дифференциалдық теңдеулердің жалпы шешімін тап
- •13. Дифференциалдық теңдеулердің жалпы шешімін тап
- •14. Коши есебін шеш.
- •6 Әдебиеттер
ПӘНДЕРДІҢ ОҚУ-ӘДІСТЕМЕЛІК КЕШЕНІ
«Дифференциалдық теңдеулер»
5B010900-Математика мамандығы үшін
ОҚУ -ӘДІСТЕМЕЛІК МАТЕРИАЛДАР
Семей
2014
МАЗМҰНЫ
Глоссарийлар.........................................................................................................3
Дәріс оқулар..........................................................................................................4
Практикалық сабақтар........................................................................................62
Студенттің өздік жұмысы ..................................................................................70
Емтиханға дайындық және өзін-өзі тексеруге арналған сұрақтар.................72
Әдебиеттер...........................................................................................................89
1 Глоссарийлар
№ |
Жаңа түсініктер |
Мағынасы |
1 |
|
Бірінші ретті дифференциалдық теңдеу |
2 |
M1(x)M2(y)dx+N1(x)N2(y)dy=0 |
Айнымалысы бөлектенетін дифференциалдық теңдеу |
3 |
|
Бірінші ретті біртектес дифференциалдық теңдеу |
4 |
|
Біртектес теңдеуге келтірілетін теңдеу. |
5 |
у'+p(x)y=q(x) |
Бірінші ретті сызықтық дифференциалдық теңдеу |
6 |
y'+p(x)y=y |
Бернулли теңдеуі |
7 |
|
F(x,y) -тің толық дифференциалы болу шарты |
8 |
(x,y)= |
Айнымалысы бөлектенетін теңдеудің интегралдық көбеткіші |
9 |
|
сызықтық теңдеудің интегралдық көбейткіші |
10 |
|
|
11 |
|
Лагранж теңдеуі |
12 |
|
Клеро теңдеуі |
13 |
|
жай дифференциалдық теңдеулер жүйесі |
14 |
|
|
15 |
|
Жаңа айнымалысын енгізіледі |
16 |
Тәуелсіз айнымалы болмайтын теңдеу
|
|
17 |
|
n ретті сызықтық біртектес дифференциалдық теңдеу |
18 |
|
n ретті сызықтық біртектес емес дифференциалдық теңдеу |
19 |
|
сызықтық дифференциалдық теңдеулердің қалыпты жүйесі |
2 Дәріс оқулар
ДӘРІС 1-2
Дәріс сабақтың құрылымы:
1 Дифференциалдық теңдеуге келтірілетін есептер
2 Жай дифференциалдық теңдеулер теориясы туралы негізгі ұғымдар
3 Бірінші ретті жай дифференциалдық теңдеулер
4 Айнымалысы бөлектенген теңдеулер
5 Айнымалысы бөлектенетін теңдеулер
Дәріс сабақтың мазмұны:
Зерттеліп отырған құбылысты немесе процесті сипаттайтын функцияны тікелей анықтау (табу) әлбетте, мүмкін болмайды. Алайда, тәуелсіз айнымалыны, функцияны, және олардың туындыларын байланыстыратын қатысты құрудың сәті түседі. Мұндай қатысты математикада дифференциалдық теңдеу деп атайды. Сонымен,
 ,
,
 (1)
(1)
түріндегі
теңдеуді (қатысты) дифференциалдық
теңдеу дейміз. Дифференциалдық теңдеуге
кіретін туындының ең жоғарғы реті
берілген дифференциалдық теңдеудің
реті деп аталады. Мысалға
 ,
,
 тиісінше бірінші, екінші ретті
дифференциалдық теңдеулер болады.
тиісінше бірінші, екінші ретті
дифференциалдық теңдеулер болады.
Анықтама:
Белгілі бір аралықта n
ретті үздіксіз дифференциалданатын
 функциясы
функциясы
 (1)
(1)
теңдеуді
х-ке
қарағанда тепе-теңдікке айналдырса,
демек
 болса, онда
болса, онда
 функциясы (1) теңдеудің шешімі деп
аталады. Мысалға,
функциясы (1) теңдеудің шешімі деп
аталады. Мысалға,
 теңдеуінің шешімі
теңдеуінің шешімі
 ,
ал
,
ал
 теңдеуінің шешімдері
теңдеуінің шешімдері
 немесе
немесе
 функциялары екені көрініп тұр. Сондай-ақ
функциялары екені көрініп тұр. Сондай-ақ
 функциясы екінші теңдеудің шешімі
екенін көрсетіңдер. Мұнда с1
,
с2
кез
келген еркін тұрақтылар.
функциясы екінші теңдеудің шешімі
екенін көрсетіңдер. Мұнда с1
,
с2
кез
келген еркін тұрақтылар.
Табиғаттану ғылымдарының, техниканың көптеген есептерін шешу дифференциалдық теңдеулерді құруға және оны шешуге келіп тіреледі.
Мысал-1. Кез келген нүктесінен жүргізілген жанаманың оу осінен қиып түсетін кесіндісінің шамасы жанасу нүктесінің екі еселенген ординатасына тең болатындай қисықтың теңдеуін тап.
М
іздеп отырған қисықтың кез келген
нүктесі болсын. М(х,у)
нүктесінен жүргізілген жанаманың
теңдеуі


![]() түрінде анықталатыны белгілі. Мұнда
X,Y
жанаманың ағымдағы координаттары,
түрінде анықталатыны белгілі. Мұнда
X,Y
жанаманың ағымдағы координаттары,
![]() -іздеп отырған функцияның берілген
нүктедегі туындысы. ОВ кесіндісінің
шамасын табу үшін х=0
деп аламыз.
-іздеп отырған функцияның берілген
нүктедегі туындысы. ОВ кесіндісінің
шамасын табу үшін х=0
деп аламыз.
Сонда
 болады. Екінші жағынан, есептің шарты
бойынша ОВ=2у.
Онда
болады. Екінші жағынан, есептің шарты
бойынша ОВ=2у.
Онда
 немесе
немесе
 теңдеуі іздеп отырған дифференциалдық
теңдеуіміз болып табылады. Оның шешімі
у=у(х)
жоғарыдағы есептің шартында көрсетілген
қасиеттерге ие болатын қисықтың теңдеуі
болып шығады.
теңдеуі іздеп отырған дифференциалдық
теңдеуіміз болып табылады. Оның шешімі
у=у(х)
жоғарыдағы есептің шартында көрсетілген
қасиеттерге ие болатын қисықтың теңдеуі
болып шығады.
Кіріспеде берілген есептердің шарты бойынша құрылған барлық дифференциалдық теңдеулерді осы курсты оқып үйрену барысында шеше алатын боласыңдар. Сөйтіп, есептерде қойылған сұрақтардың жауабын табуға да мүмкіндік туады.
F(x,y,y1)=0 (2)
түрінде
берілген теңдеуді бірінші ретті
дифференциалдық теңдеу деп атайды. Егер
(2) теңдеу
 -қа
қарағанда шешілетін болса, онда оны
-қа
қарағанда шешілетін болса, онда оны
=f(x,y) (3)
түріне келтіруге болады. (3) теңдеуді туындыға қатысты шешілген бірінші ретті дифференциалдық теңдеу деп атайды.
Анықтама
1.
Егер үздіксіз дифференциалданатын
y=(x)
функциясы
I
интервалында
(2) немесе (3) теңдеуді х
- ке қарағанда тепе-теңдікке айландырса,
демек F(x,
(x),
 (x))0
(
(x)f(x,
(x))),
кез келген хI,
онда (х)
функциясын берілген (2) немесе (3) теңдеудің
шешімі деп атайды.
(x))0
(
(x)f(x,
(x))),
кез келген хI,
онда (х)
функциясын берілген (2) немесе (3) теңдеудің
шешімі деп атайды.
Егер ф(х,у)=0 теңдеуі у-ті х-тің функциясы ретінде анықтайтын болса, (y=(x)) және (x) функциясы (3) теңдеудің шешімі болса, онда ф(х,у)=0 қатысын (3) теңдеудің айқындалмаған формадағы шешімі (интегралы) деп атайды.
Мысалы-2.
Айталық
 теңдеуі берілсін функция y=eх
осы теңдеудің шешімі болады. Себебі
теңдеуі берілсін функция y=eх
осы теңдеудің шешімі болады. Себебі
eхlneх –xeх=eхx-xeх0 .
Алайда, берілген теңдеудің басқада шешімдері бар. Мысалы, e-х функциясы да осы теңдеудің шешімі болады.
е-хlne-х-x(e-х)1=e-х(-x)-xe-х(-1)0
Сондай-ақ есх түріндегі функцияларда (мұнда с-қандайда бір тұрақты) берілген теңдеудің шешімі болатының тексеруге болады.
Сонымен дифференциалдық теңдеудің бір шешімі ғана емес, көп шешімі болатынына көзімізді жеткіздік. Бұл факт, тіпті интегралдық есептеу кезінен белгілі болған. Шынында да,
 (4)
(4)
қарапайым теңдеуін алсақ, бұл теңдеудің шешімі f(x) функциясының анықталмаған интегралы екені белгілі.


Демек, сансыз көп шешімі бар. (4) теңдеудің шешімдерінің жалпы түрін былай жазуға болады. у=(x)+c мұнда (х) (4) теңдеудің қандайда бір шешімі. С-ға мәндер беру арқылы (4) теңдеудің дербес шешімін табуға болады.
(3) дифференциалдық теңдеудің шешімдерінің жалпы түрін у=(x,с) формуласы арқылы жазуға болады.
Жалпы жағдайда дифференциалдық теңдеулердің шешімдерінің жалпы түрі Ф(х,у,с)=0 формуласы арқылы жазылады. Бұл қатысты (3) теңдеудің жалпы интегралы деп атайды.
(3) теңдеудің шешімінің графигін осы теңдеудің интегралдық қисығы деп атайды. Жоғарыда айтылғандай кез келген дифференциалдық теңдеудің шешімдері ақырсыз жиын болатынын айттық. Практикада дифференциалдық теңдеудің белгілі шартты қанағаттандыратындай бір ғана шешімін табу керек болады.
(3)
теңдеудің (х0)=у0
(
y| )
шартын қанағаттандыратын у=(х)
шешімін табуды
)
шартын қанағаттандыратын у=(х)
шешімін табуды
 теңдеуі үшін тұжырымдалған Коши есебі
(немесе бастапқы есеп) дейді.
теңдеуі үшін тұжырымдалған Коши есебі
(немесе бастапқы есеп) дейді.
y|
шартын бастапқы шарт деп атайды. х0,,
у0
 шамаларын
бастапқы берілімдер дейді.
шамаларын
бастапқы берілімдер дейді.
 функциясы белгілі шарттарды
қанағаттандырғанда
функциясы белгілі шарттарды
қанағаттандырғанда
 теңдеуі
үшін тұжырымдалған Коши есебінің жалғыз
ғана шешімінің бар және жалғыз болатынын
дәлелдеуге болады.
теңдеуі
үшін тұжырымдалған Коши есебінің жалғыз
ғана шешімінің бар және жалғыз болатынын
дәлелдеуге болады.
 (5)
(5)
теңдеуін әрқашан
M(x,y)dx+N(x,y)dy (6)
түріне келтіруге болады және керісінше. Мысалға (5) теңдеуді (1.12) теңдеуге келтіру үшін оның екі жағын N(x,y)dx көбейтсек болғаны. Сонда (6) түрге келтіреміз. Бұл жағдайда M(x,y)=-f(x,y)N(x,y).
Анықтама
5.
Мына түрдегі
 (1.11/)
және M1(x)M2(y)dx+N1(x)N2(y)dy=0
(7) теңдеулерді айнымалысы
ажыратылатын теңдеу деп атаймыз. (7)
теңдеуіне тән қасиет dx
пен dy
шамаларының коэффицеттері екі функцияның
көбейтіндісінен тұрады. Олардың әрқайсысы
бір ғана айнымалыға тәуелді болады.
(1.11/)
және M1(x)M2(y)dx+N1(x)N2(y)dy=0
(7) теңдеулерді айнымалысы
ажыратылатын теңдеу деп атаймыз. (7)
теңдеуіне тән қасиет dx
пен dy
шамаларының коэффицеттері екі функцияның
көбейтіндісінен тұрады. Олардың әрқайсысы
бір ғана айнымалыға тәуелді болады.
Егер
 болса,
онда (7)
теңдеуді
болса,
онда (7)
теңдеуді
 түріне келтіреміз. Соңғы теңдеуді мына
түрде жазуға болады:
түріне келтіреміз. Соңғы теңдеуді мына
түрде жазуға болады:

Осыдан

Мұнда C еркін тұрақты. Алынған теңдеудің сол жағын F(x,y) белгілесек F(x,y)=C теңдігін аламыз. Ол берілген теңдеудің жалпы интегралы болып табылатыны белгілі.
Ал
егер
 ,
онда
y=y0
функциясы
(7)
теңдеуінің
шешімі
болады.
Өйткені
(7)
теңдеуінің
dy=dy0=0
болғандықтан
екінші
қосылғышы
да
нольге
айналады.
Сондай-ақ
N1,(x0)=0,
онда
x=x0
де
(7)
теңдеуінің
шешімі
болады.
Дәлелдеу
жоғарғыдай.
,
онда
y=y0
функциясы
(7)
теңдеуінің
шешімі
болады.
Өйткені
(7)
теңдеуінің
dy=dy0=0
болғандықтан
екінші
қосылғышы
да
нольге
айналады.
Сондай-ақ
N1,(x0)=0,
онда
x=x0
де
(7)
теңдеуінің
шешімі
болады.
Дәлелдеу
жоғарғыдай.
Бұл шешімдер дербес немесе ерекше шешімде бола алады. Егер көрсетілген шешімдер параметр C–ның белгілі бір мәндерінде жалпы шешімінен алынса, онда олар дербес шешімдер болады, ал қарама-қарсы жағдайда ерекше шешімге жатады.
Мысал-3..
 .
Бұл
теңдеудің
айнымалысы
ажыратылған.
Сондықтан
.
Бұл
теңдеудің
айнымалысы
ажыратылған.
Сондықтан
 интегралдау
арқылы
интегралдау
арқылы
 аламыз.
Осыдан
аламыз.
Осыдан
 немесе
немесе
 ,
,
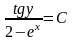 ,
мұнда
,
мұнда
 немесе
немесе
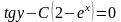 .
.
Мысал-4. Теңдеудің дербес шешімдерін тап немесе Коши есебін шеш.

Алдымен жалпы шешімді іздейміз

Берілген
теңдеу
айнымалысы
ажыратылатын
теңдеу.
Онда
 интегралдасақ
интегралдасақ
 .
.
Потенциалдағаннан
кейін
 ,
немесе
,
немесе
 болады.
Сонымен жалпы шешім табылды. Жалпы
шешімнен дербес шешімді бөліп алу үшін
болады.
Сонымен жалпы шешім табылды. Жалпы
шешімнен дербес шешімді бөліп алу үшін
 ,
деп алып, демек
,
деп алып, демек
 ,e=ec
,e=ec
 c=1
Cонда
іздеп отырған дербес шешім
c=1
Cонда
іздеп отырған дербес шешім
 функциясы
болады.
функциясы
болады.
 теңдеуі
айнымалысы ажыратылатын теңдеуге
келтіріледі. Ол үшін ax+by+c=z
деп аламыз.
теңдеуі
айнымалысы ажыратылатын теңдеуге
келтіріледі. Ол үшін ax+by+c=z
деп аламыз.

 .
ax+by+c
және
.
ax+by+c
және
 ауыстыру арқылы
ауыстыру арқылы
 теңдеуін
аламыз. Бұл теңдеу-айнымалысы ажыратылатын
теңдеу. Оны интегралдау арқылы Ф(х,z,c1)=0
теңдігіне келеміз. Енді z–ті
ax+by+c
өрнегімен ауыстырып Ф(х,ах+ву+с,c1)=0
немесе F(x,y,c1)=0
жалпы шешімі (жалпы интегралы) табылады.
теңдеуін
аламыз. Бұл теңдеу-айнымалысы ажыратылатын
теңдеу. Оны интегралдау арқылы Ф(х,z,c1)=0
теңдігіне келеміз. Енді z–ті
ax+by+c
өрнегімен ауыстырып Ф(х,ах+ву+с,c1)=0
немесе F(x,y,c1)=0
жалпы шешімі (жалпы интегралы) табылады.
Өзін-өзі тексеруге арналған сұрақтар:
1 Жай дифференциалдық теңдеулер теориясы туралы негізгі ұғымдар
2 Бірінші ретті жай дифференциалдық теңдеулер
3 Айнымалысы бөлектенетін теңдеулер
Қолданылған әдебиеттер:
1. Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные уравнения.- М.: Наука, 1985
2. Қалиев С.Қ., Искакова М.Т. Дифференциалдық теңдеулер және варияциялық есептеу негіздері, Семей – 2005
3. Филлипов А.Ф. Сборник задач по обыкновенные дифференциальным уравнениям. М.: Наука, 1984
4. Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. - Москва.: Изд-во МГУ, 1984.
5. Қадыкенов Б.М. Дифференциалдық теңдеулердің есептері мен жаттығулары Алматы: Қазақ университеті, 2002
ДӘРІС 3-4
Дәріс сабақтың құрылымы:
1 Біртектес теңдеулер
2 І-ретті сызықтық дифференциалдық теңдеулер
3 Бернулли теңдеуі
4 Толық дифференциалдағы теңдеулер. Интегралдаушы көбейткіш
Дәріс сабақтың мазмұны:
Анықтама
6.
Егер кез келген к
үшін
 теңдігі
орындалса, онда
теңдігі
орындалса, онда
 функциясын
m
дәрежелі біртектес функция деп атайды.
функциясын
m
дәрежелі біртектес функция деп атайды.
Мысалға,
 функциясы үш дәрежелі біртектес функция,
өйткені
функциясы үш дәрежелі біртектес функция,
өйткені
 .
.
 функциясы «0» дәрежелі біртектес функция,
себебі кез келген
функциясы «0» дәрежелі біртектес функция,
себебі кез келген
 . “0” дәрежелі біртектес функцияны
. “0” дәрежелі біртектес функцияны
 қатынасының функциясы ретінде өрнектеуге
болатынын көрсетейік.
қатынасының функциясы ретінде өрнектеуге
болатынын көрсетейік.
Айталық,
 “0” дәрежелі біртектес функция болсын.
“0” дәрежелі біртектес функция болсын.
 деп
алайық. Сонда анықтама бойынша
деп
алайық. Сонда анықтама бойынша
 (8)
(8)
Айталық,
функциясы
m
дәрежелі
біртектес
функция
болсын.
Онда
 функциясы
“0” дәрежелі
біртектес
функция
болатыны
көрінеді.
Онда
жоғарыдағы
тұжырымның
негізінде
функциясы
“0” дәрежелі
біртектес
функция
болатыны
көрінеді.
Онда
жоғарыдағы
тұжырымның
негізінде
 ,
осыдан
,
осыдан
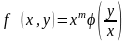 .
Бұл
өрнектеу
m
дәрежелі
біртектес
функцияның
жалпы
түрі
болып
табылады.
.
Бұл
өрнектеу
m
дәрежелі
біртектес
функцияның
жалпы
түрі
болып
табылады.
Анықтама
7.
Егер
 және
және
 функциялары
бірдей
дәрежелі
біртектес
функциялар
болса,
онда
теңдеуі
бірінші
ретті
біртектес
теңдеу
деп
аталады.
функциялары
бірдей
дәрежелі
біртектес
функциялар
болса,
онда
теңдеуі
бірінші
ретті
біртектес
теңдеу
деп
аталады.
Біртектес
теңдеулер
 (немесе
(немесе
 )
алмастыруы
арқылы
айнымалысы
ажыратылатын
теңдеуге
келтіріледі.
Шынында
да
(6)
теңдіктің
көмегімен
(8)
теңдеуді
былай
түрлендіреміз:
)
алмастыруы
арқылы
айнымалысы
ажыратылатын
теңдеуге
келтіріледі.
Шынында
да
(6)
теңдіктің
көмегімен
(8)
теңдеуді
былай
түрлендіреміз:

 болғандықтан,
қысқарту
арқылы
болғандықтан,
қысқарту
арқылы теңдеуін
аламыз.
десек,
осыдан,
теңдеуін
аламыз.
десек,
осыдан,
 .
Осыларды
соңғы
теңдеуге
апарып
қойсақ
.
Осыларды
соңғы
теңдеуге
апарып
қойсақ
 теңдеуін
аламыз,
немесе
теңдеуін
аламыз,
немесе
 .
Сөйтіп,
айнымалысы
ажыратылатын
теңдеуге
келтірдік.
.
Сөйтіп,
айнымалысы
ажыратылатын
теңдеуге
келтірдік.
Енді
айнымалысын
ажырату
арқылы
 теңдеуіне
келеміз.
Осыдан
теңдеуіне
келеміз.
Осыдан
 .
Потенциалдау
арқылы
мына
түрде
жазамыз,
.
Потенциалдау
арқылы
мына
түрде
жазамыз,
 немесе
немесе
 -бұл
соңғы
нәтиже.
-бұл
соңғы
нәтиже.
Біртектес теңдеудің интегралдық қисықтары бір-біріне ұқсас болады. Ұқсастық центрі координаттың бас нүктесінде орналасқан.
Мысал-4.
 теңдеуін
шеш.
Мұнда
теңдеуін
шеш.
Мұнда
 .
Бұл
функциялар
екінші
ретті
біртектес
функциялар.
Ендеше
берілген
теңдеу
біртектес
теңдеу
болады.
.
Бұл
функциялар
екінші
ретті
біртектес
функциялар.
Ендеше
берілген
теңдеу
біртектес
теңдеу
болады.
 деп
алып
деп
алып
 және
және
 шамаларын
ауыстырамыз
(алмастырамыз)
шамаларын
ауыстырамыз
(алмастырамыз)





интегралдау
арқылы
 .
.
Потенциалдап теңдігін аламыз.
теңдігін аламыз.
 -ны
-ны
 -ке
ауыстырсақ
-ке
ауыстырсақ
 .
.
Әрі
қарай түрлендірсек
 .
.
Бұл
теңдеу центрі
 нүктeсінде,
ал радиусы
нүктeсінде,
ал радиусы
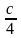 -ке
тең болатын шеңберлер үйірі болып
табылады.
-ке
тең болатын шеңберлер үйірі болып
табылады.
теңдеуін
қарастырайық. Бұл теңдеу біртектес
теңдеуге келтірілетін теңдеу. Мұнда
 –тұрақтылар,
ал
–тұрақтылар,
ал
 –функциясы
өзінің аргументі бойынша үзіліссіз
функция. Егер
–функциясы
өзінің аргументі бойынша үзіліссіз
функция. Егер
 болса берілген теңдеу біртектес болатыны
көрініп тұр. Сондықтан
болса берілген теңдеу біртектес болатыны
көрініп тұр. Сондықтан
 мен
мен
 -дің
кемінде біреуі нольден өзгеше болады
деп есептейміз.
-дің
кемінде біреуі нольден өзгеше болады
деп есептейміз.
Екі жағдайды айырып қараймыз.
10.
 ,
осы жағдайда
,
осы жағдайда
 ауыстырымын
енгізу арқылы берілген теңдеуді біртектес
теңдеуге келтіруге болады. Мұнда
ауыстырымын
енгізу арқылы берілген теңдеуді біртектес
теңдеуге келтіруге болады. Мұнда

 (*)
(*)
теңдеулер
жүйесінің шешімі. Енді x,y
және y/-ты
жаңа айнымалылармен ауыстыру арқылы
берілген теңдеу

теңдеуіне түрленеді. Ал соңғы теңдеу біртектес, оның шешімін табуды білеміз.
20. . Бұл жағдайда (*) системасының жалпы алғанда шешімі болмайды.
Егер
 деп
алсақ, берілген теңдеу айнымалысы
ажыратылатын теңдеуге айналады.
деп
алсақ, берілген теңдеу айнымалысы
ажыратылатын теңдеуге айналады.
Мысал-5.
 теңдеуін шеш.
теңдеуін шеш.
 -ты
пен
ауыстырып,
-ты
пен
ауыстырып,
 теңдікке
келеміз.
теңдікке
келеміз.
 системасын құрамыз. Системаның
анықтауышы:
системасын құрамыз. Системаның
анықтауышы:

Системаның
жалғыз ғана шешімі болады, демек,
 .
.
x
және y
айнымалыларының
орнына жаңа айнымалылар s
пен r-ді
төмендегі қатыс арқылы енгіземіз.
 осыдан
осыдан

x,
y,
-ті
жаңа айнымалылар арқылы ауыстырсақ
 біртектес теңдеу шығады. Әрі қарай,
біртектес теңдеу шығады. Әрі қарай,
 айнымалысын енгізіп, теңдеуді шешеміз,
нәтижесінде
айнымалысын енгізіп, теңдеуді шешеміз,
нәтижесінде
 теңдігін аламыз. (түрлендірулерді
өздерің жүргізіңдер).
теңдігін аламыз. (түрлендірулерді
өздерің жүргізіңдер).
Ақырында
r,s
айнымалыларын
ескі x
пен y
айнымалылары арқылы өрнектен
 жалпы интегралды табамыз.
жалпы интегралды табамыз.
Анықтама 8.
у'+p(x)y=q(x) (9)
түріндегі теңдеуді бірінші ретті сызықтық дифференциалдық теңдеу деп атайды.
Мұнда р(х),g(х) үздіксіз функциялар.
Байқасаңдар, у' туындысы функция у-тің сызықтық функциясы. Сондықтан да сызықтық теңдеу деп аталған.
Егер
g(x) 0
-са, онда (9) теңдеу
айнымалысы ажыратылатын теңдеуге
айналады. Жалпы жағдайда (9) теңдеудің
айнымалысы ажыратылмайды.
0
-са, онда (9) теңдеу
айнымалысы ажыратылатын теңдеуге
айналады. Жалпы жағдайда (9) теңдеудің
айнымалысы ажыратылмайды.
Сондықтан (9) теңдеудің өзіне тән шығару әдісін көрсетеміз. Ол үшін белгісіз функцияны у=uv (*) түрінде іздейміз, мұнда u(x) және v(x) дифференциялданатын функциялар.Туындыны табамыз.
у'=u'v+uv'
Енді осы өрнектерді (9) теңдеуге қойып, оны мына түрге келтіруге болады.
u'v+u(v'+p(x))=q(x) (10)
v-функциясын v'+p(x)v өрнегін x-ке қарағанда тепе–теңдікке айландыратындай етіп таңдап аламыз. Ондай функция
v'+p(x)v=0 (11)
теңдеудің шешімі бола алады.
(11)- теңдеудің бір ғана шешімін табу жеткілікті .
Мысалға, ондай шешім:
 (12)
(12)
болады.
Ал у=uv функциясы (10) теңдеудің шешімі болу үшін u-функциясы u'v0(x)=q(x) немесе
 (13)
(13)
теңдеуінің шешімі болуға тиіс. (1.18) теңдеуді шешеміз


Енді v және u фунцияларының өрнегін (*) теңдікке апарып қойсақ,
 (14)
(14)
іздеп отырған шешімді табамыз. (1.19)-формуланы мына түрде де
 (15)
(15)
жазуға болады.
Бірақ бұл жағдайда формулаға кіретін әрбір анықталмаған интегралды бір ғана алғашқы функция ретінде қарастырған жөн болады.
(14) немесе (15) формулаларын осылай қорыту әдісін Бернулли әдісі деп атайды.
Сөйтіп сызықтық теңдеуді шешу ( шығару) үшін қорытылған (14) немесе (15) формулаларын пайдалануға болады. Алайда Бернулли әдісін әрбір теңдеуге тікелей қолдану арқылы да шешеді.
Бернулли әдісін көрсету барысында байқағанымыздай сызықтық теңдеудің шешімін табу төмендегі дифференциалды теңдеулер системасына келіп тіреледі.
 (16)
(16)
Системаны құрайтын теңдеулердің екеуі де айнымалысы ажыратылатын теңдеулер. Біріншісін шешіп v функциясын табамыз. Табылған функцияны екіншісіне қойып u функциясын анықтаймыз. Соңында
y=u·v
түріндегі берілген сызықтық теңдеуінің шешімі табылады.
Мысал-6. y'+3y=e2х мұнда р(x)=3, q(x)=e2х. (15) формуласын пайдаланып шешейік.
y=e (
( 2x·e
2x·e dx+C)=e-3x(
2x·e3xdx+c)=e-3x(1/5e5x+C)
dx+C)=e-3x(
2x·e3xdx+c)=e-3x(1/5e5x+C)
Сөйтіп,
y= e2x+Ce-3x
e2x+Ce-3x
Мысал-7.
y'+2xy=xe-x -теңдеуінің
жалпы шешімін табу керек .
-теңдеуінің
жалпы шешімін табу керек .
Мұнда p(x)=2x, q(x)=xe-x
Бұл теңдеуді (16) ситеманы құру арқылы шығарайық.

Бірінші теңдеудің бір ғана шешімі жеткілікті.
 =-2xdx,
lnv=-x2
v=e-x
=-2xdx,
lnv=-x2
v=e-x
Екінші теңдеуге v функциясының өрнегін қойып, оны шешеміз.
u/e-x =xe-x , u/=x u=x2/2+C
Сөйтіп, берілген теңдеудің жалпы шешімі y= e-x (x2/2+C ) функциясы.
Анықтама 9.
y'+p(x)y=y q(x) (17)
теңдеуді Бернулли теңдеуі дейді. Мұнда кез келген нақты сан .
Егер
=0
–болса, онда (17) теңдеу сызықтық теңдеуге,
ал
=1 болса, айнымалысы ажыратылатын
теңдеуге айналады. Сондықтан
 0,1
деп есептейміз.
0,1
деп есептейміз.
Бернулли теңдеуі сызықтық теңдеуге келтірілетін теңдеуге жатады.
Егер (17) теңдеудің екі жағын y бөлсек, онда
y- y'+p(x)y1- =q(x) (18)
теңдеуін аламыз. z=y1- десек, z'=y- y'(1- )
Сонда
y-
y'= . Енді (18) теңдеуге қойсақ,
. Енді (18) теңдеуге қойсақ,
 (19)
(19)
теңдеуі шығады. (19) теңдеудің z айнымалысына қарағанда сызықтық екені көрініп тұр. (17) теңдеудің де шешімін y=u·v түрінде іздейміз. Бернулли әдісі бойынша теңдеуді түрлендіріп
 (20)
системасын алуға болады. Бірінші теңдеуді
шешіп v
-ны, екінші теңдеуді шешіп u–ды
табамыз.
(20)
системасын алуға болады. Бірінші теңдеуді
шешіп v
-ны, екінші теңдеуді шешіп u–ды
табамыз.
Мысал-8. y'+y/x=-2x2y2 теңдеуінің жалпы шешімін тап.
p(x)=1/x, q(x)=-2x2 , =2
(24) системаны құрамыз: y=u·v

Бірінші
теңдеуді шешсек
 ,
,
 ,
,

 ,
,
 ;
;
 ;
;

F(x,y) eкі айнымалы функцияның толық дифференциалы
dF(x,y)= dx+
dx+ dy
dy
түрінде анықталатыны белгілі.
Егер
M(x,y)dx+N(x,y)dy (21)
өрнегі берілсе, онда (21) өрнек қай жағдайда қандайда бір функцияның толық дифференциалы болады деген табиғи сұрақ өзінен-өзі туады. Басқаша айтсақ,
=M(x,y)
және
 =N(x,y)
=N(x,y)
теңдіктері орындалатындай F(x,y) функциясы бар болатынын қалай білуге болады деген сөз.
Бұл сұраққа төменде дәлелденетін теорема жауап береді. Біз былайғы жерде M(x,y) және N(x,y) функцияларының белгілі бір D облыста үзіліссіз дербес туындылары бар деп есептейміз.
Теорема 2 (21) өрнек D облыста анықталған екі айнымалы функциясы F(x,y) -тің толық дифференциалы болу үшін
= (22)
теңдігінің осы D облысында орындалуы қажетті және жеткілікті .
Дәлелдеуі 1) Алдымен (22) шарттың қажеттілігін дәлелдейік.
Ол үшін (21) өрнек қандайда бір F(x,y) функциясының D облысында толық диффернциалы деп жорыйық, демек
M(x,y) dx+N(x,y) dy =dF(x,y)
Бұл жағдайда =M(x,y) және =N(x,y) болатыны белгілі. M(x,y) және N(x,y) функцияларының дербес туындысын табайық.
 және
және
 (23)
(23)
Шарт бойынша және D облысында үзіліссіз. Ендеше екінші ретті аралас туындылар
 және
және

D облысында үзіліссіз болады.
Анализден белгілі теорема бойынша
=
,
 .
Осыдан
.
Осыдан
 теңдігі шығады
теңдігі шығады
(22) шарттың жеткіліктігін дәлелдейік.
Айталық, = , . Осы жағдайда (21) өрнек қандайда бір функцияның толық дифференциалы болатынын көрсетейік. Ол үшін
F(x,y)= +
+ (24)
(24)
деп белгілейік. Мұнда әзірше белгісіз функция. (24) формуладан
=M(x,y), (25)
болатынын көреміз.
Eнді
=N(x,y) (26)
болатындай етіп, функциясын табамыз. (24) теңдікті y айнымалысы бойынша дифференциалдап (26) теңдікті мына түрде
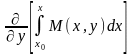 +
+ =
N(x,y) (27)
=
N(x,y) (27)
жазамыз.
М(x,y)
және
үзіліссіз функциялар болғандықтан
(27) теңдікті мына түрде
 +
=N(x,y)
жазуға болады. Соңғы теңдіктен
-ті
табамыз.
+
=N(x,y)
жазуға болады. Соңғы теңдіктен
-ті
табамыз.
= N(x,y) - (28)
Егер (28) теңдіктің оң жағы x-ке тәуелсіз болса, онда іздеп отырған функциямыз -ті (28) теңдіктің екі жағын интегралдау арқылы тауып аламыз.
Шынында да, (28) теңдіктің оң жағы x-ке тәуелсіз екенін (22) теңдіктің негізінде көрсетейік:

Демек, (28) теңдіктің оң жағы x- ке тәуелсіз. Енді (28) және (26) теңдіктердің негізінде
dF(x,y) = dx+ dy= M(x,y) dx +N(x,y) dy ,
екенін көреміз.
Анықтама 10. Егер
M(x,y) dx +N(x,y) dy =0 (29)
теңдеуінің сол жағы екі айнымалы функциясының толық дифференциалы болса, онда (29) теңдеуді толық дифференциал теңдеу дейміз.
Анықтамада айтылған функцияны F(x,y) деп белгілесек, (29) теңдеуді былай жазуға болады. dF(x,y)=0
Бұл теңдеудің шешімі F(x,y)=C болатыны белгілі. Осыдан толық дифференциал теңдеуді шешу, ол теңдеудің оң жағының толық дифференциалы болатын функцияны табуға келіп тіреледі екен.
Мұндай функция жоғарыдағы дәлелденген теореманың дәлелдеу жолы бойынша табылады.Оны төмендегі мысалмен көрсетеміз.
Мысал-9. (6 x2 y2 + 6 xy –1) dx +(4 x3 y +3 x2 +2 y ) dy=0
теңдеуінің жалпы шешімін тап.
M(x,y) =6 x2 y2 + 6 xy –1 , N(x,y) =4 x3 y +3 x2 +2 y
Берілген теңдеудің толық дифференциaл теңдеу екенін тексереміз, демек
= көрсетеміз.
=12 x2 y + 6 x
=12
x2
y + 6 x

Осыдан толық дифференциал теңдеу екені шығады. (24) формулада интеграл шегі x0 -ді кез келген жолмен таңдап алатын болғандықтан, демек (24) формула М(х,у) функциясының кез келген алғашқы функциясы үшін орындалатындықтан анықталған интегралдың орнына сәйкес анықталмаған интегралды жазсақ та болады.
Сонымен,
F(x,y)
= (6
x2
y2
+ 6 xy –1)dx +
=
2 x 3y2
+ 3 x 2y
– x +
(*)
(6
x2
y2
+ 6 xy –1)dx +
=
2 x 3y2
+ 3 x 2y
– x +
(*)
-ті табу үшін ( 1.31) формуланы пайдаланамыз.
4 x3 y +3 x2+ =4 x3 y +3 x2 +2 y
Осыдан =2y =y2+C1
Енді (*) теңдіктегі -тің орнына қойып
F(x,y)= 2 x 3y2 + 3 x 2y – x+ y2+C1
теңдігін аламыз.
Жалпы шешім
2 x 3y2 + 3 x 2y – x+ y2+C1 =C2 немесе 2 x 3y2 + 3 x 2y – x+ y2=C
Айталық,
P(x,y) dx +Q(x,y) dy =0 (30)
теңдеу толық дифференциал теңдеу болмасын, алайда осы теңдеуді бір (x,y) функциясына көбейткеннен шыққан теңдеу.
M(x,y) dx +N (x,y) dy =0 , M(x,y) =p(x,y) (x,y)
N (x,y)= Q(x,y) (x,y) ; толық дифференциал теңдеу болып шықса,
(x,y) функциясын (30) теңдеудің интегралдаушы көбейткіші деп атайды.
Мысалға, M1(x) M2(y) dx +N1(x) N2(y) dy=0
айнымалысы ажыратылатын теңдеудің интегралдық көбеткіші (x,y)= функциясы болады. Демек осы көбейткішке көбейткеннен шыққан теңдеу толық дифференциал теңдеу болады. (өздерің дәлелдеңдер)
Сондай-ақ yp(x)y = q(x) сызықтық теңдеудің интегралдық көбейткіші функциясы болатынын көрсету қиын емес.
Сөйтіп, біз бұрынырақ қарастырған теңдеулерді толық дифференциал теңдеуге келтіру арқылы шығаруға болады екен.
Тағы
бір ескертетін жағдай бір ғана
дифференциалдық теңдеу үшін бірнеше
интегралдық көбейткіш бар болуы мүмкін.
Мысалға 2ydx +xdy=0
теңдеуін алайық. Осы теңдеу үшін 1
(x,y)=x, 2
(x,y) = ,
3(x,y)
,
3(x,y)
 функциялары интегралдық көбейткіштер
болады. (Осыны дәлелдеңдер)
функциялары интегралдық көбейткіштер
болады. (Осыны дәлелдеңдер)
Өкінішке орай, кез келген теңдеу үшін интегралдық көбейткіштерді табудың ортақ әдісі жоқ. Кейбір дербес теңдеулер үшін интегралдық көбейткіш табудың дербес әдістері бар.
Өзін-өзі тексеруге арналған сұрақтар:
1 Біртектес теңдеулер
2 Сызықтық теңдеулер
3 Бернулли теңдеуі
4 Толық дифференциалдағы теңдеулер
Қолданылған әдебиеттер:
1. Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные уравнения.- М.: Наука, 1985
2. Қалиев С.Қ., Искакова М.Т. Дифференциалдық теңдеулер және варияциялық есептеу негіздері, Семей – 2005
3. Филлипов А.Ф. Сборник задач по обыкновенные дифференциальным уравнениям. М.: Наука, 1984
4. Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. - Москва.: Изд-во МГУ, 1984.
5. Қадыкенов Б.М. Дифференциалдық теңдеулердің есептері мен жаттығулары Алматы: Қазақ университеті, 2002
ДӘРІС 5-7
Дәріс сабақтың құрылымы:
1 Коши есебі. Пикар теоремасы
2 Параметрге және бастапқы шартқа үзіліссіз тәуелді шешілу туралы теорема
3 Туындыға қатысты шешілмеген теңдеу.
4 Ерекше шешімдер туралы түсінік, Клеро және Лагранж теңдеулері
Дәріс сабақтың мазмұны:
(1)
түріндегі теңдеу туындыға қатысты шешілмеген бірінші ретті дифференциалдық теңдеу деп аталады. Ең алдымен осы теңдеудің шешімдерінің бар болуының жеткілікті шарттарын анықтаумен айналысамыз.
Айталық (1) теңдеуді -қа қатысты шешудің сәті түсті деп жорыйық. Онда бір немесе бірнеше, туындыға қатысты шешілген теңдеулер алуымыз мүмкін:
 (k=1,2,,..)
(2)
(k=1,2,,..)
(2)
Айталық
функциялар
 (k=1,2,..)
жазықтықтықта
(k=1,2,..)
жазықтықтықта
 нүктесінің төңірегінде Пикар теоремасының
шарттарын қанағаттандырсын. Онда
нүктесі арқылы бір-бірден
нүктесінің төңірегінде Пикар теоремасының
шарттарын қанағаттандырсын. Онда
нүктесі арқылы бір-бірден
 интегралдық қисықтары (1) теңдеудің
шешімдері екені белгілі және
интегралдық қисықтары (1) теңдеудің
шешімдері екені белгілі және
 (k=1,2,..)
интегралдық қисығына
нүктесінде жүргізілген жанама векторының
бағыты
(k=1,2,..)
интегралдық қисығына
нүктесінде жүргізілген жанама векторының
бағыты
 мәнімен анықталады. Егер
(k=1,2,.)
мәндері әр түрлі болса, онда
нүктесінен әр түрлі интегралдық қисықтар
өтеді. Ал
мәнімен анықталады. Егер
(k=1,2,.)
мәндері әр түрлі болса, онда
нүктесінен әр түрлі интегралдық қисықтар
өтеді. Ал
 нүктесінен жүргізілген жанама векторлар
да әртүрлі болғандықтан (1)
нүктесінен жүргізілген жанама векторлар
да әртүрлі болғандықтан (1) теңдеудің
белгілі-бір шешімін бөліп алу үшін
теңдеудің
белгілі-бір шешімін бөліп алу үшін
 бастапқы
шарттармен бірге
бастапқы
шарттармен бірге
 шарты қоса берілуге тиіс. Көріп
отырғанымыздай y0/
мәні қалай болса солай беріле салмайды.
шарты қоса берілуге тиіс. Көріп
отырғанымыздай y0/
мәні қалай болса солай беріле салмайды.
 мәні
мәні
 (3)
(3)
теңдеуінің түбірі болуға тиіс.
Сөйтіп, (1) теңдеудің шешімінің бар болуы біріншіден, оның –қа қатысты шешілу мүмкіндігімен екіншіден, (2) теңдеудің шешімдерінің бар болуымен байланысты екен.
Теорема
3. Егер центрі ( )
нүктесінде (
,
F(
)
нүктесінде (
,
F( )=0
теңдеудің түбірі) болатын
)=0
теңдеудің түбірі) болатын
 тұйық параллелепипедінде мына шарттар
тұйық параллелепипедінде мына шарттар
а) функция
F( )
өзінің дербес тундылары
)
өзінің дербес тундылары
 және
және
 пен бірге аргументтерінің жиынтығы
бойынша үзіліссіз.
пен бірге аргументтерінің жиынтығы
бойынша үзіліссіз.
б)
 (
( )
0
орындалса, онда
)
0
орындалса, онда
 нүктесінің
белгілі бір төңірегінде
нүктесінің
белгілі бір төңірегінде
 (4)
(4)
шартттарын қанағаттандыратын (1) теңдеудің шешімі бар болады.
Дәлелдеу.
Теореманың а) және б) шарттарының
негізінде ( )
нүктесінің төңірегінде
)
нүктесінің төңірегінде
 айқындалмаған функциясының бар және
жалғыз болу шарттары орындалады. Оның
үстіне, центрі (
айқындалмаған функциясының бар және
жалғыз болу шарттары орындалады. Оның
үстіне, центрі ( )
нүктесінде болатын D2
тіктөртбұрышы табылып,
сол D2
-да f(x,y)
функциясы
)
нүктесінде болатын D2
тіктөртбұрышы табылып,
сол D2
-да f(x,y)
функциясы
 дербес туындысымен бірге үзіліссізболады.
дербес туындысымен бірге үзіліссізболады.

Демек,
 бастапқы есебінің
бастапқы есебінің
 сегментінде жалғыз ғана шешімі болады.
сегментінде жалғыз ғана шешімі болады.
Егер (2) теңдеулердің интегралдық қисықтары ( ) нүктесінен өтетін болса және олардың осы нүктеден жүргізілген ортақ жанамасы болса, онда ( ) нүктесінде көрсетілген теореманың шарттары орындалмайды.

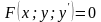


 q(x)
q(x) =
=



 ші
ретті дифференциалдық теңдеу
ші
ретті дифференциалдық теңдеу


 теңдеуінің
ретін төмендету әдісі
теңдеуінің
ретін төмендету әдісі -
рет интегралданған соң жалпы шешімін
аламыз
-
рет интегралданған соң жалпы шешімін
аламыз
 теңдеуінің
ретін төмендету әдісі
теңдеуінің
ретін төмендету әдісі

 ,
,
 ,
,


 ,
і=1,2,3,...,n
,
і=1,2,3,...,n