1.4. Виды зависимостей

В экономических исследованиях одной из основных задач является анализ зависимости между переменными. Зависимость может быть функциональной, статистической, корреляционной.

Функциональная зависимость задается в виде точной формулы, в которой каждому значению одной переменной соответствует вполне определенное значение другой.

В экономике функциональная зависимость между переменными проявляется редко. В большинстве случаев имеют место зависимости, когда каждому значению одной переменной соответствует не какое-то определенное, а множество возможных значений другой переменной. Иными словами, каждому значению одной переменной соответствует определенное (условное) распределение другой переменной. Такие зависимости называют статистическими.

Если каждому значению одной переменной соответствует определенное конечное условное математическое ожидание другой, то такая статистическая зависимость называется корреляционной. Таким образом, корреляционной зависимостью между двумя переменными называется функциональная зависимость между значениями одной из них и условным математическим ожиданием другой.

Аналитическая формула корреляционной зависимости между переменными называется уравнением регрессии. Если эта формула линейна, то имеет место линейная регрессия. В противном случае – нелинейная.

При рассмотрении зависимости объясняемой переменной от одной объясняющей переменной говорят о парной регрессии. Зависимость от нескольких объясняющих переменных называют множественной регрессией.

1.5. Ковариация и корреляция

Введем понятия ковариации и корреляции, которые будут необходимы для изложения основ регрессионного анализа.

Теоретическая ковариация

Теоретической (генеральной) ковариацией случайных величин X и Y называют математическое ожидание произведения отклонений этих величин от их математических ожиданий, т.е.

. (1.1)

Свойства теоретической ковариации.

1. - альтернативное выражение для вычисления .

Следствие. Если случайные величины X и Y являются независимыми, то .

Вывод. Ковариация является мерой взаимосвязи между X и Y.

2. .

3. , где – теоретическая (генеральная) дисперсия случайной величины X

4. , где a = const.

5. , где a = const.

6. Если , то .

7. .

Замечание. Для независимых случайных величин X и Y , поэтому .

Упражнение 1.1. Доказать, что .

Доказательство. По определению (1.1) имеем:

, что и требовалось доказать. При доказательстве использованы свойства математического ожидания случайных величин.

Выборочная ковариация

На практике не удается получить все данные по генеральной совокупности, и, как правило, теоретическая ковариация случайных величин X и Y неизвестна, но ее можно оценить (приближенно определить). Для ее оценки используют выборочную ковариацию, которую вычисляют по выборке объема n и обозначают .

Выборочной ковариацией случайных величин X и Y называется средняя арифметическая произведения отклонений этих величин от их средних, т.е.

= = . (1.2)

Свойства выборочной ковариации.

1. = = ,

где , .

2. = .

3. = , где – выборочная дисперсия случайной величины X.

4. = 0, где a = const.

5. = a , где a = const.

6. = ± .

7. Выборочная ковариация является смещенной (заниженной) оценкой теоретической ковариации, причем:

= .

Из свойства 7 следует, что в среднем за длительный период мы будем получать значения выборочной ковариации меньшие, чем теоретическая ковариация .

Упражнение 1.2. Доказать, что = .

Доказательство. По определению (1.2) имеем:

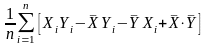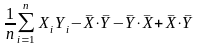= = = = = , что и требовалось доказать.

Выборочный коэффициент корреляции и проверка его значимости

По величине ковариации можно сделать вывод о зависимости или независимости случайных величин (для независимых случайных величин теоретическая ковариация равна нулю). Кроме того, по ковариации можно определить направление взаимосвязи. При наличии положительной ковариации переменные изменяются в одном направлении (связь прямая), если же ковариация отрицательна, то переменные изменяются в разных направлениях (связь обратная).

Однако существенным недостатком ковариации является ее зависимость от единиц измерения случайных величин X и Y. Поэтому тесноту взаимосвязи случайных величин X и Y с помощью ковариации определять неудобно. Для этого вводится относительная мера взаимосвязи (безразмерная величина) – коэффициент корреляции:

= . (1.3)

где – средние квадратические отклонения случайных величин X и Y.

Этот коэффициент корреляции называют теоретическим или генеральным.

С помощью коэффициента корреляции определяется теснота линейной связи между случайными величинами в генеральной совокупности.

Зависимость между случайными величинами X и Y, характеризуемая коэффициентом корреляции, называется корреляцией.

Если , то случайные величины X и Y являются некоррелированными, если же , то случайные величины X и Y коррелированны.

Как правило, генеральный коэффициент корреляции неизвестен. О тесноте линейной связи между переменными судят не по величине , а по величине его точечной оценки, вычисленной по выборке.

Оценкой теоретического (генерального) коэффициента корреляции является выборочный коэффициент корреляции:

, (1.4)

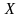где и – выборочные средние квадратические отклонения случайных величин и .

Замечание. В дальнейшем будем использовать следующие обозначения:

.

Так как вычисляется по значениям, случайно попавшим в выборку, то его величина меняется от выборки к выборке. В отличие от , выборочный коэффициент корреляции – величина случайная.

Пусть найденный по выборке коэффициент корреляции . Это еще не означает, что и . Чтобы установить, достаточна ли величина для обоснованного вывода о наличии линейной корреляционной связи между переменными X и Y, необходимо проверить значимость выборочного коэффициента корреляции .

Для этого выдвигаются нулевая (основная) и конкурирующая (альтернативная) гипотезы:

: r_ген = 0 (линейная корреляционная зависимость между переменными X и Y отсутствует, или статистически близок к нулю, т.е. статистически незначим),

: r_ген ¹№ 0 (переменные X и Y находятся в линейной корреляционной зависимости, или статистически далек от нуля, т.е. статистически значим).

По виду конкурирующей гипотезы определяют критическую область. В этом случае строят двустороннюю критическую область, описываемую неравенством: .

Нулевая гипотеза проверяется при заданном уровне значимости aa с помощью случайной величины

, (1.5)

которая при справедливости имеет распределение Стьюдента с числом степеней свободы , где объем выборки.

По выборочным данным вычисляют t_набл, а по таблице критических точек распределения Стьюдента находят t_{крит.дв}(aa, k) с учетом двусторонней критической области. Сравнивают t_набл и t_{крит.дв}(aa, k).

Если , т. е. наблюдаемое значение критерия попало в область принятия гипотезы, то нет оснований отвергать нулевую гипотезу. А если t_набл попало в критическую область, т.е. , то нулевую гипотезу отвергаем, принимаем конкурирующую Н₁.

Пример 1.1. Имеются выборочные данные о количестве внесенных удобрений ( , кг/га) и урожайности пшеницы ( , ц/га) по десяти фермерским хозяйствам:

	1	2	3	4	5	6	7	8	9	10
	19	16	19	14	23	22	27	33	28	29

1. найти выборочную ковариацию 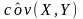, используя определение и альтернативную формулу для ее вычисления;

2. найти выборочный коэффициент корреляции ;

3. используя t-критерий, проверить значимость при 5%-ом уровне значимости.

Решение. Результативный признак – урожайность пшеницы, ц/га; факторный признак – количество внесенных удобрений, кг/га.

Замечание. Поскольку в условии приведены результаты конкретной выборки, то и представляют здесь реализации случайных величин и в i-ом наблюдении. Поэтому они обозначены малыми строчными буквами.

1. Вычислим по данной выборке , используя определение. Сначала найдем выборочные числовые характеристики признаков и .

Расчеты представим в таблице:

№ набл.
1 2 3 4 5 6 7 8 9 10	1 2 3 4 5 6 7 8 9 10	19 16 19 14 23 22 27 33 28 29	18 24,5 10 13,5 0 –0,5 6 25 17,5 27	19 32 57 56 115 132 189 264 252 290	1 4 9 16 25 36 49 64 81 100	361 256 361 196 529 484 729 1089 784 841
Итого	55	230	141	1406	7815	5630.

Выборочная средняя факторного признака ;

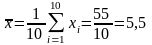Выборочная средняя результативного признака .

Таким образом, .

Теперь вычислим , используя альтернативное выражение, т.е. свойство 1:

= ,

где .

Заметим, что полученное разными способами значение совпадает.

2. Вычислим выборочный коэффициент корреляции по формуле (1.4):

r_в = .

Ранее получили, что = 14,1. Используя свойства 1 и 3 выборочной ковариации, найдем выборочные дисперсии факторного и результативного признаков:

, где ;

, где

Таким образом, .

3. Проверим значимость выборочного коэффициента корреляции. Для этого выдвигаем гипотезы:

.

По условию уровень значимости .

Для проверки нулевой гипотезы используем случайную величину , имеющую при справедливости распределение Стьюдента с числом степеней свободы . По выборочным данным найдем наблюдаемое значение критерия t_набл =    4,42. По таблице критических точек распределения Стьюдента определим t_{крит.дв}(0,05; 8) = 2,31. Сравниваем t_набл и t_крит(0,05; 8). Так как , т. е. t_набл попало в критическую область, нулевая гипотеза отвергается, принимается конкурирующая гипотеза: r_ген  0. Можно считать, что урожайность пшеницы и количество внесенных удобрений находятся в достаточно тесной корреляционной зависимости, r_в значим.