Мастер-класс профессора И.И. Боголепова: «Теория вероятностей и математичеая статистика в строительной акустике»

Мастер-класс профессора Боголепова Игоря Ильича: лекция «Теория вероятностей и математическая статистика

в строительной акустике».

Главная аудитория Инженерно-строительного факультета Санкт-Петербургского государственного политехнического университета.

11 мая 2011 года.

Введение

Завершение чего-то есть начало другого: сегодня на Инженерно-строительном факультете СПбГПУ коллоквиумом завершается строительная акустика (И.И. Боголепов. Строительная акустика. 2006), сегодня данной лекцией начинается теория вероятностей и математическая статистика в технике (И.И. Боголепов. Теория вероятностей и математическая статистика в технике. 2011). Новый курс лекций, прежде чем читать, его надо написать. Я прочитаю небольшой фрагмент из нового, только что написанного, курса лекций. Но, сначала вспомним: что это за наука «теория вероятностей и математическая статистика»? Дело в том, что наблюдаемые нами события можно подразделить на три вида: достоверные, невозможные и случайные. Достоверным называется событие, которое обязательно произойдет. Невозможным – событие, которое в данных условиях заведомо не произойдет. Случайным называют событие, которое может либо произойти, либо не произойти. Оказывается, что случайные события в массовых процессах подчиняются определенным закономерностям. Например, при большом числе бросания монеты в результате будет половина «орел» и половина «решка». Или − в этом помещении мы будем измерять в разных точках уровень звукового давления. В результате при большом количестве точек измерения получим зависимость величины уровня от числа измерений в виде кривой нормального распределения Гаусса. Науку «Теория вероятностей и математическая статистика» не надо путать с наукой «Статистика». Слово статистика происходит от латинского status - состояние дел. Статистика – древнейшая отрасль знаний – ей более трех тысячелетий. Она состоит их двух частей: 1. сбор и 2. анализ массовых совокупностей. Например, данные о численности населения в России (Федеральная служба государственной статистики Минэкономразвития РФ) или статистика промышленного производства в США (Федеральная резервная система США). Второй частью статистики − анализом массовых совокупностей – занимается молодая наука «Математическая статистика», которой не более трех столетий. Фундаментом её является «Теория вероятностей». Слово «вероятность» − математический термин, в обиходе давно звучит близкое по смыслу слово «шанс» − возможность осуществления чего-либо («Шансы на успех»), или «риск» − возможность удачи или неудачи («Риск – благородное дело»). Теория вероятностей и математическая статистика – громадный раздел современной математики. Суть небольшой части этого раздела − теории вероятностей и математической статистики в технике − состоит в следующем. Как бы ни были совершенны расчеты, измерения, испытания и технологические процессы, они не могут предусмотреть заранее влияния на них многочисленных случайных факторов. Эффект их воздействия приводит так или иначе к разным результатам, иногда весьма существенным. Необходимо уметь определять в цифрах точность и надежность результата инженерной деятельности, зависящего от случайных факторов. Без такого определения итоги могут оказаться ничтожными и даже опасными для людей, например, Чернобольская или Саяно-Шушенская катастрофы. Реальными событиями со случайными факторами занимается теория вероятностей.

В настоящее время нет практически ни одной области знаний, где бы ни применялись методы теории вероятностей и математической статистики. Данная лекция – пример применения этих методов в строительной акустике.

1. Статистическая оценка диффузности поля в строительной акустике

Строительная акустика занимается решением двух проблем: 1. Созданием прекрасных по восприятию звуков речи и музыка залов и 2. Уменьшением воздействия на человека шума в помещениях жилых, общественных и промышленных зданий. В решении этих проблем центральное место занимает статистическая оценка диффузности звукового поля в залах и помещениях, которая учитывает реальные факторы. С этой целью рационально использовать статистическую оценку звукового поля с помощью среднеквадратического отклонения генеральной совокупности уровней звукового давления , дБ, величины . Оценка эмпирического значения среднеквадратического отклонения определяется по формуле

= , (1.1)

где: n – число точек пространства зала или помещения, в которых производились измерения ;

– уровень звукового давления, измеренный в i-вой тчке пространства камеры;

= − среднее значение уровня звукового давления.

Если выборка производится из нормальной совокупности, то величина имеет - распределение с числом степеней свободы k и для вероятности P, которая подсчитывается так

= ( , имеем расчетную формулу

( (1.2)

Примем с вероятностью ( наибольшее из возможных значений за искомый стандарт генеральной совокупности (оценка сверху доверительного интервала) и получим в качестве критерия диффузности звукового поля при k ≤30 следующую величину:

(1.3)

Можно показать, что если k > 100, то с вероятностью близкой к единице наибольшее из возможных значений генерального стандарта примерно равно эмпирическому значению и получим критерий диффузности звукового поля для больших значений числа степеней свободы:

(1.4)

Статистическая оценка диффузности звукового поля при k > 100 необходима в первую очередь при аттестации звукомерных камер. Такие измерения, несмотря на их большой объем, надо обязательно выполнить. Их проводят один раз для данного устройства и данной методики измерения звукоизоляции и потом используют не только для оценки диффузности звукового поля камер, но, что очень важно, для оценки точности и надежности измерений звукоизоляции с наибольшей фактической точностью проведенных конкретных измерений звукоизоляции. Ниже представлены аттестационные частотные зависимости величины двух пар реверберационных камер для измерения звукоизоляции Центрального научно-исследовательского института технологии судостроения. На Рис. 1.1. представлены эмпирические значения , дБ, для больших звукомерных камер (БЗК), подсчитанные по формуле (1.1) по результатам измерений уровней звукового давления , дБ, в 162 точках камеры высокого уровня (КВУ) и 162 точках камеры низкого уровня (КНУ).

Рис. 1.1. Эмпирические значения , дБ, для БЗК:

1 – в КВУ; 2 – в КНУ

На Рис.1.2. показаны эмпирические значения для малых звукомерных камер для измерения звукоизоляции на малых моделях (МЗК), подсчитанные по формуле (1.1) по результатам измерений уровней звукового давления , дБ, в 144 точках камеры высокого уровня (КВУ) и 144 точках камеры низкого уровня (КНУ).

Рис. 1.2. Эмпирические значения , дБ, для МЗК:

1 – в КВУ; 2 – в КНУ

С какой частоты можно считать звуковое поле в камерах диффузным?

Многолетний практический опыт дает следующий результат.

Нижняя граничная частота , Гц, начиная с которой выше по частотному диапазону звуковое поле в реверберационной камере можно считать диффузным, в зависимости от объема камеры V, , приближенно оценивается по формуле известного немецкого акустика Эрвина Майера

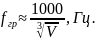(1.5)

По этой формуле в БЗК для камеры высокого уровня = 200 Гц и для камеры низкого уровня ≈ 250 Гц. По формуле (1.5) в МЗК для камеры высокого уровня ≈

630 Гц и для камеры низкого уровня ≈ 800 Гц.

Какие имеем результаты по статистическому анализу?

Поскольку в камерах высокого и низкого уровня БЗК и МЗК n > 100 , то генеральные значения стандарта определяется в зависимости от эмпирического значения стандарта по формуле

при надежности этой оценки

(t)

Если принять значение нормированной функции Лапласа (t) = 0,4973 и значит P = 0,9973 , то t = 2,79 и при n > 100 имеем .

Если принять по формуле Эрвина Майера для БЗК 250 Гц, то = 1,0 дБ. Аналогично для МЗК − 800 Гц и = 1,0 дБ. Здесь − наибольшее значение стандарта, при которым звуковое поле и в БЗК и в МЗК должно по статистическому анализу считать диффузным с надежностью P = 0,9973. Таким образом, статистическая оценка дает более точный результат и, главное, обеспечивает измерения звукоизоляции с высокой точностью и надежностью.