Эконометрика Временные ряды

Временной ряд – совокупность значений какого-либо показателя за несколько упорядоченных моментов.

Временной ряд представлен двумя основными категориями:

t – номер наблюдения;

y_t – уровень ряда, соответствующий моменту t.

Показатели анализы динамического временного ряда:

1. Абсолютный прирост:

а) цепной

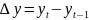
б) базисный

2. Темп роста:

а) цепной

б) базисный

3. Темп прироста:

а) цепной

б) базисный

Средние показатели:

1. Средний уровень ряда:

2. Средний абсолютный прирост:

3. Средний темп роста:

4. Средний темп прироста:

Вычисление показателей анализа динамики временного ряда в Excel (см. Файл Excel «Эконометрика_2new» Лист 1)

в табл. представлены данные о динамике инвестиций предприятия в основной капитал (тыс.долл.).

Инвестиции предприятия в основной капитал (тыс.Долл.)

Год Показатель	2001	2002	2003	2004	2005
Инвестиции в ок (тыс.долл.)	37,0	33,5	29,7	25,5	22,6

По данным табл. рассчитайте цепные, базисные и средние:

а) абсолютные приросты;

б) темпы роста;

в) темпы прироста.

В качестве базисного уровня возьмите начальный уровень ряда.

Дайте интерпретацию полученным средним характеристикам.

Сделайте прогноз на год вперед с помощью среднего абсолютного прироста и среднего темпа роста.

Выявление структуры ряда

Уравнение ряда формируется под воздействием трех составляющих:

1. Тренд (Т) – характеризует длительную тенденцию изменения процесса;

2. Сезонная компонента (сезонность S);

3. Случайная составляющая (ε).

Т.о. различают модели тренда,

сезонности,

а также тренд-сезонные модели

Последние можно разделить на 2 вида:

- аддитивные: T + S + ε

- мультипликативные: T · S · ε

Выявление структуры ряда

Определение структуры ряда означает выявление наличия в ряду тех или иных компонент, их видов и особенностей.

Т.е. нужно ответить на вопрос содержит ли ряд тенденцию. Если да, то сделать предположение о виде тренда. Затем определить наличие сезонной (циклической) компоненты, а также вид сезонной составляющей (аддитивная или мультипликативная). Также устанавливается период колебания.

Способы выявления структуры: графический метод и метод конечных разностей (используется для определения вида функции тренда).

Конечная разность первого порядка – это цепной абсолютный прирост: .

Конечная разность второго порядка – это разность между последовательными конечными разностями первого порядка:

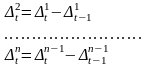
Заметим, что если конечные разности k-го порядка приблизительно равны, то конечные разности k+1 будут приблизит равны 0. Порядок конечных разностей k, остающихся примерно равными друг другу, принимают за степень выравнивающего многочлена.

Существует и третий метод – изучение автокорреляции функции ряда (АКФ). Как таковая автокорреляция это измерение зависимости между значением какой-либо величины из временного ряда и ее предыдущими или последующими значениями. АКФ – это зависимость коэффициентов автокорреляции уровней временного ряда от порядка.

Коэффициент автокорреляции уровней 1-го порядка – это коэффициент корреляции между исходным рядом и рядом сдвинутым на один период времени назад ( ).

Порядок коэффициента автокорреляции определяется лагом (т.е. периодом запаздывания).

Анализируя АКФ заметим: если наибольшим оказывается коэффициент автокорреляции 1-го порядка, то ряд содержит только тенденцию. Если наибольшим оказывается коэффициент автокорреляции k-го порядка, то ряд может содержать также сезонность с периодом k. Если ни один из коэффициентов не достаточно высок, то либо ряд не содержит не сезонности, ни тренда (только 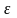), либо ряд содержит сильную нелинейную тенденцию.

Д ля определения формы модели сезонности изучают амплитуду колебаний относительно тренда. При аддитивной форме модели амплитуда постоянна (рис. слева), при мультипликативной – амплитуда со временем меняется (рис. справа).