2. Системи лінійних рівнянь

Система лінійних рівнянь з змінними має вигляд:

(1.2.1)

де , – довільні числа, які називаються відповідно коефіцієнтами при змінних і вільних членах рівнянь.

Розв’язком даної системи називається така сукупність чисел, при підстановці яких кожне рівняння системи перетворюється у вірну рівність.

Система рівнянь називається сумісною, якщо вона має хоча б один розв’язок , і несумісною, якщо вона не має розв’язків.

Сумісна система рівнянь називається визначеною, якщо вона має єдиний розв’язок , і невизначеною, якщо вона має більше одного розв’язку.

Наприклад, система рівнянь – сумісна і визначена, тому що має єдиний розв’язок ; система – несумісна; а система рівнянь – сумісна і невизначена, тому що має більше одного , а точніше множину розв’язків.

Дві системи називаються рівносильними, або еквівалентними, якщо вони мають одну і ту ж множину розв’язків. За допомогою елементарних перетворень системи рівнянь (розглянутих стосовно до матриць) отримують систему, рівносильну даній.

Запишемо дану систему в матричній формі. Позначимо:

; ; ,

(1.2.2)

де – матриця коефіцієнтів при змінних, або матриця системи, – матриця-стовпець змінних, – матриця-стовпець вільних членів.

Тому що число стовпців матриці дорівнює числу рядків матриці , то їхній добуток

є матриця-стовпець. Елементами отриманої матриці є ліві частини даної системи. На підставі визначення рівності матриць систему можна записати у вигляді:

.

(1.2.3)

Нехай число рівнянь системи дорівнює числу змінних, тобто . Тоді матриця системи є квадратною, а її визначник називається визначником системи.

Методи розв’язання систем лінійних рівнянь:

1. Метод оберненої матриці. Для одержання розв’язку системи при в загальному виді припустимо, що квадратна матриця системи невироджена, тобто її визначник . У цьому випадку існує обернена матриця . Множачи ліворуч обидві частини рівності на матрицю , одержимо. Тому що , то розв’язком системи в матричній формі буде матриця-стовпець

   .

   (1.2.4)

2. Інший метод розв’язання системи рівнянь ґрунтується на теоремі Крамера. Складемо визначник матриці системи :

Випишемо допоміжні визначники , що відповідають кожній змінній

, які отримують шляхом заміни -го стовпця основного визначника стовпцем вільних членів :

, ,…, ...

_Тоді:

• якщо , то система має єдиний розв’язок , який обчислюється за формулами Крамера:

  , , … , ;

  (1.2.5)

• якщо , а серед визначників є не рівні нулю, то система несумісна;

• якщо і всі , то система має нескінченну множину розв’язків.

Приклад 1.2.1. Розв’язати систему рівнянь

Розв’язання. а) Розв’яжемо систему методом Крамера. Випишемо матриці і :

, .

, ,

, .

Розв’язок системи такий:

, , .

Перевірка показує, що , , задовольняють рівнянням даної системи, отже, є її розв’язком.

б) розв’яжемо систему методом зворотної матриці. Випишемо матриці , і :

, , .

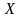Знайдемо , для цього випишемо алгебраїчні доповнення матриці :

;	;	;
;	;	;
;	;	.

Тоді .

Розв’язок системи знайдемо з рівності :

.

Отже,

, , .

Метод оберненої матриці і метод Крамера є дуже трудомісткими за кількістю обчислювальної роботи. Тим часом існують більше економічні методи розв’язання систем лінійних рівнянь, які опираються на попереднє перетворення матриці системи до спеціального виду. Одним з них є метод Гаусса, що застосовується не тільки у випадку, коли .

Метод Гаусса – метод послідовного виключення змінних – полягає в тому, що за допомогою елементарних перетворень система рівнянь приводиться до рівносильної системи східчастого (або трикутного) виду, з якої послідовно, починаючи з останніх (за номером) змінних, знаходять всі інші змінні. Розглянемо застосування цього методу на конкретному прикладі.

Приклад 1.2.2. Розв’язати систему рівнянь

Розв’язання. Перший етап. Перше рівняння системи залишимо без змін, а із другого і третього рівнянь виключимо :

Другий етап. Перше і друге рівняння системи залишаємо без змін. Із третього рівняння виключаємо змінну :

Третій етап. Підставимо в друге рівняння системи і знайдемо ; при підстановці в перше рівняння системи, одержуємо . Розв’язок системи може бути записане у вигляді:

.

Перетворення Гаусса зручно проводити, здійснюючи перетворення не із самими рівняннями, а з матрицею коефіцієнтів. Розглянемо матрицю

,

яка називається розширеною матрицею даної системи; у неї, крім матриці системи , додатково включено стовпець вільних членів.

Приклад 1.2.3. Розв’язати систему рівнянь

Розв’язання. Розширена матриця системи має вигляд:

.

Перший рядок матриці помножимо послідовно на (–2), (–3), (–2) і, додамо відповідно до другого, третього, четвертого рядків, виключимо змінну із всіх рядків, починаючи з другого:

.

Повернемося від отриманої розширеної (трикутної) матриці до системи рівнянь і знайдемо розв’язок системи:

Приклад 1.2.4. Методом Гаусса розв’язати систему рівнянь:

Розв’язання. Перетворимо розширену матрицю системи:

.

Отже, рівняння, що відповідає третьому рядку останньої матриці, суперечливо – воно звелося до невірної рівності , тобто, дана система несумісна.