4.2. Понятие функции. Основные свойства функций.

Постоянной величиной называется величина, сохраняющая одно и то же значение. Например, отношение длины окружности к ее диаметру – число π.

Переменной называется величина, которая может принимать различные числовые значения. Например, при равномерном движении , где путь S и время t – переменные, или площадь треугольника , где S – площадь, h – высота, a – постоянное основание.

Перейдем к понятию функции.

Определение. Если каждому значению x множества Х ставится в соответствие вполне определенное значение у множества Y , то говорят, что на множестве Х задана функция .

При этом х называется независимой переменной, или аргументом, у – зависимой переменной, а буква f обозначает закон соответствия.

Множество Х называется областью определения, или существования, функции, а множество Y – областью значений функции.

Под символом понимается значение функции при . Можно записать в виде . Если области определения, то символ не имеет смысла.

Примеры. Найти область определения функций:

1. , область определения Х:

2. , область определения Х:

3. , область определения – множество чисел, удовлетворяющих условию , или . На числовой оси это есть точки (числа), удовлетворяющие условию и .

Способы задания функции.

Существует несколько способов задания функции.

а) Аналитический способ, если функция задана формулой вида . Этот способ наиболее часто встречается на практике. Так, функция задана аналитически.

Не следует смешивать функцию с ее аналитическим выражением. Например, одна функция

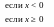
имеет два аналитических выражения: (при ) и (при ).

б) Табличный способ, если функция задана таблицей, содержащей значения аргумента х и соответствующие значения функции , например таблица логарифмов.

в) Графический способ, если функция изображена в виде графика – множества точек (х,у) плоскости, абсциссы которых есть значения аргумента х, а ординаты которых – соответствующие им значения функции у f(x).

г) Словесный способ, если функция описана правилом ее составления, например, функция Дирихле: , если х – рационально, , если – х иррационально.

д) Функция может быть задана программой, вычисляющей ее значения с помощью компьютера.

Основные свойства функций. К ним относятся четность и нечетность, монотонность, ограниченность, периодичность.

1. Четность и нечетность. Функция называется четной, если для любых значений х из области определения , и нечетной, если . В противном случае функция называется функцией общего вида.

Например, функция является четной, так как и , а функция - нечетной, так как и . В то же время, например, функция является функцией общего вида, так как и , .

График четной функции симметричен относительно оси ординат (см., например, график функции на рис. 4.12), а график нечетной функции симметричен относительно начала координат (см., например, график функции на рис. 4.13).

2 . Монотонность. Функция называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.

Пусть и . Тогда функция возрастает на промежутке Х, если , и убывает, если (рис. 4.8).

Функции, возрастающие и убывающие, называются монотонными функциями. Так, например функция (см. рис. 4.12) при убывает и при возрастает.

3. Ограниченность. Функция называется ограниченной на промежутке Х, если существует такое положительное число M>0, что для любого . В противном случае функция называется неограниченной. Например, функция ограничена на всей числовой оси, ибо для любого x R. (рис. 4.9).

4. Периодичность. Функция называется периодической с периодом , если для любых х из области определения функций . Например, функция имеет период , так как для любых значений х .

График периодической функции может быть получен сдвигом кривой ( ) вправо (влево) на отрезки Т, 2Т, … (рис. 4.10).

Обратная функция. Пусть есть функция от независимой переменной х, определенной на множестве Х с областью значений Y. Поставим в соответствие каждому единственное значение , при котором . Тогда полученная функция , определенная на множестве Y с областью значений Х, называется обратной.

Так как традиционно независимую переменную обозначают через х, а функцию – через у, то функция, обратная к функции , примет вид . Обратную функцию обозначают также в виде (аналогично с обозначением обратной величины). Например, для функции y a^x обратной будет функция x log_ay, или (в обычных обозначениях зависимой и независимой переменных) .

Можно доказать, что для любой строго монотонной функции существует обратная функция.

Г рафики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов (на рис. 4.11 показаны графики взаимно обратных функций и при ).

Сложная функция. Пусть функция есть функция от переменной u, определенной на множестве U с областью значений Y, а переменная u в свою очередь? является функцией от переменной х, определенной на множестве Х с областью значений U. Тогда заданная на множестве Х функция называется сложной функцией (функцией от функции). Например, - сложная функция, так как ее можно представить в виде , где .