2. Асинхронды машинаның кернеулер және тоқтар теңдеулері, алмастыру схемасы және асинхронды машинаның векторлық диаграммасы

Асинхронды қозғалтқыш статоры орамасының электр тепе-теңдігінің теңдеуі. Асинхронды қозғалтқыш статорының орамасына берілген желі кернеуі U₁ шашыранды индуктивтік І,ј Χ₁ және ораманың активті кедергісі і, r кернеулерден пайда болған негізгімагнит ағыны Е₁ мен шашыранды ағын Е _1δ ЭҚК арқылы тепе-теңдікке келеді, демек:

U₁ = E₁ + І₁ r₁ + І₁ ј х₁ (2.29 )

мұндағы r₁- статор орамасының активті кедергісі:

r= R + R_1ст (2.30 )

мұнда R₁ – статор орамасы өткізгіштің Омдық кедергісі; R_1ст –болаттың электр кедергісі, ол магниттік және статор теміріндегі гистерезис құбылысы мен құйынды тоқтардан болатын электр шығындарына пропорционал. Е₁ ЭҚК-нің әрекеттік мәні "-" таңбасы болады. Ленц заңы бойынша ол тоқ көзіне U₁ қосылған тұтынушы ретінде статор орамасында индукцияланады. (2.29) теңдеуі трансформатордың бірінші орамасының электрлік тепе-теңдігімен бірдей (1.20).

Асинхронды қозғалтқыш ротор орамасының электрлік тепе-теңдік теңдеуі. Асинхронды қозғалтқыштардың роторы орамасының электрлік тепе-теңдігі жұмыс жасаған кезде трансформатордың екінші орамасы, егер ол қысқартылған және айналатын болса (U₂=0) теңдеуімен бірдей:

0 = Е_2S – І₂ r₂ –І₂ јх_2S (2.31 )

(2.31) теңдеуінде U₂= 0, себебі ротор орамасы ажыраулы кезінде асинхронды қозғалтқыш айнала алмайды, (2.31) теңдеуі тәжірибеде қолдануға ыңғайсыз, себебі ротор орамасы ажыратулы кезінде асинхронды қозғалтқыш айнала алмайды. (2.31) теңдеуді тәжірибеде қолдануға ыңғайсыз, себебі ондағы ЭҚК Е_2S пен шашыранды индуктивті кедергі х_2S, асинхронды қозғалтқыштың білігіне түсетін жүктеменің өзгертуімен бірге өзгеріп отырады. (2.31) теңдеуіндегі Е_2S ті sЕ₂ (2.15) және х_2S,ті sŁх₂ (2.22) мен алмастырып мынадай түрге келтіреміз:

О =sE₂ – І₂ r₂ – І₂sјх₂ (2.32 )

(2.32) теңдеуінің екі бөлігінде сырғанауға s бөлсек, бір айнымалы s сырғанауы бар теңдеуін аламыз:

(2.33 )

мұндағы Е₂ мен х₂ –тоқтатылған ротор орамасының ƒ₂=ƒ₁ кезіндегі ЭҚК мен шашыранды индуктивтік кедергісі. Олардың мәндері тұрақты болады. Ротордың тоғы s сырғанауға байланысы ғана өзгеретін болады:

(2.34 )

Нақты және келтірілген трансформаторға тежелген асинхронды қозғалтқыш статоры мен роторы орамаларының электрлік тепе-теңдігі теңдеулерінің жүйелері. (2.33) теңдеу тежелген актив кедергісі 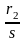және шашыранды индуктивті кедергісі х₂ ротор орамасы бар трансформаторша жұмыс істейтін, асинхронды қозғалтқыштың теңдеуі. Сонымен, шынайы асинхронды қозғалтқыш статоры мен роторы орамаларының электрлік тепе-теңдігі теңдеулер жүйесін құрады:

, (2.35 )

ал трансформаторша істейтін тежелген асинхронды қозғалтқыш үшін:

(2.36 )

Асинхронды қозғалтқыштың алмастыру эквивалентті электр сұлбалары. Асинхронды қозғалтқыштың орнын басатын электрлік тепе-теңдік теңдеуінің теориялық сипаты ғана бар және оның тікелей жұмыс тәртібіне талдау жасауға және жұмыс сипаттамаларын есептеуге пайдалануға қолданыла алмайды:

- бірінші теңдеуден тоқтың мәнін анықтау мүмкін еместігі себебі Е₁-дің сан мәні жоқ және векторлар Ů₁ мен І₁ дің арасындағы ығысу бұрышы көрсетілмеген;

• статор мен ротор орамаларындағы тоқтардың арасындағы байланыс жоқ, ол асинхронды қозғалтқыштағы электромагниттің физикалық болмысына қарсы келеді.

Бұл мәселе нақты асинхронды электроқозғалтқыштың магнит өткізгіші бар және статор мен ротор орамаларының өзара индуктивтігі мен болат магнит өткізгіші бар өзара индукцияланбайтын сызықтық эквивалентті электр тізбегі бар құрылғы электротехникалық тізбекпен алмастыру арқылы шешіледі. Ол үшін айналатын асинхронды қозғалтқыш әуелі қозғалмайтын (тежелген) трансформаторша істейтін активті тең кедергісі бар екінші (ротордың) орамалы және шашыраңқы индуктивті кедергімен х₂ алмастырылады. Ал одан соң, , трансформаторларға қолданылған әдістеме бойынша, екінші ораманың (ротор орамасы) өлшемдері бірінші орамаға (статор орамасына) келтіріледі.

Мұнда электрлік тепе-теңдіктің (2.33) теңдеуіндегі асинхронды қозғалтқыш орамасының активті кедергісі r₁ мен роторы орамасының r₂ Омдық кедергімен алмастырылады (R₁ және R₂) оған магниттендіру тізбегі болатының кедергісі R_сm қосылады, ол активті және реактивті құрамынан тұрады:

, (2.37)

мұндағы І^'_μа гистерезис құбылысы мен құйынды тоқтардан болатын шығынды жабуға кеткен магниттендіргіш тоқтың активті құраушысы; І_Ұр^' - асинхронды қозғалтқыштың магнит ағыны Ф туғызатын магниттендіргіш тоғының реактивті құраушысы. Осындай ауытқулардан магниттендіргіш тоқтың І_Ұ^' магнит ағынымен уақыт жағынан үйлеспеуі магнит өткізгіш болатындағы магниттік шығын бұрышындай болады. Оның сан мәні былай анықталады:

, (2.38)

мұндағы

; (2.39)

(2.40)

сонымен, егер нақты асинхронды қозғалтқышта ЭҚК Е₁ ті өзара индукцияланудың кедергісіне түскен кернеумен теңестіруге болатын болса (Е₁=I_μjX_μ), ал трансформаторға келтірілген тежелген (тоқтатылған) қозғалтқышта ЕҚК болаттағы электр шығынына пропорционал болатын болат кедергісіне түскен кернеудің І_µ^'R_ıcт шамасына қарай өзгереді. Дегенмен, нақты асинхронды қозғалтқыштың келтірілгенге өту кезіндегі өлшемдерін өзінше түсіндіру бірін-бірі сандық жағынан айтарлықтай өзгеріс туғызбайды. Осыдан шығатын, асинхронды қозғалтқыш роторы орамасының өлшемдерін қозғалтқыш статоры орамаларының өлшеміне эквивалентті өзгерту, нақты қозғалтқыш роторы орамасының электрлік тепе-теңдік теңдеуіндегі қатынасын сақтау шарты бойынша іске асырылады (2.33). Егер теңдеудің (2.33) екі жағынан коэффициент іне көбейтсек, оң жағының соңғы қосылғышын тағы көбейтсек, ал онда мынадай түрге келеді:

0 = - (2.41)

егер: ; (2.42)

; (2.43)

; (2.44)

, (2.45)

белгілесек, онда тежелген асинхронды қозғалтқыш роторы орамасының статор орамасына келтірілгендегі электрлік тепе-теңдік теңдеуіе аламыз:

, (2.46 )

мұндағы Ė₂^/, І₂^/; R₂^/; х₂^/- сәйкес, трансформаторша жұмыс істейтін тежелген асинхронды қозғалтқыштың статор орамасына келтірілген ротор орамасының ЕҚК, тоғы, омдық және шашыраңқы индуктивтік кедергісі (2.31), (2.43) және (2.42) теңдеуіндегідей көрсетілгендей қозғалтқыштарға Е₂=Е₁ тән, бұл табиғи нәрсе, себебі ротор орамасының келтіру барысының нәтижесінде статор орамасымен w₁=w₂ және К₀₁=К₀₂ болып бірігісіп кетті. (2.25) пен (2.36) теңдеулерін ескере отырып, ротор орамасына келтірілген тежелген асинхронды қозғалтқыштардың электрлік тепе-теңдік теңдеулері жүйесін құрады.

(2.47)

(2.47) теңдеулер жүйесіне сүйене отырып, магнит байланысы бар нақты асинхронды қозғалтқыш магнит байланысы жоқ сызықтық орын басушы эквивалентті электр сұлбасымен ауыстырылады. Мұнда ротор орамасында индукцияланатын ЭҚК Е_2S=SЕ₂ және индуктивті шашырандылық кедергісі х_2S=Sх₂ сияқты сырғанауға тәуелді өлшемдер, олардың қозғалмайтындай тұрақты мәндерімен R₂ сыранауға тәуелді 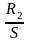саналатын, ауыстырылады. Мұндайда тұтынылған қуат электр шығындары және электрлік процесстерді нақты қозғалтқышпен орнын басатын эквивалентті электр сұлбасында жағдайлар жағынан бірдей болады, бұл айналып тұрған қозғалтқыштың жұмыс тәртібін қозғалмай тұрған қозғалтқыш арқылы талдауға мүмкіндік береді. Асинхронды қозғалтқыштың орнын басатын эквивалентті электр сұлбасы электрлік тепе- теңдіктің толық теңдеулері жүйесі негізінде құрылады (2.47) ондағы электрлік кедергілері мен оларды жалғау сұлбалары, ол үшін Кирхгордың бірінші және екінші заңдары бойынша құрылған теңдеулер, электрлік тепе-теңдік теңдеуімен (2.47) дәл келуі тиіс.

Ол келтірілген трансформатордың келтірілген сұлбасымен бірдей. 2.15-суретте көрсетілген асинхронды қозғалтқышты ауыстыратын Т-тәрізді сұлба делінеді, онда:

Z₁ =R₁ +j х₁-статор орамасының омдық R₁ және шашыранды индкутивті кедергісінен х₁ тұратын толық электр кедергісі;

ротор орамасының омдық кедергінің келтірілген мәні R₂¹ мен тежелген ротордың шашыранды индукциялық кедергісі:

келтірілген асихронды қозғалтқыштың болат кедергісі R_ст мен өзара индукцияланудың индуктивті кедергісінен х_м тұратын магниттену тізбегінің толық электр кедергісі.

Асинхронды қозғалтқыштың жұмысын зерттеу үшін Т тәрізді орынбасар сұлбасы ыңғайсыз, себебі сырғанаудың өзгертуінен барлық үш тармақағы тоқ, тіпті U₁=соnst болғанның өзінде, өзгереді. Аса күрделі емес бірнеше түрлендірулер жасау арқылы асинхронды қозғалтқыштың орынабасу Т–тәрізді сұлбасынан Г-тәрізді эквивалентті сұлбасына өтуге болады.

Егер ауысу (түрлендіру) процесін былай деп қарасақ:

; (2.48)

; (2.49)

; (2.50)

, (2.51)

онда Г-тәрізді орынбасу сұлбасы 2.16-суреттегідей түрге келеді.

2.15-сурет. Асинхронды қозғалтқыштың алмастырма эквивалентті Т-бейнелес электр сұлбасы.

2.16-сурет. Асинхронды қозғалтқыштың орнын басудың Г-бейнелес эквиввалентті анық электр сұлбасы.

Түзе коэффициенті кешенде реактивті құраушының аздығынан оның заттық бөлімі ғана есепке алынады:

(2.52)

оның сандық мәні С 1,05…1,02 аралығында алынады. Есептегенде, инженерлік тәжрибеге қолайлы болу үшін С-тың мәнін 1,0 деп алады, бұл Т және Г тәрізді сұлбалардың екінші тармағындағы тоқтар кешендерінің теңесуіне әкеледі (İ₂^ң= İ₂¹). Бұл жағдайда х₁ кедергісін ( ), елемеуге тура келеді бұл қуаттылығы кіші асинхронды қозғалтқыштарға тиімсіз, себебі олар үшін (х₁>0).

Орынының басудың Г тәрізді сұлбасында Т тәрізді сұлбада байқалған кемшіліктер жоқ. Соның көмегімен сызықтық электр тізбегінің теориясының белгілі өрнекті пайдаланып, асинхронды қозғалтқыштың әртүрлі жұмыс тәртібіндегі жұмыс сипаттамаларын есептеу жеңіл. İ₀ синхрондылық тоғы болып табылады, оның сандық мәні асинхронды қозғалтқыш роторының синхронды айналу жылдамдық (n₂=n₁) кезінде тұтынылған тоғына тең, мұнда статор орамасы мен оның болаттарындағы тоқ шығындары ескеріледі. Мұндай режимді орнату, асинхронды қозғалтқыш білігін механикалық энергияның басқа көзіне, мысалы онымен полюстері тең синхронды қозғалтқышқа қосу арқылы айналдырғанда ғана мүмкін. Бұл кезде İ₀

, (2.53)

ол асинхронды қозғалтқыштың жұмыс режиміне (біліктегі кедергі моментіне) тәуелді болмайды, İ₀ мен İ₂^ң тоқтары өзгерген кезде де өзгеріссіз қалады.

2.17-сурет. Асинхронды қозғалтқыштың орнын ауыстырудың Г-бейнелес эквивалентті анықталған электр сұлбасы.

Егер 2.16-суретте көрсетілген сұлбадағы Ĉ кешенін оның модуліне С₁, ал С₁Z₁ =Z¹ мен C²₁ ŁZ_2S¹ = Z^"_2Sке алмастырса онда 2.17-суретте көрсетілген сияқты орнын ауыстырудың дәлденген сұлбасына өтуге (ауысуға) болады:

онда

(2.54)

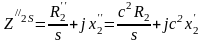(2.55)

емес.

3. Асинхронды қозғалтқыштардың арналымы. Асинхронды қозғалтқыштар құрлысының қарапайымдылығы мен жұмысының сенімділігі арқасында адамзат тіршілігінде, иінді біліктерді айналдыруға механикалық энергияны керекететін қызметтердің бәрінде кеңінен пайдаланылып келеді.

Ауылшаруашылығында шаңды орта мен химиялық зиянды орталарда жұмыс жасай алатын бірден-бір электр қозғалтқыш осы асинхронды мәшине ғана. Асинхронды қозғалтқыштарды, үшфазалы және бір фазалы электр желілеріне қосу үшін үшфазалы немесе бір фазалы етіп жасайды. Үшфазалы асинхронды қозғалтқыштар роторларының орамаларының түрлеріне қарай, фазалық немесе қысқа тұйықталған роторлары асинхронды қозғалтқыштар деп бөледі. Ауылшаруашылығында, негізінде механикалық энергияның ең арзан әрі сенімді көзі ретінде қысқа тұйықталған роторлы асинхронды электроқозғалтқыштар қолданылады.

9 дәріс

Модуль 2.Асинхронды машиналар

Тақырып 3. Асинхронды машинаның айналу моменті және оның сырғанауға, кернеу параметрлеріне тәуелділігі.

3.1.Асинхронды қозғалтқыштың энергетикалық диаграммасы.

3.2. Асинхронды қозғалтқыштың айналдыру моменті.

3.3. Асинхронды қозғалтқыштың жұмысшы сипаттамасы.

3.1.Асинхронды қозғалтқыштың энергетикалық диаграммасы. Асинхронды қозғалтқыш статоры орамасына берілген электр энергиясының білікті айналдыратын механикалық энергияға айналуы, оның машиненің әртүрлі бөлшектерінде шығын болуымен байланысты. Бұл асинхронды қозғалтқыштың жұмыс қасиеттерін білуде зор маңызы бар процесс.

2.18-суретте асинхронды қозғалтқыштың статоры орамасына берілген электр энергиясының білікті айналдыратын механикалық энергияға айналу сатылары бойынша анық қадағалауға, ондағы электр шығындарын білуге мүмкіндік береді.

Үш фазалы асинхронды қозғалтқыштың электр желісінен алған активті қуаттылығы ЭТН курсынан белгілі өрнек бойынша анықталады:

(2.56)

Бұл қуаттың бір бөлігі статор орамасының өткізгіштері арқылы өткенде жұмсалады. Қуаттың бұл шығындары мыстағы электр шығындары деп аталады:

, (2.57)

мұндағы R₁ статор орамасы фазасындағы Ом кедергілері; І₁–статор орамасыфазасындағы тоқ.

Электр қуатының мыстағы шығыны жылуға айналады да, статор орамасын қыздырады. Желіден тұтынылған қуаттың енді бір бөлігі асинхронды қозғалтқыш статорының болаттарында пайда болған айнымалы магнит өрісінің әсерінен болатын құйынды тоқтар мен гистерезис құбылысына шығындалады. Олар статор болатындағы электр шығындары делініп мына өрнекпен анықталады:

(2.58 )

Құйынды тоқ Р_құй мен гистерезис Р_гс шығындары статор теміріндегі магнит индукциясының В_с жиілігінің өзгеруіне тәуелді. Олардың қорытынды мәні мына өрнекпен есептеледі:

, (2.59)

мұндағы Р₍₅₀₎ =(1,7…4,0); В=1,0 Тл және ƒ=50Гц кезінде статор болатының сортына және қаңылтырдың қалыңдығына байланысты болатын меншікті шығын; В_с –статор болатындағы есепті индукция, Тл; G - статор массасы, кг.

2.18-сурет. Асинхронды қозғалтқыштың энергетикалық диаграммасы.

2.19-сурет. Қысқа тұйықталған роторлы асинхронды қозғалтқыштың механикалық шығындары (Рмех).

Статор болатындағы шығын статорды қыздыратын жылу ретінде де көрінеді. Мыстағы шығындар Р_м мен статор орамасындағы және ротор болатындағы шығындарды алып тастаған соң қалған қуат электр магниттік қуат делінеді.

(2.60)

Ол магнит өрісі арқылы ауа саңылауы бойынша асинхронды қозғалтқыштың раторына шығынсыз беріледі, ротордың орамасы тұйықталғанда онда және статорда қуаттың бір бөлігі орама өткізгіштерінде Р_м(а)2 және ротор болатындағы Р_с2 құйынды тоқтар мен гистерезистен электр шығындары ретінде жұмысалады.

Ротор орамасы мысындағы (алюминийде) шығындар сандық тұрғыдан мына өрнекпен анықталады:

, (2.61 )

мұндағы m₂–ротор орамасының фазалар саны; І₂ – ротор орамасы фазасының тоғы; R₂–ротор орамасы фазасының өткізгіштерінің кедергісі. Жұмысшы сырғанау шегі S<0,1 болғандықтан ротор болатындағы шығындарды, әдетте елемейді (Р_с2 О). Қажет кезінде оны Р_с2=Р_(1/50) S^β В_р² G_р өрнегі бойынша есептейді, мұндағы В_р – ротордағы индукция; G_р –ротор болатының массасы; S-сырғанау; β=(1,2…1,5)- ротор болатының сортына байланысты дәреже көрсеткіші. Ротор мысындағы (алюминииде) шығынды Р_м(А)2 алып тастағаннан кейінгі қуат, асинхронды қозғалтқыштың роторы дамытатын механикалық қуат Р_мех деп аталады. Сонымен асинхронды қозғалтқыш роторы дамытатын механикалық қуат, оған статор орамасының магнит өрісі берген электр магниттік қуаттан, ротор орамасындағы электр шығындарындай шамаға аз болады.

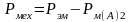(2.62)

Асинхронды қозғалтқыштардың біліктеріндегі механикалық қуат қозғалтқыш роторындағы механикалық қуаттан қосымша шығындар Р_қос шамасындай аз болады. Қосымша шығындарға қозғалтқыштың айналатын бөліктерінің ауамен үйкелісіне, айгөлектердің үйкелісіне, шашыраңқылық ағынына, статор мен ротордың тістеріне магнит ағындарының жоғары горманикасына және басқа да себептерден болатын үстеме шығындар Р_ү жатады.

Қосымша шығындарды есептеу деңгейінің дәлдігі іс жүзінде аса жоғары емес. Сондықтан олар қозғалтқыштың желіден алған активті қуатының пайыздық қатынас шамасында мөлшерлеп алынады. Қалыпты жүктемеде қосымша шығындар қозғалтқыш тұтынған қуаттың (1,8…0,8)% ін құрайды:

(2.63)

Қосымша шығындарды толығырақ есептеу үшін олардың құраушыларын жеке-жеке, ол үшін Р_ү =0,005Р деп алып, Р_мех-ті 2.19–суретте көрсетілген қисық сызықтар бойынша анықтайды. Сонымен, қозғалтқыш бетіндегі механикалық қуат Р₂ қозғалтқыштың желіден тұтынған қуатынан Р₁ жоғарыда аталған барлық шығындарды алып тастағандағы айырмасына тең.

, (2.64)

мұнда ∆ P = P_м1+Р_с1+Р_м2 +Р_ү

Тиімді пайдаланған қуаттың (біліктегі қуат) асинхронды қозғалтқыштың электр желісінен тұтынған активті қуатына қатынасы оның ПӘК-ін анықтайтындықтан:

(2.65)

Бұдан асинхронды қозғалтқыш білігіндегі механикалық қуат электр өлшемдері арқылы мына теңдеумен өрнектеледі:

(2.66 )

2.20-сурет. Асинхронды қозғалтқыштың механикалық сипаттамасы М=f(S).

2.21-сурет. Қысқа тұйықталған роторлы асинхронды қозғалтқыштың жылдамдық (механикалық) сипаттамасы n =f (M).

3.2. Асинхронды қозғалтқыштың айналдыру моменті. Асинхронды қозғалтқыш білегіндегі айналдыру моменті механикаден белгілі, мына өрнек арқылы Ньютонмен анықталады.

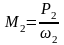, (2.67)

мұндағы ротордың бұрыштық айналу жиілігі, рад/с; Р₂- біліктегі қуат, Ватт.

(2.67) дағы ω₂ ні (2.14) арқылы алмастырып, асинхронды қозғалтқыш білігіндегі моментті сырғанау функциясы түрінде аламыз:

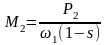, (2.68)

мұндағы ω₁–статор орамасының магнит өрісінің синхронды бұрыштық айналу жиілігі.

(2.21)–теңдеу асинхронды қозғалтқыш білігіндегі моменттің өзгеру сипаты туралы толық мағлұмат бермейді, себебі сырғанаудың өзгеруімен бір уақытта оның қуаты да өзгереді. Онымен қоса, жүргізіп жіберу кезінде, S=1,0 кезінде (2.21) теңдеуі анықталмаушылыққа келтіреді: .

Асинхронды қозғалтқыштың жұмыс қасиеттерін зерттеу үшін момент теңдеуін бір айнымалысы бар функцияға, мысалы жылдамдыққа немесе сырғанауға келтіру керек. Электрмагниттік моментті электрмагниттік қуат пен қозғалтқыш статоры орамасының магнит өрісінің бұрыштық айналу жиілігі арқылы көрсетіп мынаны аламыз:

, (2.69)

мұндағы

(2.70)

Асинхронды қозғалтқыш (2.17-сурет) роторы орамасының Омдық кедергісі R₂ мен тоғы І₂ эквивалентті электр сұлбасы өлшемдері арқылы…

; (2.71)

, (2.72)

болғандықтан, онда

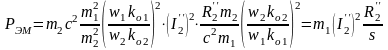(2.73)

І₂^" тоғын Ом заңы бойынша жазып Г тәрізді орнын басу сұлбасы (2.17-сурет):

, (2.74)

оны (2.73)-теңдеуге қою арқылы, асинхронды қозғалтқышты эквивалентті электр сұлбасы арқылы электрмагниттік қуаттың туаттың түбегейлі өрнегін аламыз:

(2.75)

Сонда асинхронды қозғалтқыштың іздеген электр магниттік теңдеуі 2.69 сырғанау S функциясында қалған басқа өлшемдері тұрақты болғанда, былай жазылады:

(2.76)

Іс жүзінде асинхронды қозғалтқыш білігіндегі моменттің М₂ электрмоментінен М_эм айырмасы аз, себебі:

М₂ = М_эм – М_о (2.77)

мұндағы М₀–бос жүріс кедергісінің моменті, олар айгөйлектегі механикалық үйкелістен, сондай-ақ статор мен ротор тістеріндей магнит өрістерінің соғуынан құралады. Көп жағдайда оларды М₂ М_мэ = М деп санап (2.78) ескермеуге болады. 2.20-суретте (2.76) теңдеуі бойынша тұрғызылған М=ƒ(S) қисығы көрсетілген. Одан асинхронды қозғалтқыш моментінің сырғанауға байланысты. Өзгеру сипаты күрделі екенін көреміз. Сырғанаудың көбейуіне қарай жүктеменің артуына сәйкес. Біліктегі момент шырқау шегі мәніне дейін артады. М_мах да 2.20-суреттегі 2 нүктесіне дәл келеді. Сырғудың (жүктеменің) одан ары ұлғаюында момент азая бастайды, ол 2.20-суреттегі 3 нүктесіне дәл келеді.

Жалпы қолданыстағы асинхронды қозғалтқыштың ауыспалы кезеңдегі сырғанау S=0,3…0,1 және оның мәні қозғалтқыштың қуаттылығы неғұрлым жоғары болса, соғұрлым төмен (аз) болады. Сол сияқты, тек кері ретпен, асинхронды қозғалтқышты жұмысқа қосқанда, моменті өзгереді; демек сырғанау азайса момент шырқау шегіне дейін өседі, сосын азаяды да жүктеусіз жұмыс моментіне тең моментке нөлдік моментке дейін жақындайды. Асинхронды қозғалтқыш қалыпты жұмыс тәртібі кезінде қалыпты S_Н сырғанауына сәйкес келетін қалыпты М_Н момент дамытады. Жаппай қолданымдағы асинхронды қозғалтқыштар үшін жүргізу моменті мен қалыпты М_Н моменті арасындағы қатынас жүргізу қосу моментінің еселілігі m_n делінеді де мына аралықта болады:

, шырқау шегіндегі моменттің қалыпты моментке қатынасы асинхронды қозғалтқыштың артық жүктемелену қабілеті m_к делінеді: 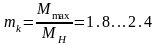бұл асинхронды қозғалтқыштың жағымды қасиеті делінеді. Жүргізу тоғының І_п қалыпты тоққа І_н қатынасын жұмысқа қосу тоғының еселігі і_п дейді, ол мына аралықта болады: 5,5…7,5. Жүргізу қосу тоғының көп болуы, асинхронды қозғалтқыштардың елеулі кемшілігі.

Асинхронды электрқозғалтқыштың жұмысшы дипозондағы механикалық сипаттамасы салыстырмалы түрде "қатаң" сипаттама, демек жұмыс істеу өрісінде оның білігіндегі жүктеменің өзгертуіне қарай айналу жылдамдығы айтарлықтай өзгермейді. Сондықтан асинхронды қозғалтқыштар, негізінен, механизмдер мен машинелерді жүргізуге қолданылады, мұнда айналу жылдамдығы шамамен тұрақты түрде ұстап тұру талап етіледі. Бұл туралы "электржетек" курсында толығырақ қаралады.

Инженерлік тәжрибеде асинхронды қозғалтқыштың жылдамдық сипаттамасын жиі қолданады, онда моменттің сырғанауы емес ротор білігінің айналу жылдамдығына қарайды, демек n₂=ƒ(М) ол қозғалтқыштың айналдырғыш моментінің сипаттамасының өзгеруін білік айналуының функциясы ретінде айқын мағлұмат береді (2.21-сурет). 2.21-суреттегі М_п-жұмысқа қосу моменттері n=0; М_кр=М_mах қозғалтқыш дамытатын моментінің шарықтау шегі (ауысу шегі); М_н- қалыпты момент; n_н- қалыпты айналу жылдамдығы, ол қозғалтқыштың қалыпты жүктемеленуіне сәйкес келеді; n_хх –бос жүріс айналу жылдамдығы; n_с-асинхронды қозғалтыштың магнит өрісінің синхронды айналу жылдамдығы.