МИНОБРНАУКИ РОССИИ

Государственное образовательное учреждение высшего профессионального образования

«Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им.В.И.Ульянова (Ленина)»

(СПбГЭТУ)

Методические указания

к практическим занятиям

В рамках дисциплины «Современный стратегический анализ»

Для подготовки магистров

по направлению 080200 «Менеджмент»

магистерские программы

080251.68 «Менеджмент качества»,

080252.68 «Менеджмент инноваций»,

080253.68 «Антикризисный менеджмент»

и направлению 221400 «Управление качеством»

магистерская программа 221401.68

«Интегрированные системы управления качеством»

Автор

МАРДАС А.Н.

Санкт-Петербург

2011

ББК 65.290-2я7

УДК 65.012.123

Мардас А.Н.

Методические указания к практическим занятиям в рамках дисциплины «Современный стратегический анализ». – СПб: Изд-во СПбГЭТУ, 2011. - с.

ISBN

Методические указания разработаны в соответствии с требованиями Государственного образовательного стандарта к содержанию обучения магистрантов направлений «Менеджмент» и «Управление качеством».

 МАРДАС А.Н.

 Издательство СПбГЭТУ, 2011.

1. План-конспекты практических и семинарских занятий

1.1 Введение в предмет. (Основы системного подхода в стратегическом анализе)

(ПЗ-1 (семинар) – 2 часа)

Учебные цели:

1. Проверить уровень знаний студентов по основам стратегического менеджмента, изученным в ходе бакалаврской подготовки.

2. Обсудить и выработать единые взгляды на содержание и методы системного подхода

Время проведения: 2 часа.

Место проведения и учебно-материальное обеспечение: аудитория, оборудованная мультимедийным видеопроектором.

Указания на подготовку:

а) изучить учебный материал по конспекту лекций и рекомендуемой литературе.

Вопросы, подлежащие обсуждению на семинаре:

1. Сущность и содержание системного подхода.

1.2. Моделирование как метод выбора стратегической альтернативы.

1.3. Управление в сложных системах.

1.4. Эффективность. Показатели и критерии эффективности управления организацией.

Задание на закрепление изученного материала:

1. Опираясь на методологию системного подхода определить систему и формализовать описание проблемы, подлежащей разрешению в будущей выпускной квалификационной работе (ВКР).

2. Осуществить содержательную постановку одной из задач, подлежащих разрешению в ВКР.

3. Оформить письменный отчет в соответствии с требованиями ГОСТа к отчету о НИР.

Рекомендуемая литература

1. Мардас А. Н., Мардас О.А. Организационный менеджмент. – СПб.: Питер, 2003. Глава 1.

2. Котлер Ф. Маркетинг и менеджмент. Анализ, планирование и внедрение. СПб.: Питер, 2004.

3. Мардас А.Н., Кадиев И.Г. Инновационный менеджмент. – СПб.: СПбГЭТУ, 2007.

4. Мардас А.Н. Эконометрический анализ инновационных процессов. СПб.: Изд-во «Элмор», 2007

6. Периодические издания «Инновации», «Менеджмент», «Менеджмент в России и за рубежом» и т.п.

2. Стратегические проблемы развития инновационной экономики России

(ПЗ-2 (семинар) – 2 часа)

Учебная цель:

1. Обсудить и выработать единые взгляды на содержание и методы разработки стратегии инновационного развития России.

Время проведения: 2 часа.

Место проведения и учебно-материальное обеспечение: аудитория, оборудованная мультимедийным видеопроектором.

Указания на подготовку:

а) изучить учебный материал по конспекту лекций, рекомендуемой литературе и методическим указанием на самостоятельную работу;

б) подготовиться к выступлению по вопросам семинара;

в) выполнить реферат в форме эссе объемом до 10 стр. на тему: «Модернизация или инновационное развитие?».

Вопросы, подлежащие обсуждению на семинаре:

1. Стратегические проблемы развития инновационной экономики России.

2. Возможные альтернативы развития инновационной экономики России. Национальные проекты.

Задание на закрепление изученного материала:

Производственная функция – это экономико-математическое выражение зависимости результатов производственной деятельности от обусловивших эти результаты показателей – факторов. Поскольку выбор технологии определяет характер производства, то факторами в производственной функции не являются ни цена, ни норма процента.

В общем виде производственную функцию можно записать следующим образом:

g = f(x) = f(x₁,x₂,…,x_n) (6.1)

где

g - размер выпуска;

x_j - количество j-го фактора.

Наиболее распространены трехфакторные производственные функции, в которых выпуск зависит от затрат труда, капитала и природных ресурсов:

g = f(L,K,M) (6.2)

Кроме того, производственная функция может учитывать время в явном виде, т.е. как особый производственный фактор. В итоге производственные функции разделяются на статические и динамические.

Самой часто упоминаемой в литературе является функция Кобба – Дугласа:

(6.3)

Роль производственной функции (ПФ) в экономической теории определяется тем, что в неоклассических представлениях рациональное ведение хозяйства тождественно максимизации выпуска продукции путем правильного учета технологической связи между затратами и результатом производства.

Определим порядок построения ПФ, отражающей неоклассические представления.

В иллюстративных целях будем считать, что фирма производит только один вид продукции, используя несколько видов затрат. Тогда рациональная фирма должна выбрать вектор x=(x₁,x₂,…,x_n)^T в пространстве неотрицательных затрат

I = {(x₁,x₂,…,x_n)^T | x_j ≥0, j = }, (6.4)

максимизирующий производственную функцию

g = f(x) = f(x₁,x₂,…,x_n) (6.5)

где g - размер выпуска

x_j - количество j-го фактора, j =

Для отражения рациональности производителя ПФ должна обладать определенными содержательными свойствами, переходящими в математические требования к ее построению.

Требование 1 (положительности и полноты ресурсного набора, как пространства переменных функции).

Производство невозможно при отсутствии хотя бы одного ресурса, т.е. строящаяся ПФ должна удовлетворять соотношению f(x) = 0, если x_j = 0. Каждый ресурс необходим хотя бы в малых количествах, и полное его отсутствие не может быть компенсировано другими ресурсами.

Требование 2 (монотонности).

При увеличении затрат производственных ресурсов выпуск продукции не уменьшается:

f(x') ≥ f(x") при x' ≥ x", (6.6)

причем если x' > x", то f(x') > f(x").

Требования 1 и 2 соответствуют выпуклости ресурсного множества, позволяют ввести понятие эффективности производства и определять ее различными подходами по производственной функции.

Основной подход – сопоставление затрат ресурсов и выхода продукции. Отсюда можно вести речь о предельной и средней эффективности как соотношении выхода и затрат в краткосрочном и длительном периодах.

В теории производства принято периоды, которые отличаются друг от друга не с точки зрения их протяжённости во времени (это следует подчеркнуть особо), а с точки зрения того, как изменяется количество используемых фирмой факторов производства за тот или иной промежуток времени.

Постоянные факторы производства – это такие факторы, которые используются фирмой в одном и том же количестве в течение определённого периода времени, т.е. их количество не меняется с изменением объёма выпуска.

Переменные факторы производства – это такие факторы, которые используются фирмой в различных количествах в течение определённого периода времени, т.е. их количество изменяется и в силу этого изменяется объём выпускаемой фирмой продукции.

В краткосрочном периоде технологически процесс производства остается неизменным, т.е. постоянные факторы действительно фиксированы. Издержки производителя тогда растут только за счет увеличения объемов переменных факторов. При этом неизбежно наступает такой момент, когда каждая следующая используемая единица переменного фактора будет вызывать меньшее увеличение выпуска продукции, чем предыдущая. (На уборке картофеля два человека могут выбрать клубней в два раза больше, чем один, т.е. увеличение переменного фактора в два раза увеличивает и выход продукции в два раза. Но очевидно, что привлечение к уборке одиннадцатого человека обеспечит увеличение общего сбора в меньшей степени, чем десятого, и уж тем более, чем второго. Именно в этом проявляется закон убывающей производительности.

Производственная функция должна однозначно отражать отдачу от расширения масштабов производства.

Математически это как раз и означает однородность производственной функции: для любого вектора Х и любого скаляра λ она должна удовлетворять соотношению:

f(λХ) = λⁿ f(Х) (6.11)

Если n > 1, то производственная функция характеризуется возрастающей отдачей от расширения масштабов производства;

если n = 1 – постоянная отдача (наиболее часто встречающийся случай);

при n < 1 – убывающая отдача.

Экономия на масштабе означает рост производительности факторов производства вследствие увеличения фирмой масштаба производственных операций или уменьшение затрат на единицу продукции при увеличении объёма производства. При этом наращивание факторов производства может осуществляться в разных пропорциях. Более того, одни факторы производства могут замещаться другими. Понятие «эффект масштаба», или «отдача от масштаба», предполагает увеличение затрат используемых факторов производства в одинаковое число раз, т.е. предполагает рост объёма выпуска при сохранении неизменной пропорции между используемыми факторами. Таким образом, экономия на масштабе включает в себя и увеличивающийся эффект масштаба производства как частный случай, но в своём более общем виде допускает изменение всех комбинаций вводимых факторов по мере изменения объёма выпуска продукции.

Функция Кобба –Дугласа для двух факторов производства может быть записана как , где a, ,  - константы, определяемые из наблюдаемых данных, Y- выпуск, L - мера услуг (затраты) труда, К- мера услуг (затраты) капитала.

Для данной ПФ предельные продукты труда и капитала могут быть выражены следующим образом:

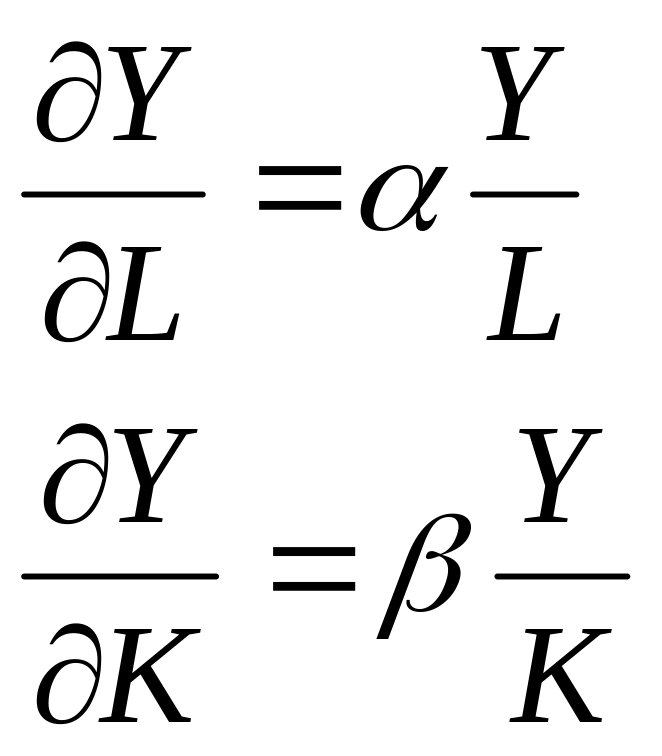(6.22)

Очевидно, что эти выражения являются положительными.

Покажем, что для ПФ Кобба-Дугласа выполняется закон убывающей эффективности (предельные продукты убывают при изменении соответствующего фактора при фиксированных прочих условиях).

Действительно:

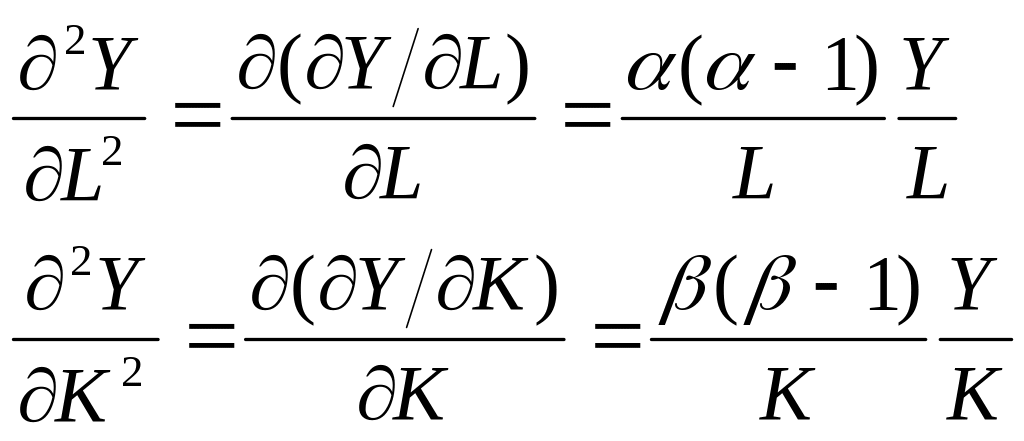, (6.23)

и поскольку  и  обычно меньше единицы, то рассчитываемые вторые производные являются отрицательными, что и свидетельствует о снижении эффективности.

При исчислении предельного продукта труда в (6.22) средний продукт труда домножается на параметр . Разрешим равенство относительно  и получим:

, (6.23)

т.е. показатель степени представляет собой частную эластичность выпуска по затратам труда. Он показывает процентное изменение выпуска, соответствующее однопроцентному изменению затрат труда при неизменности затрат капитала.

Аналогично  является частной эластичностью выпуска по капиталу.

Параметры  и  совместно отражают совокупное процентное изменение выпуска при однопроцентном совокупном изменении затрат труда и капитала. Иначе говоря, математически сумма (+) является степенью однородности производственной функции Кобба – Дугласа и обозначает эффект масштаба производства. Причем отдача при изменении масштаба производства характеризуется следующим образом:

 +  < 1 – потери от изменения масштаба,

 +  = 1 – постоянная (сохраняющаяся) отдача,

 +  > 1 – рост, обуславливаемый экономией на масштабе

При описании экономического роста в теории наиболее часто прибегают к производственным функциям [1]. В классическом варианте производственная функция – это зависимость между количеством используемых ресурсов (факторов производства) и выпуском (объемом выпускаемой продукции) X, причем в качестве ресурсов рассматривают накопленный труд в форме производственных фондов К (капитал) и настоящий (живой) труд L. Тогда экономика описывается двухфакторной производственной функцией, например, в форме Кобба - Дугласа

X= AK^α L^β, (1)

а ее динамика представляется логарифмическим ростом

(2)

для t = 1,2,...,T, где T – длина временного ряда. Если для коэффициентов эластичности выполняется α > β, то имеет место трудосберегающий (интенсивный) рост, в противном случае - фондосберегающий (экстенсивный) рост. Параметр А интерпретируется как параметр технического прогресса, иначе говоря может отождествляться со степенью инновационности экономики: при тех же α и β выпуск в точке (K,L) больше, чем больше А. Таким образом, функция Кобба - Дугласа может стать инструментом управления инвестиционно-инновационным процессом путем выбора коэффициентов эластичности и параметра инновационности A, формирующим соотношение в затратах на факторы производства. Причем, казалось бы, это достижимо в результате исторического анализа эмпирических данных. Однако на этом пути выявляются, как минимум, две трудности.

Во-первых, однозначный расчет (например, методом наименьших квадратов) коэффициентов α, β и А по мультипликативной форме (1) возможен только при однородности производственной функции, что крайне редко выполняется в эмпирических данных.

Во-вторых, регрессионный анализ для обеспечения достоверности результатов требует привлечения выборок со значительными объемами (по оценкам [2] – 500 и более наблюдений), что делает невозможным его непосредственное применение к инновационным, т.е. с минимальной статистикой, процессам.

Первую трудность обычно преодолевают, переходя к удельным величинам x=X/L, k=K/L и допуская α+β=1, что отвечает постоянству отдачи ресурсов. В этом случае соотношения

x_t = Ak_t^α, t = 1,…,T (3)

отражают динамику экономического роста, причем для α=1 именно рост А в исторических данных будет свидетельствовать об инновационном развитии производственно-экономической системы.

Статистика Дарбина-Уотсона свидетельствует в пользу неадекватности модели. Кроме того, для данных за 1922 г (Y₁₉₂₂  = 240; K₁₉₂₂  = 431; L₁₉₂₂  = 161), модель дает y₀ = ln(Y₁₉₂₂ /L₁₉₂₂) = 0,399, когда по реальным данным ln(Y₁₉₂₂ /L₁₉₂₂)=ln(240/161)=0,41.

Ситуация остается неопределенной (DW).

Статистические данные «не пустили» в модель время как заместитель технического прогресса, поскольку переменная К (капитальные затраты) так же является функцией времени, поэтому проявляется мультиколлинеарность.

Возможности преодоления второй трудности основаны на аппарате микростатистики, в свою очередь опирающемся на инвариантные преобразования выборочных данных [4].

В итоге, если эмпирический материал позволяет построить адекватную модель (3), то применение ее к определенным временным интервалам становится инструментом выявления факта (изменение величины A) и предпосылок (соотношение между α и β) инновационного рывка в экономике или некоторой ее подсистеме.

В целом подход к построению прогнозной модели инновационного развития заключается в следующем.

1. По имеющимся эмпирическим данным методами микростатистики (т.е. инвариантными преобразованиями малой выборки) избирается аналитическое представление для кривой экономического роста от начала характерного (т.е. допускающего предположение о старте инновационного процесса) периода.

2. На основе применения супериндикатора (при необходимости с оценкой стохасти­ческого доминирования) оценивается статистическая гипотеза о подчинении выборки эмпирических данных о выпуске X экспоненциальному закону распределения.

3. При отвержении нуль-гипотезы придется отвергнуть и предположение возможностях инновационного роста в рамках сложившейся ресурсно-производственной структуры. Экономический рост следует обеспечивать увеличением объемов привлекаемых факторов производства.

4. Если же нуль-гипотеза принимается, то следует признать, что производственно-экономическая система вступает в стадию инновационного роста и переходить к выбору его рациональных параметров (в нашем случае - А и α) на основе регрессионной модели, приводящей к той же экспоненциальной форме кривой роста.

Применим сформированный подход к современной экономике России.

В качестве материала для анализа будем использовать данные о валовом внутреннем продукте как выпуске X (табл. 1) и численности экономически активного населения как живом труде L в период с 2002 по 2012 год (табл. 2)

[5].

Таблица 1

Темпы роста ВВП России, %

год	значение
2003	7.3
2004	7.2
2005	6.4
2006	8.2
2007	8.5
2008	5.2
2009	-7.8
2010	4.3
2011	4.3
2012	3.6

Источник - CIA World Factbook [5]

­­Таблица 2

Экономически активное население России

Год	Экономически Активные	Занятые	Безработные	Уровень Безработицы, %
2012	75 676 000	71 545 000	4 131 000	5,46
2011	75 779 000	70 857 000	4 922 000	6,50
2010	75 478 000	69 934 000	5 544 000	7,35
2009	75 694 000	69 410 000	6 284 000	8,30
2008	75 700 000	71 003 000	4 697 000	6,20
2007	75 289 000	70 770 000	4 519 000	6,00
2006	74 419 000	69 169 000	5 250 000	7,05
2005	73 581 000	68 339 000	5 242 000	7,12
2004	72 985 000	67 319 000	5 666 000	7,76
2003	72 273 000	66 339 000	5 934 000	8,21
2002	72 357 000	66 659 000	5 698 000	7,88
2001	71 547 000	65 123 000	6 424 000	8,98
2000	72 770 000	65 070 000	7 700 000	10,58

Попытка построить трендовую модель для темпов роста ВВП оказывается несостоятельной ни для линейной, ни для экспоненциальной, ни для иных форм связи. К примеру, для наилучшей обратной модели коэффициент детерминации составил величину 0,138 при статистике Фишера в 1,6. Иначе говоря, отсутствует монотонность в поведении ВВП в период с 2002 по 2013 год, что только подтверждается рис. 1.

Рис. 1. Темпы роста ВВП России

Невозможность построить трендовую модель вынуждает перейти к моделированию по малой выборке, т.е. по данным 2010 - 2012 годов, с использованием разработанного алгоритма идентификации экспоненциального распределения.

Получим:

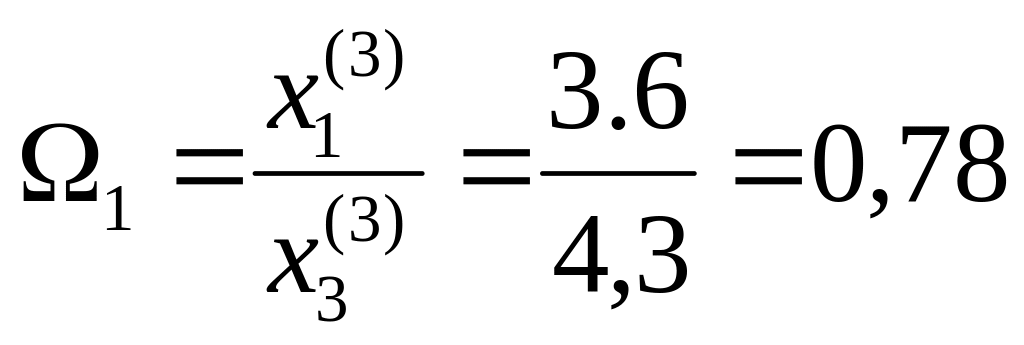
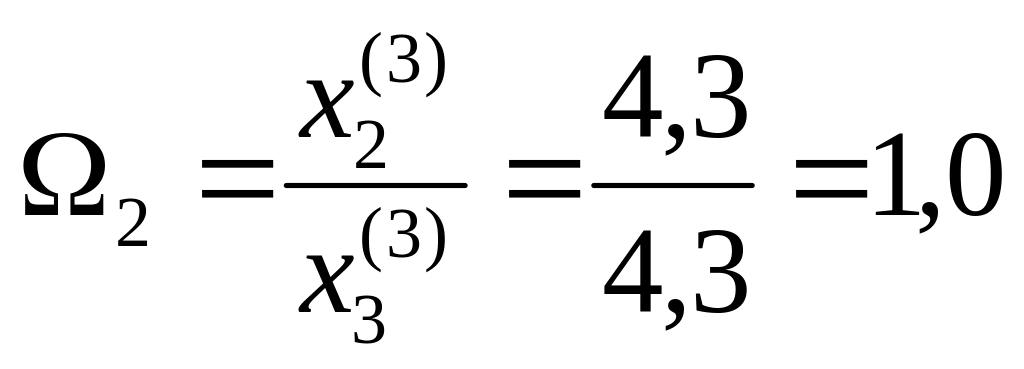
и, соответственно,

Используя табл. 3, можем утверждать, что с доверительной вероятностью в 0,95 гипотеза об экспоненциальном росте ВВП должна была быть отвергнута и даже после преодоления стагфляции речь может идти только о линейной модели развития.

Таблица 3

Критические значения супериндикатора

экспоненциального закона распределения

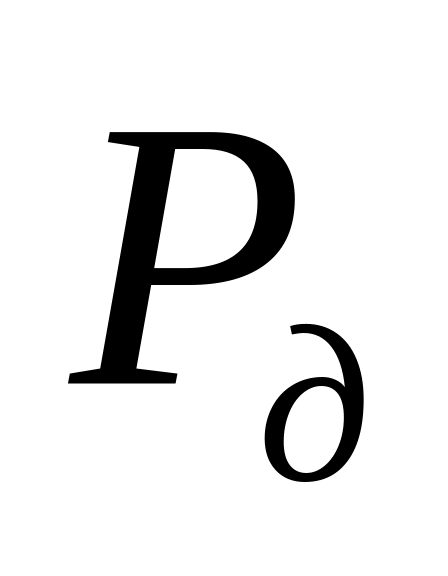
Доверительная. вероятность,	Значения супериндикатора Sкр
	n=2	n=3	n=4	n=5
0,80	0,80	0,454	0,261	0,126
0,85	0,85	0,523	0,307	0,160
0,90	0,90	0,594	0,372	0,222
0,95	0,95	0,713	0,488	0,304
0,975	0,975	0,802	0,588	0,384

Итак, приходится признать, что инновационный прорыв в экономике России в рамках существующего соотношения между фондовооруженностью и производительностью труда практически нереализуем. Столь модные в 2010-2013 годах о вступлении в эру инновационной экономики оказались чистым блефом.

Как изменить эту ситуацию?

В рамках рассматриваемого тестового примера была построена и линейная производственная функция (2) в темповой форме. Эмпирические данные показали незначимость свободного члена, что приводит к дополнительному ограничению А=1 в искомой прогнозной модели Кобба - Дугласа. В итоге из результатов выполненного анализа следует, что нынешняя фондовооруженность промышленности обеспечивает рост экономики России с темпом не более 4,4% только при ежегодном увеличении численности экономически активного населения на 1 млн. человек. При складывающейся демографической ситуации и нынешней миграционной политике в России этого невозможно даже ожидать (табл. 4, рис. 2).

Рис. 2. Динамика численности населения России (млн. чел.) [5]

Выход лежит в структурной перестройке промышленного производства и изменении институциональных условий хозяйствования, а не поисках мифического пятого или шестого «и».

Рекомендуемая литература