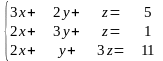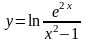Тема 2.2Системы линейных уравнений с n неизвестными.

Цель:отработать навыки решения систем уравнений методом Крамера, Гаусса, матричным методом.

Форма работы: решение задач.

Задания для самостоятельной работы:

1. Найти решение системы уравнений методом Крамера:

1. 

2. 

2. Найти решение системы уравнений методом Гаусса:

1. 

2. 

3. Найти решение системы уравнений матричным методом:

1. 

2. 

Список рекомендуемой литературы:

1. Википедия – свободная энциклопедия http://ru.wikipedia.org/wiki

2. БогомоловН.В., СамойленкоО.Н.Математика//Учебник для техникумов.- М.:

Наука, 2004.

3. ПехлецкийИ.Д..Математика//Учебник для техникумов.- М.: Наука, 2001.

4. Щипачев В.С.. Основы высшей математики. – М.: Высшая школа, 2001.

Порядок проверки, защиты самостоятельной работы:

проверка рабочей тетради.

Тема 3.1 Производная и дифференциал.

Цель:отработать навыки вычисления пределов функций, производных функций.

Форма работы: решение задач.

Задания для самостоятельной работы:

1. Найти предел функции, не используя правило Лопиталя:

2.Найти производную функций:

Список рекомендуемой литературы:

1. Википедия – свободная энциклопедия http://ru.wikipedia.org/wiki

2. БогомоловН.В., СамойленкоО.Н.Математика//Учебник для техникумов.- М.: Наука, 2004.

3. Данко П.Е., Попов А.Г., Коженикова Т.Я. Высшая математика в упражнениях и задачах. Часть1 и 2. – М.: Высшая школа, 1999.

4. ПехлецкийИ.Д..Математика//Учебник для техникумов.- М.: Наука, 2001.

5. Альхова З.Н., Макеева А.В. Внеклассная работа по математике.- Саратов, 2001.

6. Выгодский М.Я. Справочник по высшей математике. – М.: Росткнига, 2001.

7. Казанджан Э. П., Холмская Г. С. «Интегрирование. Методика решений.

Учебное пособие для вузов», М.: Дрофа, 2010

8. Щипачев В.С.. Основы высшей математики. – М.: Высшая школа, 2001.

Порядок проверки, защиты самостоятельной работы:

проверка рабочей тетради.

Тема 3.2. Приложения производной.

Цель:обобщить схему исследования функций и построение графиков функций по данным исследованиям; развивать умения применять полученные знания при решении задач на нахождение наибольшего и наименьшего значений, составлении уравнений касательной и нормали к кривой.

Форма работы: решение задач.

Задания для самостоятельной работы:

1.Составить уравнение касательной и нормали к кривой:

1. в точке ;

2. в точке ;

2. Для указанной функции требуется провести полное исследование функции и построить её график.

1. .

3.Найти наибольшее и наименьшее значения функции на отрезке .

1. , [0; 2];

2. , [-2; 1];

3. , [0,5; 2].

Схема решения задачи на оптимизацию (нахождения наибольшего и наименьшего значений величин):

• проанализировав условие задачи, выделите оптимизируемую величину;

• одну из участвующих в задаче неизвестных величин принять за независимую переменную и установить реальные границы ее изменения в соответствии с условиями задачи;

• исходя из условия задачи, составить функцию подлежащую исследованию, выразив оптимизируемую величину через независимую переменную и известные величины;

• для полученной функции найти наибольшее или наименьшее в зависимости от условия значение в промежутках реального изменения аргумента;

• исходя из результатов исследований, записать ответ в терминах предложенной задачи.

4. Решить задачи на оптимизацию.

Сварщики получили задание из металлического стержня длиной а, необходимо согнуть скобу прямоугольной формы и приварить её к металлической балке. Как выбрать на стержне точки сгиба, чтобы площадь образовавшегося прямоугольника была наибольшей?

Список рекомендуемой литературы:

1. Википедия – свободная энциклопедия http://ru.wikipedia.org/wiki

2. БогомоловН.В., СамойленкоО.Н.Математика//Учебник для техникумов.- М.: Наука, 2004.

3. Данко П.Е., Попов А.Г., Коженикова Т.Я. Высшая математика в упражнениях и задачах. Часть1 и 2. – М.: Высшая школа, 1999.

4. ПехлецкийИ.Д..Математика//Учебник для техникумов.- М.: Наука, 2001.

5. Щипачев В.С.. Основы высшей математики. – М.: Высшая школа, 2001.

Порядок проверки, защиты самостоятельной работы:

проверка рабочей тетради.