2.2 Интервальные оценки

Интервальные оценки - это оценки, которые с доверительной вероятностью γ в некотором интервале содержат истинное значение числовой характеристики:

Р (и<и<и) = γ, (2.9)

где и и и - соответственно нижняя и верхняя доверительные границы

интервала значений оцениваемой характеристики;

θ – истинное значение характеристики.

Для получения интервальных оценок необходимо знать закон распределения случайной величины.

Если показатель надежности подчиняется экспоненциальному закону распределения, то интервальную оценку этого показателя определяют из неравенства (2.10):

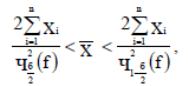(2.10)

где и - квантили распределения, соответствующие вероятностям и и числу степеней свободы f = 2n, определяемые по таблице Б1 приложения Б.

Пример 3 Определим интервальную оценку математического ожидания из примера 1 при условии, что описываемая случайная величина подчиняется экспоненциальному закону.

Принимаем значение доверительной вероятности γ = 0,95, тогда

α = 1- γ = 0,05.

Тогда число степеней свободы f=2·15=30.

Этим значениям соответствуют квантили =46,97924 и

=16,79077, принятые по таблице Б1 приложения Б.

Так как значение математического ожидания известно, то для упрощения расчетов приведем формулу (2.10) к виду:

Таким образом, если случайная величина подчиняется экспоненциальному закону, то математическое ожидание времени исправного состояния рулевого управления автобуса «Autosan» находится в интервале 25,3 - 70,9 тыс. км.

Если показатель надежности подчиняется нормальному закону распределения, то интервальную оценку этого показателя определяют из неравенства:

(2.11)

где X и S – оценки математического ожидания и дисперсии; t ;f - квантиль распределения Стьюдента, соответствующая доверительной вероятности γ = 1 – α и числу степеней свободы f = n-1, определяемые по таблице Б2 приложения Б.

Пример 4 Определим интервальную оценку математического ожидания из примера 1 при условии, что описываемая случайная величина подчиняется нормальному закону.

При значении доверительной вероятности γ=0,95 и f=15-1=14 определим квантиль распределения Стьюдента по таблице Б2 приложения Б,

Если случайная величина подчиняется нормальному закону, то математическое ожидание времени исправного состояния рулевого управления автобуса «Autosan» находится в интервале 32,9 - 46,5 тыс. км.

3 Графическое представление случайной величины

Для определения вида закона распределения случайной величины удобно представить данные наблюдений в графическом виде. Для графического представления данных наблюдения используется специальный график – гистограмма (рисунок 3.1).

Рисунок 3.1 – Гистограмма и полигон распределения

Гистограмма является важным вспомогательным средством при принятии гипотезы о виде функции распределения. Поэтому необходимо извлечь из нее максимум информации. Дело в том, что форма гистограммы зависит от числа и величины интервалов разбиения. При слишком малом числе интервалов разбиения (интервал велик), плохо выявляются характерные особенности распределения. С ростом числа интервалов характерные особенности выявляются все лучше, но лишь до определенного предела. При большом числе интервалов (интервал слишком мал) гистограмма снова теряет характерные особенности распределения, превращаясь в пределе (когда в каждом интервале не более одного значения) в чередование "пустых" интервалов и одинаковых по высоте прямоугольников.

Наиболее простой способ разбиения вариационного ряда - это использование равновеликих интервалов, количество которых определяется по специальным формулам, например, по формуле (2.6).

Согласно этому правилу при объеме выборки до тысячи полных реализаций рекомендуемое число интервалов разбиения не превышает одиннадцати. Для объемов выборки n < 50, с которыми в основном приходится иметь дело при обработке результатов испытаний на надежность, вид гистограмм слишком чувствителен к способу разбиения, поэтому правило (2.6) можно использовать лишь как ориентировочное. В этих случаях рекомендуется построить несколько вариантов гистограмм для различных способов разбиения вариационного ряда – для k = 6,7,8 и т.д.

При построении гистограммы по оси абсцисс откладывают в выбранном масштабе интервалы, и, взяв их как основания, строят прямоугольники, высота которых равна статистической плотности распределения на интервале. Построенная таким образом ступенчатая функция fj называется гистограммой выборки. Эта функция служит статистическим аналогом плотности распределения вероятности случайной величины и на j-ом интервале определяется по формуле 3.1

f_j = m_j / (n·Δx). (3.1)

Площадь гистограммы равна единице.

Если соединить прямыми линиями середины верхних (горизонтальных) сторон прямоугольников гистограммы, то получится полигон распределения в виде ломаной линии (рисунок 3.1).

При построении нескольких гистограмм с разным количеством интервалов лучшей нужно считать гистограмму, имеющую меньшее число инверсий. Признаком инверсии считается изменение знака приращения высоты прямоугольника. Если число инверсий одинаково, лучшей следует считать ту, которая имеет большее число интервалов.

По данным статистического ряда можно вычислить еще одну характеристику случайной величины - эмпирическую интегральную функцию распределения. Значение эмпирической интегральной функции распределения для j-ого интервала Fj определяется по формуле:

(3.2)

Функция распределения F(x) может быть представлена в виде графика, который строится подобно гистограмме, только высоты прямоугольников равны значениям функции распределения соответствующих интервалов.

Пример графика приведен на рисунке 3.2.

Рисунок 3.2 – График эмпирической интегральной функции

распределения опытных данных

Интегральная функция распределения является более универсальной характеристикой распределения по сравнению с гистограммой, которая определяет вероятность того события, что случайная величина X будет меньше или равна заданному значению x. Эмпирическая интегральная функция распределения определяет частость (опытную вероятность) события X ≤ x.

Пример 5 Построим гистограмму и график интегральной функции распределения для данных из примера 2.

В качестве первого приближения принимаем число интервалов, рассчитанное по формуле Стенжерса.

Принимаем число интервалов k = 6, ширина интервала Δx = 43,3.

Рисунок 3.3

В этом случае имеем одну инверсию (при переходе с 5 на 6 интервал).

Принимаем число интервалов k = 7, ширина интервала Δx = 37,13.

Расчеты сведены в таблицу 3.1.

Таблица 3.1 – Подсчет частот

Номер интервала	Границы интервалов	Середина интервала, xj	Число попаданий, mj
1	70 -107,1	88,6	1
2	107,1 -144,3	125,7	1
3	144,3-181,4	162,8	4
4	181,4 -218,5	200,0	9
5	218,5-255,6	237,1	11
6	255,6-292,8	274,2	15
7	292,8-329,9	311,3	4

Рисунок 3.4

В этом случае опять получаем одну инверсию.

Принимаем число интервалов k = 8, ширина интервала Δx = 32,5

Расчеты сведены в таблицу 3.2

Таблица 3.2 – Подсчет частот

Номер интервала	Границы интервалов	Середина интервала, xj	Число попаданий, mj
1	70 -102,5	86,24	1
2	102,5-135	118,7	1
3	135-167,5	151,2	3
4	167,5 -200	183,7	7
5	200-232,4	216,2	9
6	232,4-264,9	248,7	10
7	264,9-297,4	281,2	11
8	297,4-329,9	313,7	3

Рисунок 3.5

И в этом случае получаем одну инверсию.

Принимаем число интервалов k = 9, ширина интервала Δx = 28,9.

Расчеты сведены в таблицу 3.3.

Таблица 3.3 – Подсчет частот

Номер интервала	Границы интервалов	Середина интервала, xj	Число попаданий, mj
1	70 -98,88	84,4	1
2	98,88-127,8	142,2	0
3	127,8-156,6	200,0	3
4	156,6-185,5	257,7	4
5	185,5-214,4	315,5	7
6	214,4-243,3	373,2	9
7	243,3-272,1	431,0	12
8	272,1-301	488,7	7
9	301-329,9	315,5	2

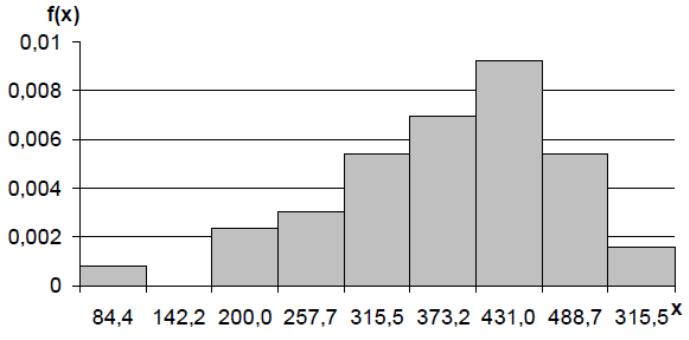
Рисунок 3.6

В данном случае имеем две инверсии (при переходе с 1 на 2 интервал и с 7 на 8). Таким образом принимаем количество интервалов, равное 8, т.к. количество инверсий минимально, а количество интервалов наибольшее.