2.3.2. Закон Малюса

В 1809 г. французский инженер Э. Малюс открыл закон, названный впоследствии его именем. В опытах Малюса свет последовательно пропускался через две одинаковые пластинки из турмалина. Пластинки могли поворачиваться друг относительно друга на угол φ (рис. 16).

Рисунок 16 - Прохождение естественного света последовательно через два идеальных поляроида

Интенсивность прошедшего света оказалась прямо пропорциональной: : . (20)

Ни двойное лучепреломление, ни закон Малюса не нашли объяснения в рамках теории продольных волн. Для продольных волн направление распространения луча является осью симметрии. В продольной волне все направления в плоскости, перпендикулярной лучу, равноправны. В поперечной волне (например в волне, бегущей по резиновому жгуту) направление колебаний и перпендикулярное ему направление не равноправны (рис. 16.1).

Рисунок 16.1 – Волна бегущая по резиновому жгуту

Из рисунка видно, что поворот щели S вызовет затухание волны. С помощью разложения вектора   на составляющие по осям можно объяснить закон Малюса (рис. 16). В каждый момент времени вектор   может быть спроектирован на две взаимно перпендикулярные оси (рис. 16.2).

Рисунок 16.2 – Проекции вектора

Рассмотрим прохождение естественного света последовательно через два идеальных поляроида Р и А (рис. 16), разрешенные направления которых развернуты на некоторый угол φ. Первый поляроид играет роль поляризатора. Он превращает естественный свет в линейно-поляризованный. Второй поляроид служит для анализа падающего на него света. Здесь также используется явление дихроизма. Световую волну с амплитудой   разложим на две составляющие.

, , (21)

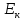         – пройдет через поляризатор, а 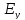  – не пройдет.

Найдем интенсивность проходящего света. Т.к.  , то   и 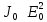 , отсюда получим закон Малюса:

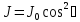  (22)

В естественном свете все значения φ равновероятны и среднее значение 

. Поэтому интенсивность естественного света, прошедшего один поляризатор уменьшается в два раза. Поставим на пути естественного света два поляризатора, плоскости которых образуют угол φ. Из первого поляризатора выйдет луч интенсивностью . Согласно закону Малюса интенсивность света, прошедшего второй поляризатор,   (23)

Это без учета поглощения света в кристалле.

    при φ = 0 (24)

При φ = π/2,   – скрещенные поляризаторы свет не пропускают. Таким образом, в электромагнитной теории света закон Малюса находит естественное объяснение на основе разложения вектора   на составляющие.

2.3.3. Закон Брюстера

Когда световая волна падает на границу раздела двух прозрачных диэлектриков, она испытывает отражение и преломление. Для расчета амплитуд отражений и преломлений волн пользуются формулами Френеля. Так в случае отраженной волны амплитуды компонент вектора Е имеют вид (рис. 17 и формулы 25 и 25.1):

Рисунок 17 - Закон Брюстера 

(25)

(25.1)

Из (25) и (25.1) вытекает, что если , то тогда  и , но  и . В отраженном свете присутствуют колебания только вектора , а это означает, что отраженный свет линейно поляризован. Таким образом, при выполнении условия Брюстера, отраженный свет будет полностью поляризован в плоскости, перпендикулярной плоскости падения. Это утверждение носит название закона Брюстера. Оно реализуется тогда и только тогда, когда угол между отраженной и преломленной волнами равен  . Это соответствует определенному углу падения , называемому углом Брюстера. Его значение можно рассчитать так:  .

Закон Брюстера имеет простое объяснение. Отраженная световая волна появляется за счет излучения электронов среды, совершающих вынужденные колебания под действием вектора преломленной волны. Это излучение имеет направленный характер: его интенсивность равна нулю в направлении колебаний зарядов. Направим под углом Брюстера на границу раздела плоско поляризованную волну с вектором , лежащим в плоскости падения.

Рисунок 18 – Диаграмма направления излучения, возбужденного вектором

Нулевой минимум этой диаграммы при выполнении условия Брюстера совпадает по направлению с отраженным лучом. Если вектор  падающей волны направить перпендикулярно плоскости падения (рисунок ниже), то направление колебаний электронов будет перпендикулярно плоскости падения. Тогда диаграмма направленности будет развернута своим максимумом в направлении отраженного луча (рис. 19). Напомним, что пространственная форма диаграммы похожа на бублик без дырки.

Рисунок 19 - Диаграмма направленности развернута своим максимумом в направлении отраженного луча