Министерство образования Республики Беларусь

Учреждение образования

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Факультет информационных технологий и управления

Кафедра ИТАС

ОТЧЕТ

по лабораторной работе №4

“ Моделирование многомерных случайных чисел”

по дисциплине «Статистические методы обработки данных»

Выполнила:	Проверил:
студентка гр. 920604	ассистент
А. П. Голубова	А.Ф. Трофимович

Минск 2012

1. Цель работы

1.1. Изучение методов моделирования многомерных случайных чисел.

1.2. Приобретение навыков моделирования многомерных случайных чисел в системе Matlab.

2. Ход работы

Создадим 3 файла-функции, аналогично лабораторной работе №3, которые будут генерировать случайные числа по трём распределениям: Нормальное, Хи-квадрат, экспоненциальное, и файл-функцию для построения диаграмм рассеяния.

Файл normal.m (нормальное распределение):

function f = normal(a,sigma)

c=2*pi;

r =sqrt(-2*log(rand));

fi=c * rand;

e1=r * cos(fi);

f=a+sigma*e1;

end

Файл h.m (распределение хи-квадрат):

function y = h(x)

sum = 0;

for i = 1 : x

sum = sum + normal(0,1)^2;

end

y=sum;

end

Файл eksp.m (экспоненциальное распределение):

function [ y ] = eksp( lambda)

a =rand;

y = -lambda * log(a);

end

Файл graph.m (построение диаграмм рассеяния):

function graph(x1,x2,y1,y2)

hold on

plot(x1,y1,'r.',x2,y2,'b.');

legend('Function','MATLAB',1);

grid;

end

Создадим главный программный файл для исследования распределений (Untitled3.m):

clear;

clc;

figure;

n=100;

a1=0;

a2=0;

sigm1=0.01;

sigm2=10;

sigm=[sigm1^2 0; 0 sigm2^2];

mu=[a1 a2];

for i=1:n

x(i)=normal(a1,sigm1);

y(i)=normal(a2,sigm2);

end

r12=corrcoef(x,y);

nr=mvnrnd(mu,sigm,n);

subplot(131);

graph(x,nr(:,1),y,nr(:,2));

title('Нормальное распределение');

hold on

reg1=a2+r12(1,2)*(sigm2/sigm1)*(x-a1);

reg2=a1+r12(1,2)*(sigm1/sigm2)*(y-a2);

subplot(131);

plot(x,reg1,'g');

grid;

plot(reg2,y,'y');

grid;

k=10;

for i=1:n

x(i)=h(k);

y(i)=h(k);

xx(i)=chi2rnd(k);

yy(i)=chi2rnd(k);

end

subplot(132);

graph(x,xx,y,yy);

axis([-1,12,-1,15]);

title('Хи-квадрат распределение');

lambda=1;

for i=1:n

x(i)=eksp(lambda);

y(i)=eksp(lambda);

xx(i)=exprnd(lambda);

yy(i)=exprnd(lambda);

end

subplot(133);

graph(x,xx,y,yy);

axis([-1,12,-1,15]);

title('Экспоненциальное распределение');

hold off

Исследуем влияние коэффициентов на функции распределений.

1. (рисунок 1)

Рисунок 1 – Исследование распределений (опыт 1)

2. (рисунок 2)

Рисунок 2 – Исследование распределений (опыт 2)

(рисунок 3)

Рисунок 3 – Исследование распределений (опыт 3)

Вывод:

Коэффициенты и управляют смещением «облака» значений случайных чисел относительно начала координата, а коэффициенты и – max и min значениями случайных чисел по осям X и Y соответственно для нормального распределения.

Коэффициент 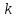управляет группированием «облака» значений случайных чисел относительно начала координата для распределения Хи-квадрат (при увеличении, плотность скопления возле начала координат уменьшается) и распределения Фишера (при увеличении, плотность скопления возле начала координат увеличивается).

Коэффициент управляет плотностью группирования значения экспоненциального распределения.