СМОД – Статистические методы обработки данных / Лаба 1 - 8 / smodlabs / по смоду / шпоры_2006г / 11

11.Метод максимума апостериорной плотности вероятности.

Он отличается от метода макс. правдоподобия постановкой задач. Как и в предыдущем методе считается известна с точностью плотность вероятности . Параметр –случайный вектор, который принял на время извлечения выборки какое-то значение, которое и требуется оценить.

Известна плотность вероятности вектора это

Требуется по выборке найти оценку

Эта задача относится к классу байесовских задач. Она характеризуется тем, что считается известными распределения неизвестных величин.

Метод состоит в том, что оценка отыскивается из условия максимальной апостериорной плотности вероятности:

Можно максимизировать логарифмич. апостериорную плотность вероятности:

Апостериорная плотность вероятности определяется по формуле Байеса:

,

Т.к. знаменатель в формуле Байеса не зависит от параметра , то он не влияет на результат максимизации апостериорной плотности вероятности достаточно решать задачу

или

Учитывая выражение функций правдоподобия и необходимые условия экстремума функций многих переменных получаем для нахождения оценок следующую систему уравнений:

;

Сравниваем эту систему с системой по методу максимума. правдоподобия замечаем, что она отличается наличием первого слагаемого. Это слогаемое зависит от апреорной плотности вероятности и позволяет учитывать апреорную информацию по параметру.

Пример: найти оценку параметра сдвига a в считая - известна. Воспользуемся методом макс. апостериорной плотности вероятности в предположении, что а распределен по нормальному закону , -априорное мат. ожидание.

Решение:

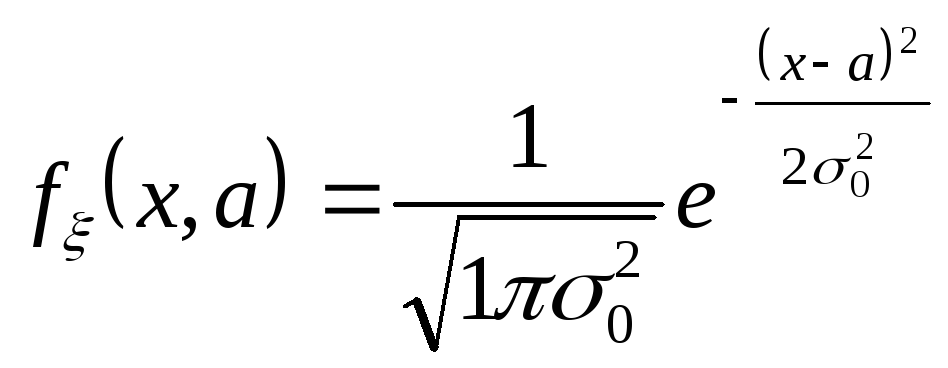
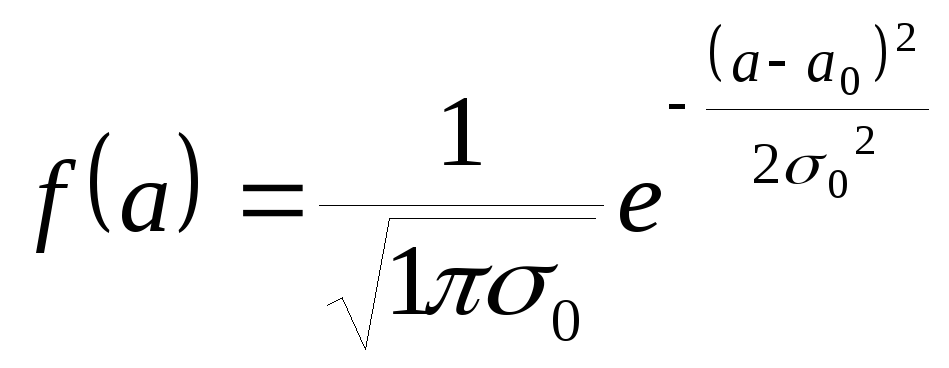
получаем уравнение:

- оценка по методу максимума апостериорной вероятности

Для анализа этой оценки преобразуем ее к другому виду. Для этого разделим числитель и знаменатель на :

Видно, что априорные данные , т.е. имеет вес и каждое наблюдение взвешивается с весом .эти данные суммируются со своими весами. Полученный результат на сумму всех весов. Вес-это степень доверия к данным.

При увеличении объема выборки величина станет значительно меньше величины и можно будет отбросить. В результате при большом получим:

,

При увеличении объема выборки апостериорной плотности вероятности приближается к Мп оценке, т.е. априорные данные учитываются с меньшим весом.