Министерство образования Республики Беларусь

Учреждение образования

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Факультет информационных технологий и управления

Кафедра ИТАС

ОТЧЕТ

по лабораторной работе №4

«Моделирование многомерных случайных чисел»

по дисциплине «Статистические методы обработки данных»

Выполнили:	Проверил:
студенты гр. 020603
Зеленовский Д. А. Владыко Д. П.	Муха В. С.

Минск 2013

1. Цель работы

Изучение методов моделирования многомерных случайных чисел. Приобретение навыков моделирования многомерных случайных чисел в системе Matlab.

2. ЗАДАНИЕ

2.1. Выполнить моделирование двухмерных случайных чисел с указанными распределениями. Для каждого распределения вывести диаграмму рассеивания, на которую нанести 100…500 случайных чисел, используя собственную программу, реализующую предложенный алгоритм, и стандартную программу Matlab.

2.2. На диаграмму рассеивания двухмерного нормального распределения вывести также функцию регрессии

.

Здесь – математическое ожидание и среднее квадратичное отклонение аргумента, – математическое ожидание и среднее квадратичное отклонение функции, – коэффициент корреляции между аргументом и функцией.

2.3. Исследовать изменение диаграмм рассеивания в зависимости от параметров распределений.

3. Ход работы

3.1. Многомерное нормальное распределение

Нормальное распределение с коэффициентами , представлено на рисунке 1.

Рисунок 1

Нормальное распределение с коэффициентами , представлено на рисунке 2.

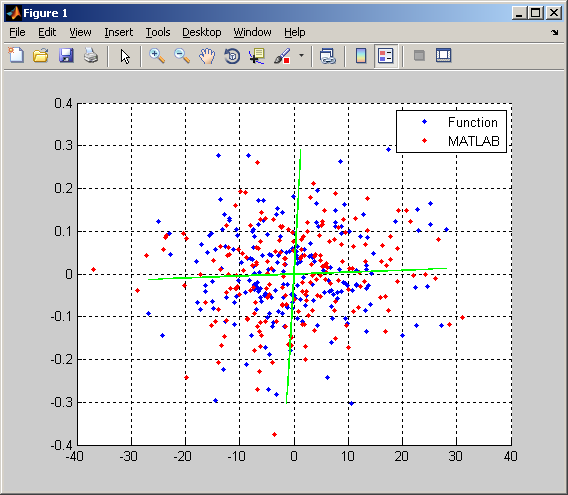
Рисунок 2

Нормальное распределение с коэффициентами , представлено на рисунке 3.

Рисунок 3

3.2 Многомерное распределение Фишера

Распределение Фишера с коэффициентами , представлено на рисунке 4.

Рисунок 4

Распределение Фишера с коэффициентами , представлено на рисунке 5.

Рисунок 5

4. ВЫВОД

Для нормального распределения и распределения Фишера было выполнено моделирование двухмерных случайных чисел. Для каждого распределения выведена диаграмму рассеивания, на которую нанесено 200 случайных чисел, используя собственную программу и стандартную программу Matlab. Кроме того, на диаграммах рассеивания двухмерного нормального распределения выведена функция регрессии.

Было исследовано изменение диаграмм рассеивания в зависимости от параметров распределений.

ПРИЛОЖЕНИЕ

Функция для построения диаграмм рассеяния:

function graph(x1,x2,y1,y2)

hold on

plot(x1,y1,'b.',x2,y2,'b.');

grid;

end

Функция для построения нормального распределения:

function f = normal(a,sigma)

c=2*pi;

r =sqrt(-2*log(rand));

fi=c * rand;

e1=r * cos(fi);

f=a+sigma*e1;

end

Функция для построения распределения Фишера:

function y = fshr(k, m)

v = h(m);

w = h(k);

y = (v / m) / (w / k);

end

function y = h(x)

sum = 0;

for i = 1 : x

sum = sum + normal(0,1)^2;

end

y=sum;

end

Главный файл для построения нормального распределения:

clear;

clc;

n=200;

a1=0;

a2=0;

sigm1=1;

sigm2=1;

sigm=[sigm1^2 0; 0 sigm2^2];

mu=[a1 a2];

for i=1:n

x(i)=normal(a1,sigm1);

y(i)=normal(a2,sigm2);

end

r12=corrcoef(x,y);

nr=mvnrnd(mu,sigm,n);

graph(x,nr(:,1),y,nr(:,2));

hold on

reg1=a2+r12(1,2)*(sigm2/sigm1)*(x-a1);

reg2=a1+r12(1,2)*(sigm1/sigm2)*(y-a2);

plot(x,reg1,'r');

grid;

plot(reg2,y,'r');

grid;

Главный файл для построения рассеяния Фишера:

clear;

clc;

n=200;

k=200;

m=400;

for i=1:n

x(i)=fshr(k,m);

y(i)=fshr(k,m);

xx(i)=frnd(m,k);

yy(i)=frnd(m,k);

end

graph(x,xx,y,yy);

hold off