Министерство образования Республики Беларусь

Учреждение образования

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Факультет информационных технологий и управления

Кафедра ИТАС

ОТЧЕТ

по лабораторной работе №5

“Оценивание законов распределения скалярных случайных величин”

по дисциплине «Статистические методы обработки данных»

Выполнила:	Проверил:
студентка гр. 920604	ассистент
А. П. Голубова	А.Ф. Трофимович

Минск 2012г.

1. Цель работы

- Изучение оценок законов распределения скалярных случайных вели-чин

- Приобретение навыков получения оценок законов распределения ска-

лярных случайных величин с помощью системы программирования Matlab.

2. Ход работы

2.1 Нормальное распределение :

,

Для получения выборок нормального распределения, используя функции получения случайного числа с заданным распределением из лабораторной работы 3, составим программу:

clc;

x = [];

x1 = [];

a = 0;

sigma = 1;

y = x;

y1 = x;

n = 100;

hold on;

for i = 1 : n

x(i) = normal(a,sigma);

y(i) = i / n;

end

Для получения гистограммы и генеральной плотности распределения, используем следующий код, результат представлен на рисунках 2.1, 2.2:

x = sort(x);

minx = min(x);

maxx = max(x);

x1 = minx : 0.1 : maxx;

y1 = normcdf(x1,a,sigma);

plot(x1,y1,'-r');

stairs(x,y);

hold off;

figure;

hold on;

hist(x,10);

y1 = normpdf(x1,a,sigma);

y1 = y1 * n * (maxx - minx) / 10;

plot(x1,y1,'-r');

Рисунок 2.1 – Совместный график гистограммы и генеральной плотности распределения

Для исследования сходимости эмпирической функции распределения к генеральной изменяем объем выборки в 10, 100 раз от первоначального объема. Результат представлен на рисунках 2.3, 2.4

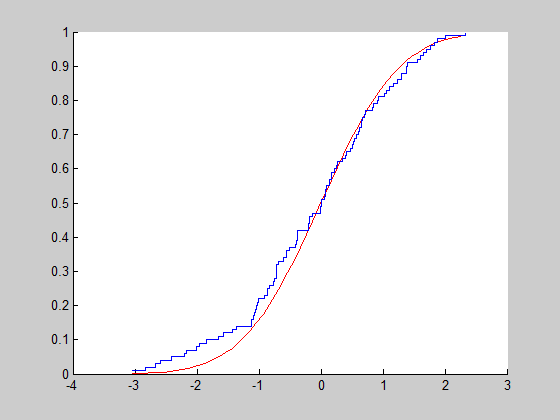
Рисунок 2.2 – Совместный график эмпирической и генеральной функции распределения

Рисунок 2.3 – Совместный график эмпирической и генеральной функции распределения при объеме выборки равном 1000

Рисунок 2.4 – Совместный график эмпирической и генеральной функции распределения при объеме выборки равном 10000

2.2 Распределение с 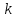степенями свободы :

где

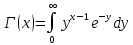
Для получения выборок распределения , используя функции получения случайного числа с заданным распределением из лабораторной работы 3, составим программу:

clc;

x = [];

x1 = [];

k = 10;

y = x;

y1 = x;

n = 100;

hold on;

for i = 1 : n

x(i) = h(k);

y(i) = i / n;

end

Для получения гистограммы и генеральной плотности распределения, используем следующий код, результат представлен на рисунках 2.5, 2.6:

x = sort(x);

minx = min(x);

maxx = max(x);

x1 = minx - 5 : 0.1 : maxx;

y1 = chi2cdf(x1,k);

plot(x1,y1,'-r');

stairs(x,y);

hold off;

figure;

hold on;

hist(x,10);

y1 = chi2pdf(x1,k);

y1 = y1 * n * (maxx - minx) / 10 ;

plot(x1,y1,'-r');

Рисунок 2.5 – Совместный график гистограммы и генеральной плотности распределения

Рисунок 2.6 – Совместный график эмпирической и генеральной функции распределения

Для исследования сходимости эмпирической функции распределения к генеральной изменяем объем выборки в 10, 100, 500 раз от первоначального объема. Результат представлен на рисунках 2.7 – 2.9

Рисунок 2.7 – Совместный график эмпирической и генеральной функции распределения при объеме выборки равном 1000

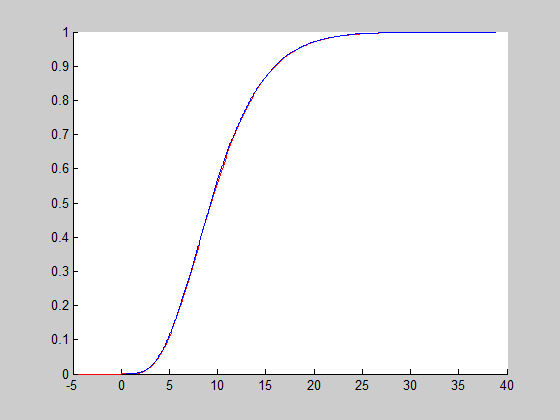
Рисунок 2.8 – Совместный график эмпирической и генеральной функции распределения при объеме выборки в 10000

Рисунок 2.9– Совместный график эмпирической и генеральной функции распределения при объеме выборки в 50000

2.3 Экспоненциальное распределение:

Для получения выборок экспоненциального распределения, используя функции получения случайного числа с заданным распределением из лабораторной работы 3, составим программу:

clc;

x = [];

x1 = [];

lambda = 10;

y = x;

y1 = x;

n = 100;

hold on;

for i = 1 : n

x(i) = eksp(lambda);

y(i) = i / n;

end

Для получения гистограммы и генеральной плотности распределения, используем следующий код, результат представлен на рисунках 2.10 – 2.11:

x = sort(x);

minx = min(x);

maxx = max(x);

x1 = minx - 5 : 0.1 : maxx;

y1 = expcdf(x1,lambda);

plot(x1,y1,'-r');

stairs(x,y);

hold off;

figure;

hold on;

hist(x,10);

y1 = exppdf(x1,lambda);

y1 = y1 * n * (maxx - minx) / 10 ;

plot(x1,y1,'-r');

Рисунок 2.10 – Совместный график эмпирической и генеральной функции распределения

Рисунок 2.11 – Совместный график гистограммы и генеральной плотности распределения

Для исследования сходимости эмпирической функции распределения к генеральной изменяем объем выборки в 10, 100 раз от первоначального объема. Результат представлен на рисунках 2.12 – 2.13.

Рисунок 2.12– Совместный график эмпирической и генеральной функции распределения при объеме выборки равном 1000

Рисунок 2.13– Совместный график эмпирической и генеральной функции распределения при объеме выборки в 10000

Вывод:

Выполнив лабораторную работу, доказали на практике сходимость эмпирического распределения к генеральному при увеличении объема выборки. Построили гистограммы и эмпирические функции распределения. Из гистограмм, при незнании закона распределения, можно сделать предположение о принадлежности выборки к определенному закону распределения.