Занятие 12 Активные четырехполюсники
Изучите теоретический материал по учебной литературе: [1, с.181–183] и ответьте на следующие вопросы:
Какие четырехполюсники называются активными?
С помощью каких идеальных элементов цепи представляют на схемах замещения передаточные параметры активных четырехполюсников?
Какие системы параметров чаще применяются для описания свойств активных четырехполюсников?
Модели каких физических приборов представляются с помощью активных четырехполюсников?
Какие типы зависимых источников используются в электрических схемах?
Какие характерные отличия матриц параметров идеальных зависимых источников от матриц параметров пассивных четырехполюсников?
Как можно представить идеальные зависимые источники в виде четырехполюсников?
Чем отличаются коэффициенты
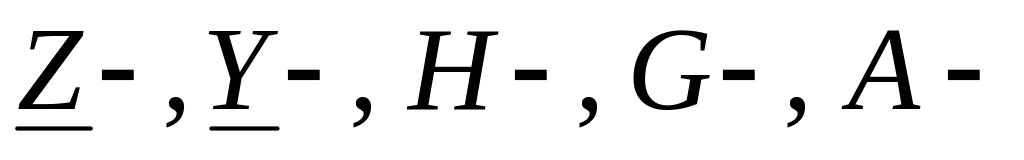параметров
активных четырехполюсников от
соответствующих коэффициентов пассивных
четырехполюсников?
В качестве подготовительного задания рекомендуется решить задачу 12.1.
При решении задач на определение коэффициентов передачи по напряжению следует учесть, что при принятых для Н–параметров условных положительных направлениях (рис. 12.1).
;
,
где
.
Рис. 12.1. Схема к задаче 12.4
Если
рассчитывается коэффициент усиления
для усилительного каскада, то следует
иметь в виду, что этот расчет ведется
для переменной составляющей. Для этого
при составлении расчетной схемы
замыкаются накоротко источники
постоянного напряжения питания и
напряжения смещения.
З а д а ч а 12. 1
По
заданной
-
матрице активного четырехполюсника
(табл. 12.1) постройте его Т- образную схему
замещения.
Таблица 12.1
Исходные данные к задаче 12.1
Вариант |
|
|
|
|
1 |
6,5 |
450 |
8,5 |
7 |
2 |
5 |
20 |
8 |
6 |
3 |
2 |
1 |
5 |
5 |
4 |
1 |
1 |
5 |
2 |
5 |
8 |
1 |
2 |
4 |
6 |
6 |
1 |
4 |
8 |
7 |
8 |
1 |
2 |
8 |
8 |
10 |
1 |
4 |
5 |
9 |
10 |
2 |
6 |
6 |
10 |
8 |
1 |
4 |
4 |
11 |
10 |
1 |
5 |
4 |
12 |
10 |
2 |
4 |
8 |
13 |
6 |
2,5 |
8 |
4 |
14 |
9 |
2 |
8 |
6 |
15 |
9 |
1 |
6 |
6 |
16 |
10 |
1 |
8 |
7 |
17 |
8 |
1 |
6 |
6 |
18 |
16 |
3 |
4 |
8 |
19 |
14 |
3 |
5 |
9 |
20 |
15 |
4 |
5 |
9 |
21 |
16 |
3 |
4 |
6 |
22 |
15 |
3 |
6 |
8 |
23 |
16 |
3 |
8 |
10 |
24 |
16 |
3 |
6 |
8 |
25 |
8 |
4 |
6 |
6 |
26 |
10 |
2 |
6 |
6 |
27 |
12 |
1 |
8 |
9 |
28 |
10 |
10 |
8 |
9 |
29 |
12 |
10 |
8 |
10 |
30 |
10 |
10 |
8 |
10 |
,
Ом-1
,
Ом-1
,
Ом-1
,
Ом-1
З а д а ч а 12. 2
Преобразуйте Т-образную схему замещения, полученную в задаче 12.1, в П- образную.
З а д а ч а 12. 3
По данным табл. 12.2. постройте схему замещения четырехполюсника, используя его Н- параметры.
З а д а ч а 12. 4
Определите
коэффициент передачи четырехполюсника
,
описанного Н
-
параметрами, приведенными в табл. 12.2,
если он нагружен на сопротивление
.
З а д а ч а 12. 5
Для
усилительного каскада (рис. 12.2), транзистор
которого описан в табл. 12.2 Н
- параметрами,
определить коэффициент усиления
,
при значениях
и
,
приведенных в той же таблице.
Рис. 12.2. Схема усилительного каскада с общим эмиттером
З а д а ч а 12. 6
Для цепи, представленной на схеме рис. 12.3, вычислите коэффициент усиления по напряжению по данным табл.12.3.
Рис. 12.3. Схема к задаче 12.6
Методические указания: анализ начните с разбиения цепи на простые активные и пассивные четырехполюсники. Описав элементарные четырехполюсники в соответствующей системе параметров, замените схему одним четырехполюсником, при этом выберите вариант, требующий наименьших вычислений.
Таблица 12.2
Исходные данные к задачам 12.3, 12.4, 12.5
Вариант |
|
|
|
|
Ом |
Ом |
Ом |
1 |
330 |
16 |
56 |
62,5 |
1 |
3 |
1 |
2 |
650 |
32 |
40 |
15 |
2 |
6 |
2 |
3 |
700 |
30 |
40 |
2 |
3 |
7 |
3 |
4 |
800 |
40 |
30 |
15 |
4 |
8 |
4 |
5 |
600 |
35 |
25 |
2 |
6 |
6 |
5 |
6 |
650 |
30 |
35 |
25 |
6,5 |
6,5 |
6 |
7 |
600 |
0 |
30 |
5 |
6 |
6 |
7 |
8 |
300 |
16 |
50 |
5 |
5 |
3 |
8 |
9 |
350 |
15 |
45 |
6 |
4 |
3,5 |
9 |
10 |
450 |
15 |
45 |
7 |
4,5 |
4,5 |
1 |
11 |
550 |
20 |
50 |
7 |
5,5 |
5,5 |
2 |
12 |
650 |
25 |
40 |
8 |
6,5 |
6,5 |
3 |
13 |
350 |
15 |
50 |
6 |
3,5 |
3,5 |
4 |
14 |
330 |
15 |
60 |
7 |
3,3 |
3,3 |
5 |
15 |
340 |
16 |
70 |
8 |
3,4 |
3,4 |
6 |
16 |
100 |
1 |
30 |
10 |
1 |
1 |
7 |
17 |
1100 |
1 |
75 |
9 |
11 |
1 |
2 |
18 |
1300 |
0,5 |
90 |
12 |
13 |
1,3 |
1 |
19 |
200 |
1 |
70 |
50 |
2 |
0,2 |
1 |
20 |
1300 |
0,5 |
90 |
12,5 |
1,3 |
1,3 |
2 |
21 |
1300 |
0,2 |
110 |
10,5 |
1,3 |
1,3 |
3 |
22 |
1000 |
0,5 |
50 |
5 |
1 |
1 |
3 |
23 |
600 |
32 |
20 |
15 |
6 |
0,6 |
4 |
24 |
550 |
30 |
25 |
20 |
5,5 |
0,55 |
5 |
25 |
450 |
35 |
25 |
25 |
4,5 |
0,45 |
6 |
26 |
650 |
30 |
35 |
20 |
6,5 |
0,65 |
5 |
27 |
600 |
25 |
25 |
15 |
6,1 |
0,6 |
6 |
28 |
300 |
30 |
50 |
6,5 |
3 |
0,3 |
2 |
29 |
250 |
2 |
60 |
50 |
2,5 |
0,25 |
2 |
30 |
350 |
2,5 |
50 |
50 |
3,5 |
0,35 |
1 |
,
,
,
Таблица 12.3
Исходные данные к задачам 12.6, 12.7
Вариант |
, кОм |
кОм |
, кОм |
, кОм |
Ом |
Ом |
Ом |
|
1 |
5,0 |
2,5 |
1 |
3 |
25 |
100 |
1,0 |
0,98 |
2 |
4,8 |
2,4 |
1,1 |
3,1 |
30 |
120 |
1,1 |
0,95 |
3 |
4,6 |
2,3 |
1,0 |
3,2 |
35 |
150 |
1,2 |
0,98 |
4 |
4,4 |
2,25 |
1,2 |
3,3 |
40 |
200 |
1,3 |
0,99 |
5 |
4,6 |
2,35 |
1,0 |
3,4 |
45 |
250 |
1,4 |
0,98 |
6 |
4,5 |
2,45 |
1,2 |
3,5 |
50 |
200 |
1,5 |
0,95 |
7 |
4,7 |
2,05 |
1,4 |
3,6 |
55 |
220 |
1,6 |
0,96 |
8 |
4,8 |
2,1 |
1,5 |
3,7 |
60 |
240 |
1,7 |
0,92 |
9 |
4,9 |
2,2 |
1,4 |
3,8 |
55 |
260 |
1,8 |
0,93 |
10 |
5,0 |
2,3 |
1,45 |
3,9 |
50 |
220 |
1,9 |
0,94 |
11 |
5,1 |
2,4 |
1,4 |
4,0 |
45 |
200 |
2,0 |
0,95 |
12 |
5,1 |
2,5 |
1,35 |
4,2 |
40 |
180 |
2,1 |
0,96 |
13 |
5,4 |
2,6 |
1,45 |
4,5 |
35 |
160 |
2,2 |
0,97 |
14 |
5,0 |
2,7 |
1,5 |
4,2 |
30 |
140 |
2,3 |
0,98 |
15 |
5,2 |
2,8 |
1,6 |
4,5 |
25 |
120 |
2,4 |
0,92 |
16 |
5,0 |
2,7 |
1,0 |
3 |
30 |
100 |
1.0 |
0,95 |
17 |
4,9 |
2,6 |
1,1 |
3,1 |
20 |
120 |
1,2 |
0,94 |
18 |
4,8 |
2,5 |
1,2 |
3,2 |
40 |
140 |
1,3 |
0,93 |
19 |
4,9 |
2,4 |
1,3 |
3,3 |
50 |
150 |
1,4 |
0,92 |
20 |
5,0 |
2,3 |
1,4 |
3,4 |
60 |
160 |
1,5 |
0,98 |
21 |
5,1 |
2,2 |
1,3 |
3,5 |
50 |
180 |
1,6 |
0,97 |
22 |
5,2 |
2,1 |
1,35 |
3,6 |
55 |
200 |
1,7 |
0,96 |
23 |
5,3 |
2,0 |
1,4 |
3,5 |
45 |
200 |
1,8 |
0,95 |
24 |
5,35 |
2,1 |
1,45 |
3,4 |
35 |
220 |
1,9 |
0,99 |
25 |
5,3 |
2,2 |
1,46 |
3,5 |
25 |
300 |
2,0 |
0,98 |
26 |
5,25 |
2,3 |
1,5 |
3,4 |
55 |
250 |
2,1 |
0,97 |
27 |
5,0 |
2,4 |
1,55 |
3,3 |
60 |
200 |
2,2 |
0,95 |
28 |
5,1 |
2,5 |
1,45 |
3,4 |
65 |
150 |
2,3 |
0,98 |
29 |
5,2 |
2,6 |
1,5 |
3,2 |
50 |
100 |
2,4 |
0,94 |
30 |
5,0 |
2,5 |
1,4 |
3,0 |
55 |
120 |
2,0 |
0,93 |
,
,
,
,
З а д а ч а 12. 7
Для цепи, представленной на схеме рис. 12.4, определите - параметры четырехполюсника, если физические параметры транзистора приведены в табл. 12.3.
Рис. 12.4. Схема к задаче 12.7