Применяя формулу (1), получим
Следовательно,
4)
Площадь грани А1
А2
А3
равна половине площади параллелограмма,
построенного на векторах
и
.
Обозначим через вектор
векторное
произведение векторов
и
,
тогда площадь параллелограмма
,
а площадь грани
Координаты
вектора
найдем по формуле (3):
(11;
2; 10)
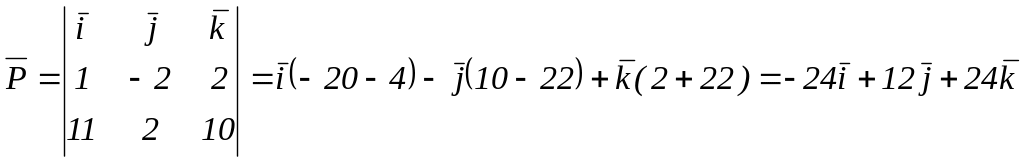
кв.
ед.
5)
Объем пирамиды V
в шесть раз меньше объема параллелепипеда
V1,
построенного на трех некомпланарных
векторах, и равен абсолютной величине
их смешанного произведения. Вычислим
смешанное произведение
:
Следовательно, V1 параллелепипеда равен 144 куб. ед., а объем заданной пирамиды V = 144/6 =24 куб. ед.
6) Уравнение прямой, проходящей через две заданные точки А1(х1, y1, z1) и А2(х2, y2, z2) имеет вид
(7)
Подставив в (7) координаты точек А1 и А2, получим
7) Уравнение плоскости А1А2А3 – это уравнение грани А1А2А3, которое найдено в п.3:
А1А2А3 : 2х – у – 2z – 3 = 0
8) Уравнение высоты, опущенной из вершины А4 на грань А1А2А3 – это перпендикуляр А4Д. Каноническое уравнение прямой в пространстве имеет вид
(8)
где х0, у0, z0 – координаты точки, через которую проходит прямая (8), а m, n, p – направляющие коэффициенты этой прямой. По условию прямая проходит через точку А4(0; 1; 4) и перпендикулярные грани А!А2А3 для которой (2; -1; -2), т.е. подставив эти данные в формулу (8), получаем
-
уравнение высоты А4Д
Пример 3. Данную систему уравнений:
решить по формулам Крамера (через определитель) и средствами матричного исчисления (с помощью обратной матрицы).
Решение.
Обозначим через А матрицу коэффициентов при неизвестных;
Х – матрицу - столбец неизвестных х1, х2, х3;
В – матрицу – столбец свободных членов:
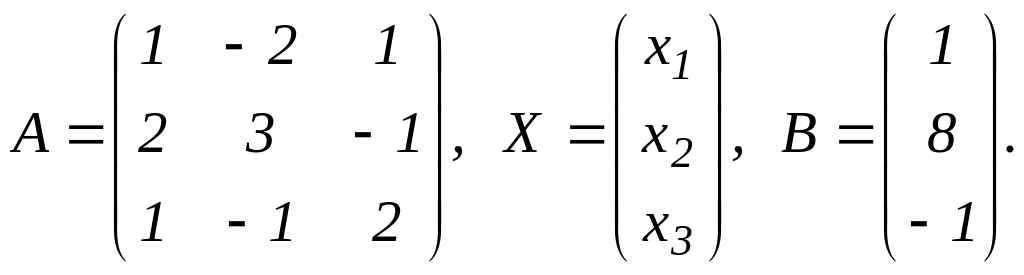
С учетом этих обозначений данная система уравнений примет следующую матричную форму:
(1)
Если
матрица А
–
невырожденная
(ее определитель
),
то она имеет обратную матрицу А-1.
умножив обе части уравнения (1) на А-1
,
получим:
,
но
-
единичная матрица, а ЕХ
= Х,
поэтому
(2)
Равенство (2) называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо выписать обратную матрицу А-1.
Пусть
имеем невырожденную матрицу
и ее определитель равен Δ, тогда
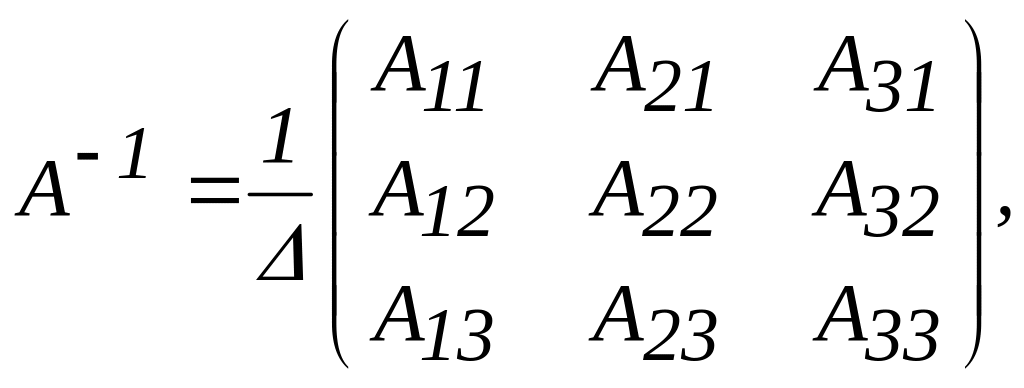где Aij
(i
= 1,2,3; j
= 1,2,3) – алгебраическое
дополнение элемента aij
в определителе матрицы А
и
где Mij – минор (определитель) второго порядка, полученный вычеркиванием i –й строки и j – го столбца в определителе матрицы А.
Вычислим определитель Δ и алгебраические дополнения Aij элементов матрицы А.
следовательно
матрица А
невырожденная
и имеет обратную матрицу А-1.
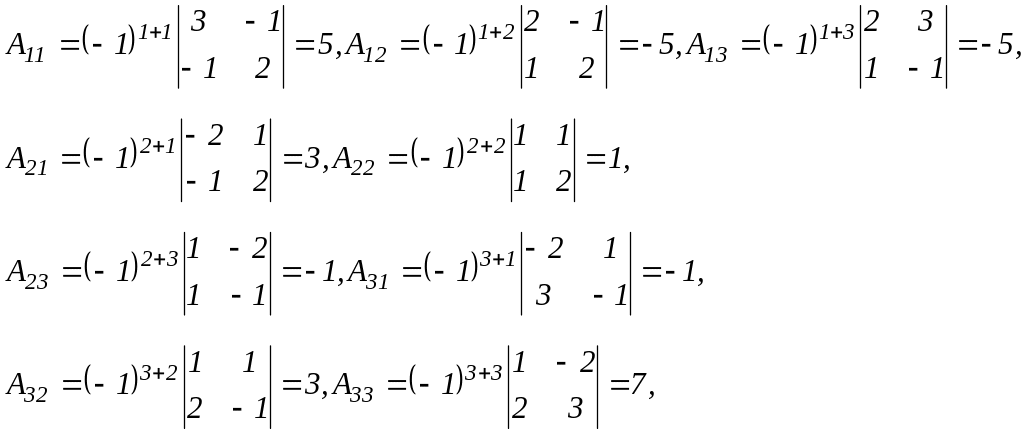
тогда
По формуле (2) находим решение данной системы уравнений в матричной форме:
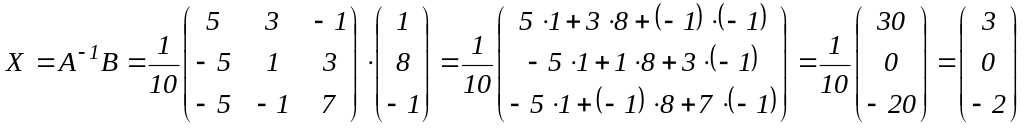
отсюда х1=3, х2=0, х3=-2.