Книги и методы для курсовых / Kody_i_ustroystva_pomehoust__kodir

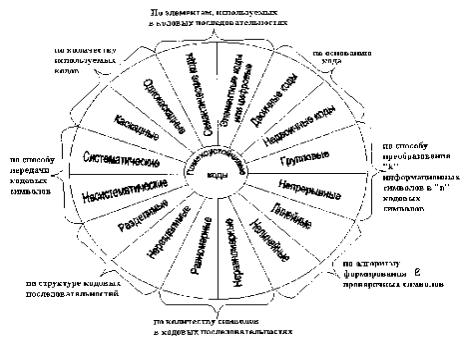
основанием кода (q), кодовым расстоянием (d0), избыточностью (r), структурой, функциональным назначением, алгоритмами декодирования, способом передачи кодовых символов и т.д.

Для лучшего понимания и практического использования помехоустойчивых кодов вводят классификацию кодов, по характерным признакам их отличия. Наиболее широко используется следующая структура классификации (рис.1.5).

1. По форме представления передаваемой информации —

помехоустойчивый код можно разделить на две группы или на два способа представления информации, а именно: семантические коды и элементные (цифровые, дискретные) коды.

Семантические коды - используют короткие комбинации букв, обозначающие целые фразы, например, SOS - сигнал опасности, ТТТ - сигнал безопасности и т.д., а также сюда входят, так называемые Z-коды и Q-коды, которые находят применение в радиосвязи, например, ZSU - ваши сигналы неразборчивы, QKM - мне мешают на этой волне и т.д.

Рис.1.5. Структурная схема классификации помехоустойчивых кодов

Элементные (дискретные) коды - характеризуются тем, что каждому символу источника присваивается определенное число в заданной системе счисления и которое отображается соответствующей кодовой последовательностью, например, 10, 00 или 100, 000, 010 и т.д. Здесь элемент "1" и "0";

2. По основанию кода или по количеству единичных элементов, используемых для формирования кодовой последовательности, коды делятся на двоичные (т.е. q=2, GF(q)=GF(2)) и недвоичные, когда q>2; GF(2m,m³2 и q=l;0;

3. По способу преобразования "k" информационных символов в "n"

кодовых символов делятся нa блоковые и непрерывные. В блоковых кодах из "k" информационных символов формируется "l" проверочных символов и "l" проверочных символов совместно c "k" информационными символами образуют кодовую последовательность из n=(k+1) кодовых символов (информационные символы каждого входного блока не оказывают влияния на формирование проверочных символов предшествующей кодовой последовательности и последующих кодовых последовательностей).

В непрерывных кодах каждый информационный символ может оказывать влияние на формирование проверочных символов в течение "m" тактов, где "m" - количество ячеек памяти регистра сдвига (RG) кодера. В данных кодах нет четкого деления на кодовые последовательности из "n" кодовых символов;

4.По алгоритму формирования (l) проверочных символов – на линейные

инелинейные. В линейных кодах проверочные символы формируются путем суммирования по модулю два информационных символов, стоящих на определенных позициях. В нелинейных кодах проверочные символы формируются путем суммирования информационных символов по модулю отличному от два;

5.По количеству символов в кодовых последовательностях – на равномерные и неравномерные коды. В равномерных кодах все кодовые последовательности помехоустойчивого кода имеют одинаковую длину, т.е. "n"=const. У неравномерных кодов один и тот же помехоустойчивый код может

иметь кодовые последовательности с разной длиной, т.е. "n"¹const;

6.По структуре кодовых последовательностей – на разделимые и неразделимые. К разделимым кодам относятся такие помехоустойчивые коды у которых есть четкое деление на блоки из "k" информационных символов, l - проверочных символов и на кодовые последовательности из "n" символов; такое деление справедливо для всех кодовых последовательностей. К неразделимым кодам относятся такие коды у которых нет четкого деления на информационные, проверочные блоки и на кодовые последовательности;

7.По способу передачи кодовых символов – на систематические и несистематические. В систематических кодах в канал связи первоначально передается информационные символы (блок из "k" информационных символов), а затем блок из "l" проверочных символов. В систематических кодах сохраняются статистические связи между "k" информационными символами данной кодовой последовательности. В несистематических кодах нет четкого деления на блоки информационных символов и проверочных и, следовательно, нет статистической связи между информационными символами и в канал связи кодовые символы передаются по "псевдослучайному закону", т.е. может передан(ы) проверочный(е) символ(ы), например, два проверочных символа, а затем переданы три информационных символа, а затем один проверочный, два - информационных и т.д. Примером несистематических кодов являются коды Плоткина и коды с постоянным весом (с равным количеством логических "1").

К систематическим кодам, в первую очередь, относятся двоичные равномерные групповые линейные коды БЧХ, Файра, РС-коды, СК и др., которые

вдальнейшем будем рассматривать. Систематические помехоустойчивые коды, у которых искажение одной кодовой последовательности ведет к искажению других кодовых последовательностей носят название статистических систематических помехоустойчивых кодов без синхронизации, а в противном случае называются статистическими систематическими помехоустойчивыми

кодами с самосинхронизацией;

реализующих, большое число кодов и т.д. Недостаток - сравнительно низкая корректирующая способность многих кодов.

Арифметические способы и алгоритмы де/кодирования реализуются на основе использования теории чисел и множеств, полученных путем суммирования их по модулю некоторого "выбранного" числа. Наибольшее применение данные коды получили в ЭВМ.

Геометрические способы и алгоритмы де/кодирования реализуются на основе использования теории n-мерного пространства и проективной геометрии (коды Элайса, коды Мешковского и др.). Отличительная черта этих кодов - высокая сложность их реализации, малое число помехоустойчивых кодов; имеют ограниченное применение на практике.

Эвристические способы и алгоритмы де/кодирования базируются на основе использования определенных умозрительных логических рассуждений (коды с постоянным весом и др.). Ввиду невысокой корректирующей способности данные коды находят ограниченное применение.

Неалгебраические алгоритмы декодирования используют в основном вероятностные алгоритмы декодирования, т.е. когда при декодировании используется информация как о его полярности, так и надежности его принятия. Данные алгоритмы обеспечивают более высокие корректирующие способности, но и имеют более высокую сложность реализации кодов.

Контрольные вопросы и задачи

1.Пояснить сущность помехоустойчивого кода и способа помехоустойчивого кодирования.

2.Перечислить возможные области применения кодов и шифров.

3.При каких условиях возможно только: обнаружение ошибок; обнаружение

икоррекция ошибок.

4.Определить кратность корректируемых и обнаруживаемых ошибок блоковым кодом с параметрами (n, k)=(16,9).

5.Назвать и пояснить сущность основных характеристик (параметров) помехоустойчивых кодов.

6.Дать определение кодовому и минимальному кодовому расстоянию. Определить d0, если заданы следующие четыре кодовые последовательности: F1(x)=100110, F2(x)=010101, F3(x)=001011 и F4(x)=111111.

7.Назвать основные признаки классификации помехоустойчивых кодов.

8.Определить d0 , если помехоустойчивый код используется для коррекции трехкратных ошибок.

9.Для кодовых последовательностей пункта 6 при k=3 определить: n, l, d0 wi.

10.Доказать, что для одновременного исправления tисп. ошибок и

обнаружения tобн. ошибок необходимо и достаточно, чтобы d0 ³ tисп. + tобн. + 1.

2.ГРУППОВЫЕ БЛОКОВЫЕ КОДЫ

2.1.Определение групповых кодов, основные свойства и классификация кодов

Большинство известных ”хороших” помехоустойчивых кодов (коды с высокой корректирующей способностью, с малой избыточностью и с простыми алгоритмами декодирования) принадлежат к классам групповых линейных блоковых кодов. Теория и практика построения данных кодов разработана достаточно подробно. В чём же сущность групповых кодов? Групповые коды–это такие линейные блоковые коды, совокупность кодовых слов которых вместе с нулевым кодовым словом, снабженное операцией посимвольного (поразрядного) сложения по модулю два, образуют математическую структуру, называемую группой и соответствуют основным свойствам групп.

В соответствии с [3…5] группой G называется множество элементов с определённой для каждой пары элементов операцией (обозначаемой знаком *), обладающее следующими четырьмя свойствами:

1)замкнутость: для каждой пары “a” и “b” из множества элемент с=а*b принадлежит множеству;

2)ассоциативность: для всех “а”, “b” и “с” из множества а*(b*с)=(а*b)*с;

3)существование единицы: в множестве существует элемент ”е“, называемый единичным элементом и такой, что а*е=е*а=а для любого элемента “а” множества;

4)существование обратных элементов: для любого “a” из множества существует некоторый элемент “b” из множества, называемый обратным элементу “a” и такой, что

a*b=b*a=e .

Если группа G содержит конечное число элементов, то она называется конечной группой, а число элементов в G называется порядком G.

Некоторые группы обладают тем дополнительным свойством, что для любых “a” и “b” из группы a*b=b*а. Это свойство называется коммутативностью.

Группы, обладающие этим дополнительным свойством, называются коммутативными или абелевыми группыми. Далее рассматриваются помехоустойчивые коды, которые соответствуют свойствам абелевых групп.

В случае абелевых групп групповая операция обозначается знаком или символом “+” и называется сложением (даже тогда, когда она не является обычным арифметическим сложением). В этом случае единичный элемент называется нулем, и обозначается “0”, а обратный элементу “а” элемент записывается в виде “–а”, так что

а+(-а)=(-а)+а=0.

Иногда групповая операция обозначается символом “*” и называется умножением (даже тогда, когда она не является обычным арифметическим умножением). В этом случае единичный элемент называется единицей и обозначается “1”, а обратный элементу “а” элемент записывается в виде “а−1 ”, так что а*а −1 = а−1 *а=1.

Если N есть группа, а M есть некоторое подмножество в N, тогда M называется подгруппой группы N, если оно является группой относительно ограничения операции * на M. Таким образом, подгруппа есть некоторое множество элементов группы, если оно удовлетворяет всем аксиомам группы. Наиболее простыми являются так называемые циклические подгруппы, которыми обладает любая группа N. Число элементов в группе определяет порядок группы. Если же все элементы группы могут быть представлены как степень одного элемента, то такая группа называется циклической.

Разработано большое количество классов групповых линейных блоковых кодов. На рис.2.1 приведена структурная схема с классификацией данных кодов. За основу классификации принят принцип их построения.

Далее рассмотрим принципы построения и реализации групповых блоковых кодов, которые находят широкое применение на практике.

Далее рассматриваются только двоичные разделимые систематические линейные блоковые коды, основными свойствами которых являются [1…5]:

-линейность кода: линейность кода определяется специально выбираемой структурой кода. Линейность кода существенно упрощает процедуру кодирования и декодирования, позволяя выразить каждую кодовую последовательность в виде “линейной” комбинации небольшого числа выделенных кодовых последовательностей, так называемых базисных векторов;

-сумма по модулю два двух кодовых последовательностей также является кодовой последовательностью;

-линейный блоковый код всегда содержит кодовую последовательность, состоящую целиком из нулей;

-если сложить по модулю два некоторую кодовую последовательность со всеми кодовыми последовательностями, то снова получится множество всех кодовых последовательностей, расположенных, быть может, в другом порядке;

-вес кодовой последовательности (vкп ) всегда должен быть ≥ d0 ;

-вес проверочной части кодовой последовательности ( vпр,кп ) должен быть всегда ≥ (d0 -1);

-вес суммы по модулю два двух разрешенных кодовых последовательностей

(v åкп ) должен быть всегда ≥ (d0 -1), но допускается ≥( d0 -2);

- групповой двоичный линейный блоковый код полностью задается как порождающей G k,n (x), так и проверочной H l,n (x) матрицами.

В соответствии с [1…3] наименьшую сложность построения и реализации имеют разделимые систематические двоичные линейные блоковые коды. При использовании данных кодов для повышения достоверности ПИ с выхода источника информации передаваемая информация поступает в виде информационных блоков, содержащих “k” двоичных символов (дв.сим.). Данные информационные блоки назовем сообщениями и обозначим через Q(x). Данные сообщения являются безызбыточными и составляют Kp=2 k разрешенных кодовых сообщений. В кодере из поступивших “k” информационных символов