только он. Очевидно, что непротиворечивость выбора на основе только левого контекста обеспечить сложнее, чем на основе левого и правого контекстов. Поэтому класс LR(0) грамматик уже, чем класс LR(1) грамматик, для которых учитывается и правый контекст тоже.

Ситуация представляет собой множество правил КС-грамматики, в которых указывается положение считывающей головки МП-автомата, которое может возникнуть при разборе сентенциальной формы этой грамматики. Это положение обозначается в правой части правила специальным символом •. Этот символ не входит в алфавит грамматики. Если S – аксиома некоторой Для КС-грамматики G(T, N, P, S), где S→α1 | α2 | … | αn P, αi V*, начальной ситуацией будет множество правил R={S→•α1 , S→•α2 , … , S→•αn }. Последовательность ситуаций строится по следующим правилам:

1.r R : A→γ•Bβ, A,B N, γ,β V* , p P : B→α, α V* R=R {B→•α}, т.е. ситуация пополняется новыми пра-

вилами

2.r R : A→γ•xβ, A N, γ,β V* , x V R’={A→γx•β }, и R→xR’ т.е. строится новая ситуация, знак →x означает, что новая ситуация следует из текущей по символу x.

Множество связанных между собой по разным символам ситуаций и является последовательностью ситуаций. Она может быть изображена в виде графа. Поскольку количество правил грамматики конечно, то и последовательность ситуаций тоже конечна. Для построения управляющего автомата все ситуации в последовательности нумеруются: R0, R1, R2, …, Rn. Здесь R0

– начальная ситуация. Пример:

G=({a,b},{S}, {S→aSS | b},S). Построим последовательность ситуаций.

Вначале строим пополненную грамматику, поскольку аксиома встречается в правой части правил: G’=({a,b},{S,S’}, {S’→S, S→aSS | b},S’).

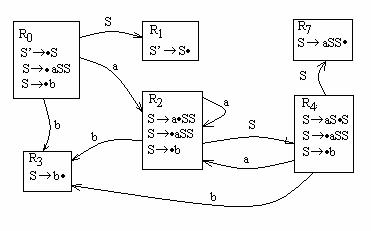
Итого получилось 6 ситуаций: 0,1,2,3,4,7. Граф:

Построение распознавателя. Распознаватель для LR(0) грамматики функционирует на основе управляющей таблицы. Она строится следующим образом: строками являются все ситуации грамматики, столбцы содержат все символы словаря (как терминальные так и нетерминальные и маркер конца строки). Элементом ij таблицы является операция, которую будет выполнять автомат, если он находится в состоянии i, а текущим символом является j. Автомат использует 2 стека – стек символов и стек состояний. Возможны 4 типа операции:

-перенос(сдвиг) П(s). Текущий символ помещается в стек символов. Если это терминал – перемещение головки чтения. Символ входной строки фиксируется в качестве текущего. В стек состояний заносится s. Автомат переходит в состояние s.

-свертка С(n, A, k). Свертка по правилу k: A→α. Из вершин обоих стеков удаляется по n символов, где n = |α|. Нетерминал А фиксируется в качестве текущего символа. Номер правила (k) заносится в разбор грамматики. Переход в состояние, указанное на вершине стека состояний.

-Ошибка E. Разбор не может быть продолжен. Строка отвергается.

-Конец. Разбор окончен, строка принята.

Управляющая таблица U = {uij } строится на основе последовательности ситуаций.

1.Для каждой ситуации Ri создается строка таблицы i.

2.Для каждой ситуации Ri выполняется следующее:

-r Ri : A→γ•, γ V* , A N, k – номер правила A→γ uij = П (|γ|, A, k), для всех j≠S

-r Ri : A→γ•xβ, γ,β V* , x V, A N, Ri→x Rj uix = С (j)

3.u0S = Конец

4.Во все оставшиеся пустыми ячейки таблицы заносится Ошибка. При этом каждой ячейке можно поставить в соответствие

свое диагностическое сообщение, локализующее и классифицирующее ошибку.

Если таблицу удалось заполнить непротиворечивым образом, т.е. для одной и той же ячейки таблицы нет взаимоисключающих действий, то рассматриваемая грамматика является LR(0) грамматикой. Перед началом работы распознаватель устанавливается в состояние 0, головка чтения – на первый символ входной строки, который принимается в качестве текущего. Стек символов содержит #, стек состояний 0. Дальнейшее функционирование происходит на основе таблицы. Пример:

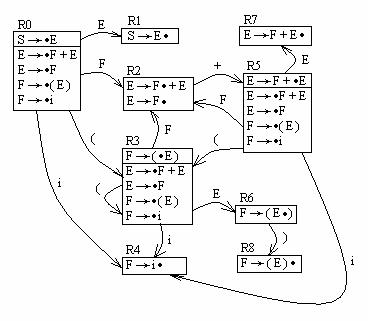
Итого получилось 8 ситуаций. Граф:

В позиции (2,+) возник конфликт перенос-свертка. Соответственно данная грамматика не является LR(0). Рассмотрим построение распознавателя для LR(1) грамматик.

Ситуация для LR(1) грамматики задается несколько сложнее. Если S – аксиома некоторой Для КС-грамматики G(T, N, P, S), где S→α1 | α2 | … | αn P, αi V*, начальной ситуацией будет множество правил R={S→•α1 /#, S→•α2 /#, … , S→•αn

/#}. Таким образом, в правилах ситуаций указывается еще и правый контекст. Последовательность ситуаций строится по следующим правилам:

1.r R : A→γ•Bbβ /a, A,B N, a,b T, γ,β V* , p P : B→α, α V* R=R {B→•α /b}, т.е. ситуация пополняется новыми правилами с учетом правого контекста

2.r R : A→γ•B /a, A,B N, a T, γ V* , p P : B→α, α V* R=R {B→•α /a}

3.r R : A→γ•BCβ /a, A,B,C N, a T, γ,β V* , p P : B→α, α V* , c S(C) R=R {B→•α /c}, где S(C) – Мно-

жество символов предшественников

4.r R : A→γ•xβ /a, A N, γ,β V* , a T, x V R’={A→γx•β /a}, и R→xR’

Пример: G({+, (, ), i},{S, E, F},{S→E; E→F+E; E→F; F→(E); F→i}, S)

0. R0={ S→•E /#}

1. Поскольку существуют правила для E, то R0= R0 { E→•F+E /# , E→•F /#} R0={ S→•E /#, E→•F+E /# , E→•F /#} 1. Поскольку существуют правила для F, то R0= R0 { F→•(E) /+ , F→•i /+, F→•(E) /# , F→•i /# }

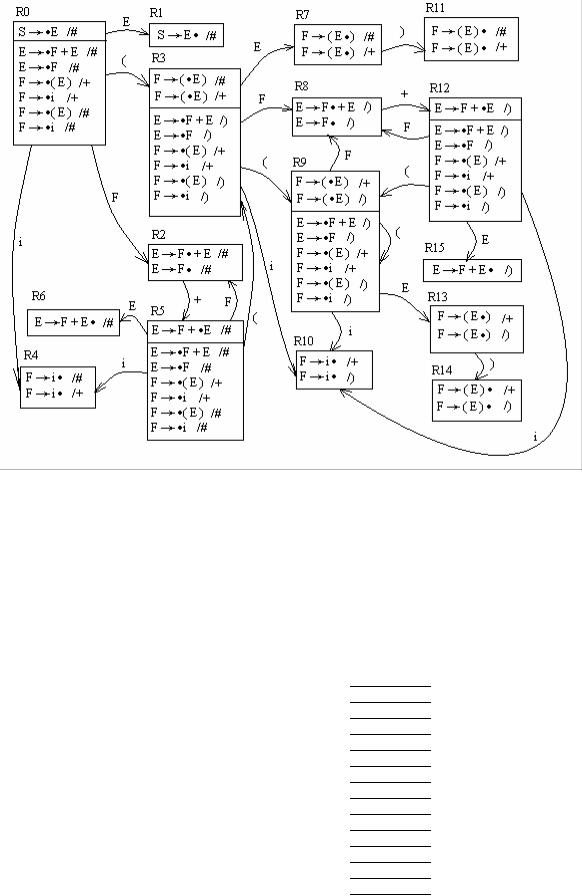
Продолжая построения аналогичным образом, получим 15 ситуаций. Граф:

Построение распознавателя для LR(1) грамматики. Распознаватель для LR(1) грамматики строится по похожим принципам, что и для LR(0). Управляющая таблица U = {uij } строится следующим образом.

1.Для каждой ситуации Ri создается строка таблицы i.

2.Для каждой ситуации Ri выполняется следующее:

-r Ri : A→γ• /a, γ V* , A N, a T, k – номер правила A→γ uia = П(|γ|, A, k)

-r Ri : A→γ•xβ /a, γ,β V* , x V, A N, a T, Ri→x Rj uix = С(j)

2.u0S = Конец

3.Во все оставшиеся пустыми ячейки таблицы заносится Ошибка.

Если таблицу удалось заполнить непротиворечивым образом, то рассматриваемая грамматика является LR(1) грамматикой. Перед началом работы распознаватель устанавливается в состояние 0, головка чтения – на первый символ входной строки, который принимается в качестве текущего. Стек символов содержит #, стек состояний 0. Дальнейшее функционирование происходит на основе таблицы. Пример:

Как видно из примера, число состояний значительно увеличилось, более того, число элементов в каждой ситуации тоже больше, чем для LR(0) грамматики. Посмотрим, как происходит разбор строки (i)+i:

Конфликт при построении LR(0) распознавателя в одной-единственной ячейке привел к необходимости построения LR(1) грамматики, для которой и ситуации строятся значительно сложнее и число состояний значительно возрастает. Поиск методов упрощения построения распознавателей при подобных конфликтах привел к появлению SLR(1) (от simple - простая) и LALR(1) (от look ahead – заглядывание вперед) грамматик. Если проанализировать конфликтную позицию (2,+) {С(1,Е,3), П(5)} таблицы LR(0) распознавателя, то видно, что свертка должна производиться только при последующем символе #, т.е. конфликт разрешается в пользу переноса. Грамматики, для которых подобный анализ позволяет устранить конфликты, относятся к классу SLR(1) грамматик. LALR(1) грамматики используют более сложный анализ контекста.

Формально ситуации для SLR(1) грамматик строятся так же, как и для LR(0) грамматик, но управляющая таблица заполняется иначе:

Управляющая таблица U = {uij } строится на основе последовательности ситуаций.

Если таблицу удалось заполнить непротиворечивым образом, то рассматриваемая грамматика является SLR(1) грамматикой. Перед началом работы распознаватель устанавливается в состояние 0, головка чтения – на первый символ входной строки, который принимается в качестве текущего. Стек символов содержит #, стек состояний 0. Дальнейшее функционирование происходит на основе таблицы. Пример:

Пример. Возьмем имеющуюся конфликтную последовательность ситуаций. Сначала построим множество символов – последователей для каждого из нетерминалов: F(S)={#}; F(E)={),#}; F(F)={+,),#}.

Заполним управляющую таблицу:

Как видим, разбор строки идентичен распознавателю LR(1) с точностью до номера состояния.

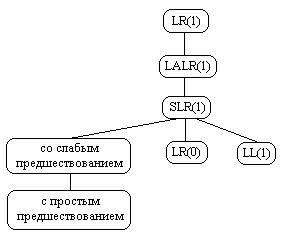
Рассмотрим иерархию КС-грамматик:

Чем уже класс грамматик, тем более простой распознаватель будем иметь на выходе, и тем проще его синтез. С другой стороны, приведение грамматики к более узкому классу требует больших усилий. Иногда, если часть правил не описывается выбранным классом грамматик, они анализируются отдельно, по дополнительному алгоритму.

Любая SLR(1) грамматика является LR(1) грамматикой, но не

наоборот. Класс языков, задаваемый SLR(1) грамматикой уже, чем

для LR(1), а это значит, что не всякий детерминированный КСязык может быть задан SLR(1) грамматикой.

Любая SLR(1) грамматика является LALR(1) грамматикой, но не наоборот. Любой детерминированный КС-язык может быть задан LALR(1) грамматикой. Это значит, что классы языков, задаваемых LALR(1) и LR(1) грамматиками, совпадают, однако не всякая LR(1) грамматика является LALR(1) грамматикой.

С другой стороны, как правило, чем уже класс грамматик в этой иерархии, тем меньше возможностей по диагностированию

ошибок он предоставляет, при этом снижается точность локализации и классификации ошибок.

Автоматизация построения синтаксических анализаторов решается с помощью различных пакетов, например YACC (Yet Another Compiler Compiler). Язык описывается в форме, близкой к форме Бэкуса-Наура, результатом является текст программы синтаксического анализатора. YACC реализует восходящий распознаватель на основе LALR(1) грамматики.