Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«Челябинский государственный университет»

Миасский филиал

Кафедра прикладной математики

УТВЕРЖДАЮ

Заведующий кафедрой

прикладной математики

Б.М. Тюлькин

Курс лекций

учебной дисциплины

ОПД.Ф.03. «Теория вероятностей и математическая статистика»

Миасс 2009

Тема 1. Классическая модель вероятностей.

1. СТАТИСТИЧЕСКИЙ ПОДХОД К ОПИСАНИЮ

СЛУЧАЙНЫХ ЯВЛЕНИЙ

Теорией вероятностей называется наука о закономерностях массовых случайных явлений.

Испытание - комплекс определенных условий, воспроизводимый сколь угодно большое количество раз, наличие которого приводит к какому либо исходу. Исход случаен, если испытание, приводящее к какому-либо определенному исходу, имеет и другие исходы.

Среди всех возможных событий, которые в данном испытании могут произойти, можно выделить множество так называемых элементарных событий (или элементарных исходов) , выделяемых из множества всех событий по следующим признакам:

1) все они взаимно исключают друг друга, и в результате испытания обязательно происходит одно из этих событий;

2) каково бы ни было событие А, по наступившему элементарному событию можно судить о том, что наступило или не наступило событие А.

Точного определения элементарного события не существует.

Для простоты множество элементарных событий

будем считать конечным или счетным, т.е. дискретным.

Случайным событием (или просто событием) называется подмножество множества . Событие может состоять и из одного исхода, поэтому сами исходы также можно именовать событиями.

П р и м е р. Возьмем игральную кость (кубик, на гранях которого отмечены от одного до шести очков) и бросим его на стол. На верхней грани брошенного кубика выпадет какое-либо количество очков. Совокупность указанных условий (наличие у нас кубика, стола и процедура бросания кубика) - испытание. Количество очков, выпавших на верхней грани брошенного кубика, - исход этого испытания. Общее число случайных исходов равно шести. Случайным событием в данном примере будет, например, событие, состоящее в том, что на верхней грани окажется четное число очков. Это событие есть совокупность трех исходов: выпадения 2, 4 и 6 очков.

Множество элементарных событий состоит из шести элементарных событий А₁ , А₂ , ..., А₆ , заключающихся в том, что на верхней грани брошенной кости выпало 1, 2, ..., 6 очков соответственно.

Случайные события обозначают большими латинскими буквами А, В, С, ... или А₁ , А₂ , А₃ , ...

Достоверным событием называют событие, которое обязательно произойдет при данном испытании.

Невозможным событием называют событие, которое заведомо не произойдет при данном испытании.

События А₁ , А₂ , ..., А_n называются несовместными, если наступление одного из них исключает наступление других.

П р и м е р. Пусть в урне находятся три белых шара, пронумерованных цифрами 1, 2, 3, и два черных шара, пронумерованных цифрами 4, 5. Вынимаем наугад один из шаров. Пусть событие А состоит в том, что вытащенный шар - белый, а событие В состоит в том, что вынутый шар имеет четный номер. События А и В - совместные, так как из урны может быть вынут белый шар с номером 2. Далее, пусть событие С состоит в том, что вынут шар под номером 5. События А и С несовместны, так как белые шары пронумерованы цифрами 1, 2, 3.

События А₁ , А₂ , ..., А_n образуют полную группу событий, если в результате данного испытания обязательно произойдет одно из них. Совокупность А₁ , А₂ , ..., А_n может быть или конечной или счетной.

П р и м е р. Пусть в урне находятся три белых шара, пронумерованных цифрами 1, 2, 3, и два черных шара, пронумерованных цифрами 1, 2. Из урны наугад вынимают один шар. События:

А₁ - появление шара с цифрой 1,

А₂ - появление шара с цифрой 2,

А₃ - появление шара с цифрой 3 - образуют полную группу событий.

Полная группа событий А₁ , А₂ , ..., А_n называется полной группой несовместных событий, если в результате данного испытания обязательно произойдет одно и только одно событие данной группы.

П р и м е р. Брошена игральная кость. Пусть А₁ , А₂ , ..., А₆ - события, состоящие в том, что на верхней грани брошенной кости выпало 1, 2, …, 6 очков соответственно. События А₁ , А₂ , ..., А₆ образуют полную группу несовместных событий.

Случайное событие является множеством элементарных событий, которое является составом события.

П р и м е р. При социологическом опросе фиксируется возраст респондентов:

Х₁ = 50 лет,

Х₂ = 45 лет,

… ,

Х_n = 18 лет - элементарные события.

Откладывая эти значения на числовой оси, мы образуем множество элементарных событий, или пространство элементарных событий.

Рассмотрим возраст респондентов менее 50 лет, Х < 50.

Событие А = Х < 50 является составным событием, содержащим точки полуинтервала [0, 50).

Геометрической интерпретацией составного события является область пространства, образованная совокупностью точек - элементарных событий.

1.2 КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ

Частота события - отношение числа его появлений к числу всех произведенных опытов. Т. е. если при n опытах событие А появились m раз, то его частота в данной серии опытов равна m/n.

Факт рождения мальчика в конкретной семье является случайным событием, но в массовых случайных явлениях частота рождения мальчиков стабилизируется около некоторого значения. В середине XVIII века монах Зюсмильх увидел проявление "божественного" порядка в устойчивом соотношении чисел мальчиков и девочек среди новорожденных 21 : 20.

В классической модели теории вероятностей полагается, что:

1. Множество элементарных событий (исходов) одного испытания конечно и образует полную группу несовместных событий.

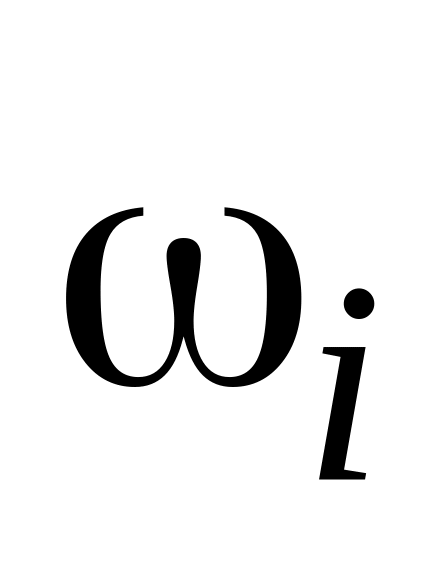2. С каждым элементарным исходом можно связать неотрицательное число 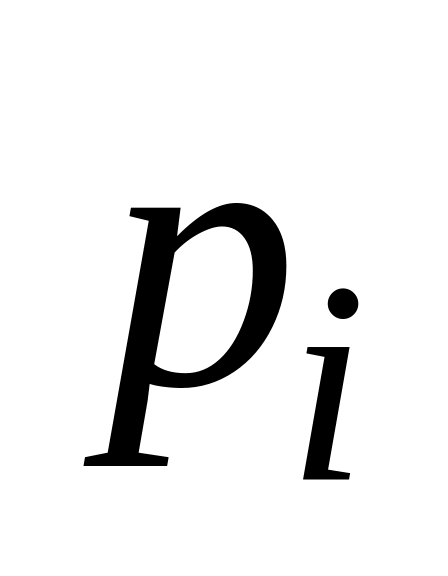, называемое вероятностью этого исхода, причем

.

3. Вероятность P(A) наступления события A, состоящего в том, что наступило одно из событий 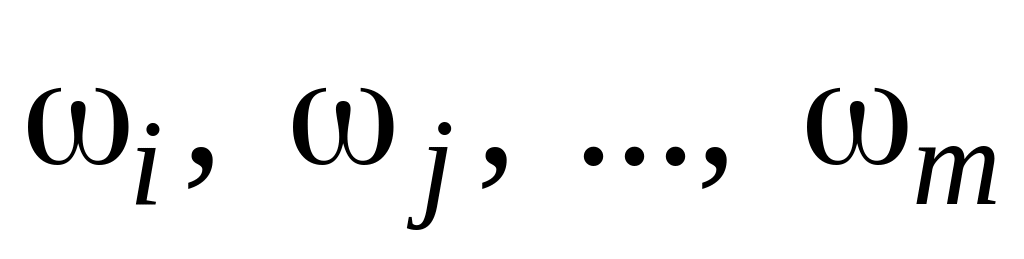, равна сумме вероятностей наступления этих событий

.

Здесь – события, благоприятствующие событию А.

4. В случае, когда события равновероятны, т. е. 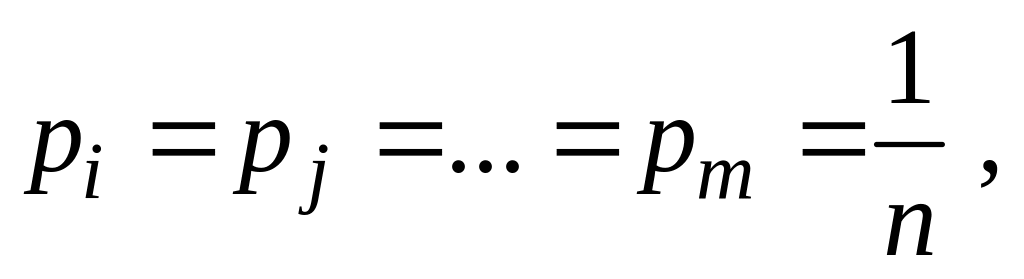вероятность P(A) вычисляется по формуле

P(A) = m/n,

( 1 )

где m - число исходов благоприятствующих событию A,

n - число всех равновозможных исходов.

1.3. Урновые схемы.

Комбинаторика  раздел математики о выборе и расположении элементов некоторого множества на основании каких-либо условий. Комбинаторика послужила основой классического подсчета вероятностей.

Выборкой объема k из совокупности n предметов называется любая последовательность предметов из этой совокупности длины k.

Теорема о комбинациях. Если предмет а можно выбрать m способами, а предмет b - n способами, то число всех упорядоченных пар вида (a, b) равно mn.

□ Пусть а₁ , а₂ , ..., а_m  все возможные способы выбора предмета а, b₁ , b₂ , ..., b_n  все возможные способы выбора предмета b.

Все пары можно разместить в таблицу размера так, чтобы пара (a_i , b_j) стояла на пресечении i-ой строки и j-го столбца, поэтому число таких пар равно числу клеток в таблице т.е. mn. ■^*

Выбранные предметы можно расположить в порядке их появления в последовательности  упорядоченная выборка.

Если не различать выборки, отличающиеся порядком следования предметов, то говорим о неупорядоченной выборке.

Схема извлечения шаров. Имеется урна с n шарами и пустой ящик с k нумерованными ячейками. Вынимаем из урны шар и кладем в 1-ю ячейку, затем вынимаем другой шар и кладем во 2-ю ячейку и т.д. до заполнения всех k ячеек.

Размещением из n предметов по k называется упорядоченная выборка k предметов из n возможных без возвращения.

Теорема о размещениях. Число упорядоченных размещений из n предметов по k равно

.

□ Первый предмет можно вынуть n способами. Т.к. он не возвращается, то 2-ой можно вынуть (n-1) способом и т.д., последний k-ый можно вынуть способом. Далее применяем теорему о комбинациях:

■ Перестановкой из n предметов называется размещение из n предметов по n.

Сочетанием из n предметов по k называется неупорядоченная выборка k предметов из n возможных без возвращения. (Имеется урна с n шарами, вынимаем из урны шар и бросаем в мешок. Повторяем, пока в мешке не наберется k шаров.)

Сочетание отличается от размещения тем, что в нем не учитывается порядок появления.

Теорема о сочетаниях. Число сочетаний из n предметов по k задается равенством

□ Набор из k извлеченных шаров можно упорядочить числом способов, равным числу перестановок P_k = k!, т.е. размещений в k! раз больше чем сочетаний. ■

Для числа сочетаний справедливо следующее равенство:

Это прямое следствие того факта, что каждому  элементному подмножеству однозначно соответствует  элементное подмножество X\Y множества X (табл. 1).

Таблица 1

n	k
	0	1	2	3	4	5	6	7	8	9	10
0	1
1	1	1
2	1	2	1
3	1	3	3	1
4	1	4	6	4	1
5	1	5	10	10	5	1
6	1	6	15	20	15	6	1
7	1	7	21	35	35	21	7	1
8	1	8	28	56	70	56	28	8	1
9	1	9	36	84	126	126	84	36	9	1
10	1	10	45	120	210	252	210	120	45	10	1

Размещениями с повторениями из n предметов по k называется упорядоченная выборка k предметов из n возможных с возвращением.

Теорема о размещениях. Число размещений с повторениями из n предметов по k задается равенством: .

□ 1-ый предмет можно вынуть n способами. Т.к. он возвращается в урну, то 2-ой также можно вынуть n способами и этот процесс повторяется k раз. Далее применяем теорему о комбинациях. ■

1.4. ФОРМУЛА ВЕРОЯТНОСТИ

Займемся подсчетом вероятностей. В урне имеется N шаров, из них K белых, (N-K) черных. Подсчитаем число всех возможных выборок объема n из N элементов. Общее число исходов равно . Выясним, сколько исходов из общего числа элементарных исходов благоприятствуют событию А  наличию в выборке объема n белых шаров в количестве k. Число способов, которыми можно из K белых шаров извлечь k штук равно , а число способов, которыми можно выбрать n-k черных шаров из (N-K), равно .

Поэтому число исходов, благоприятных событию А, равно

и, следовательно, его вероятность, равная отношению благоприятных исходов к их общему числу, такова:

.

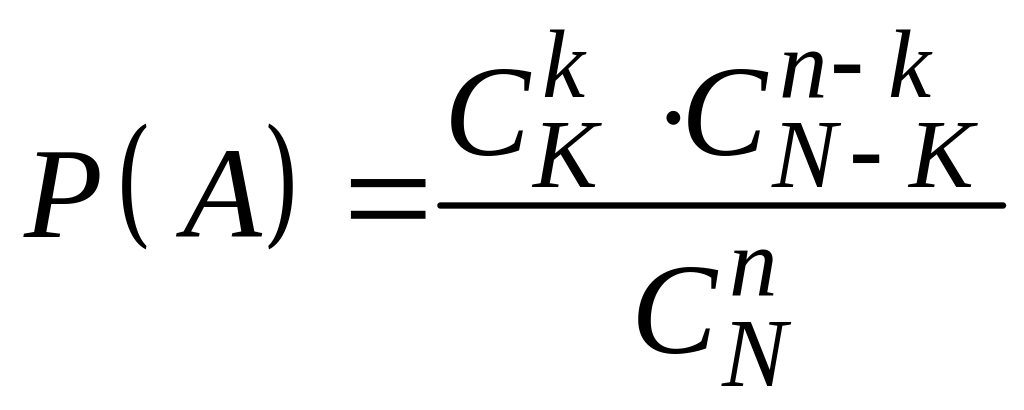1.5. АЛГЕБРА СОБЫТИЙ.

Случайное событие А интерпретируется попаданием элементарного события в множество А. Ввиду такого тесного соответствия между событием и множеством, над событиями можно производить операции, которые соответствуют логическим операциям или операциям над множествами.

Суммой событий А и В называется событие , состоящее из всех точек, принадлежащих или А, или В.

Произведением событий А и В называется событие либо АВ, состоящее из всех точек, принадлежащих А и В одновременно.

Разностью событий А и В называется событие , состоящее из всех точек, принадлежащих А, но не принадлежащих В. событие состоит в том, что А произошло, а В не произошло.

Событием, противоположным событию А, называется событие , состоящее из всех точек, не принадлежащих А. Событие состоит в том, что А не произошло.

П р и м е р. Брошена игральная кость. Обозначим через А событие, которое состоит в том, что выпало шесть очков. Событие  выпадение от одного до пяти очков.

Можно установить соответствие между событиями и логическими высказываниями. Так, событию А можно поставить взаимно однозначное соответствие высказывание "А произошло". Тогда А записывается в виде логической формулы, причем эту запись можно получить непосредственно из записи выражения А, если соединить события А_i, определяющие символами вместо союзов "или", "и" соответственно.

П р и м е р. Известна вероятность попадания двух стрелков в мишень. Найти вероятность одного попадания.

Попадание в мишень 1-го и 2-го стрелков обозначим . Тогда ровно одно попадание возможно в случае А:

Алгеброй событий называется некоторая система событий S, для которой:

а) и , то , , ,

б) .

Классическое определение вероятности характеризуется алгеброй событий S, которая конструируется из равновозможных попарно несовместных элементарных событий.

Если , то можно пользоваться формулой непосредственного подсчета вероятностей (1).

1.6 ТЕОРЕМА СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ

Теорема сложения вероятностей является теоремой только в рамках классической модели вероятностей. В общем случае это аксиома.

Теорема. Вероятность суммы двух событий равна сумме вероятностей минус вероятность произведения событий.

□ Обозначим опытное число возможных исходов n. Пусть событию

А благоприятствует m возможных исходов,

В благоприятствует k возможных исходов,

АВ благоприятствует f возможных исходов.

Тогда P(A + B) = Р(А) + Р(В) - Р(АВ) ■

Следствия:

1. Р(А + В)  Р(А) + Р(В).

2. Если события образуют полную группу попарно несовместных событий:

А₁ + ... + А_n = , то

Р(А₁ + ... + А_n) = 1

Р(А₁) + ... + Р(А_n) = 1

3. Вероятность противоположного события вычисляется по формуле:

.

1.7. ТЕОРЕМА УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ

Если к комплексу, при котором изучалась вероятность Р(А), добавить новое условие, состоящее в появлении события В, то получим другое значение вероятности Р(А|В)  условную вероятность события А  при условии, что произошло событие В.

Р(А)  безусловная вероятность.

П р и м е р. В урне 10 шаров: 6 белых и 4 черных. Из урны вынимают 2 шара. Введем обозначения: событие А заключается в том, что первый вынутый шар окажется белым, событие В  второй вынутый шар окажется белым. Тогда

Р(А) = Р(В) = 6/10, Р(В|А) = Р(А|В) = 5/9.

Теорема. Вероятность произведения двух событий А и В равна произведению вероятности одного из них на условную вероятность другого.

Р(АВ) = Р(А)Р(В|А) = Р(В)Р(А|В).

□ Пусть событию А благоприятствуют m элементарных исходов из n, событию В благоприятствуют k элементарных исходов из n.

Пусть событию А при условии, что В произошло, благоприятствуют r элементарных исходов.

.

Отсюда ,

аналогично . ■

Для рассмотренного примера определим вероятность того, что оба шара, вынутые из урны, окажутся белыми: P(AB) = P(A|B)P(B) = 1/3.

Событие А называется независимым от В, если его условная вероятность равна безусловной, т.е. P(A|B) = Р(А).

Следствия:

1. Из независимости А от В следует независимость В от А, т.е. взаимная независимость событий.

□ P(A|B) = Р(А),

P(A)Р(B|A) = Р(B)P(А|B),

Р(B|A) = Р(B),  В не зависит от А. ■

2. Формула умножения для независимых событий

P(AUB) = P(A)P(B).

3. События А и В, при Р(А) > 0, P(B) > 0, независимы тогда и только тогда, когда P(AUB) = = P(A)P(B).

4. События А₁ ... А_n называются независимыми в совокупности, если любое из событий А_p не зависит от произведения событий вида:

A_i1 A_i2 ... A_ir

Теорема умножения также является теоремой только для классической модели вероятностей. Во всех других случаях это аксиома.

П р и м е р. Две пушки стреляют по одному разу независимо по цели. Вероятность попадания в цель i-ой пушки Р(Аi) = 1/5. Какова вероятность того, что цель будет поражена?

Р е ш е н и е: