Вариант 1
Задание 1. Даны четыре вектора
в некотором базисе. Показать, что векторы
образуют базис и найти координаты
вектора
в этом базисе (систему решить тремя
способами: по правилу Крамера, матричным
методом, методом Жордана - Гаусса).
Вариант №1
Задание 2. Исследовать СЛАУ на совместность, найти общее и базисное решения. (Можно решить и исследовать методом Гаусса).
Вариант №1
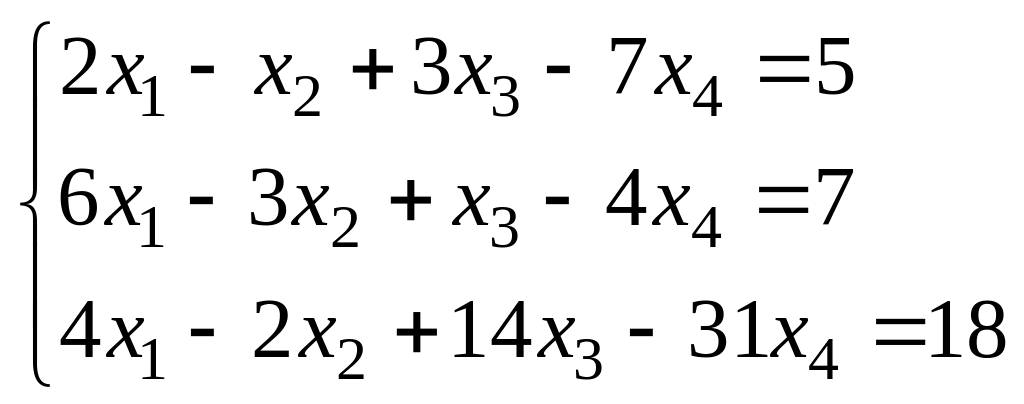
Задание 3. Найти собственные значения
и собственные векторы матрицы
.
Вариант №1
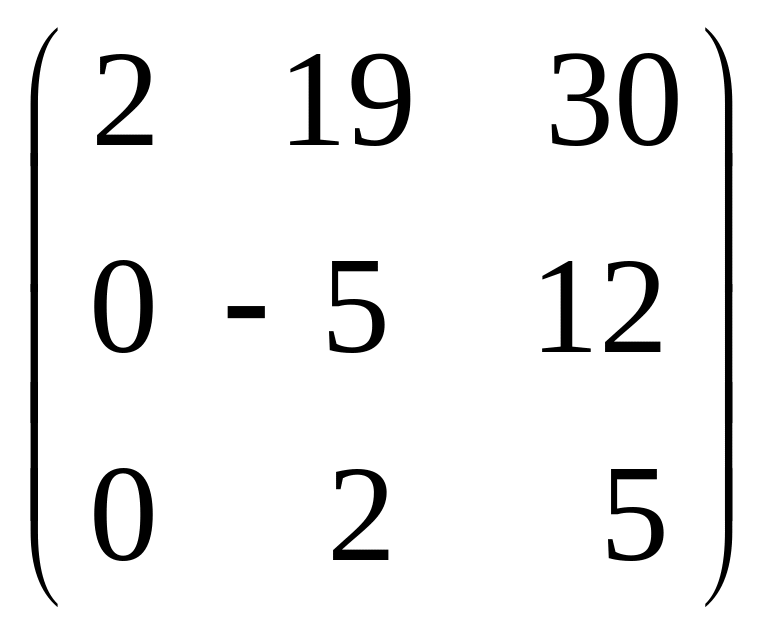
Здание 4. Даны вершины четырехугольника
.
1) Доказать, что четырехугольник является трапецией.
2) Найти уравнение стороны
.
3) Найти уравнение высоты, проведенной
из вершины
,
и длину этой высоты.
4) Найти острый угол при большем основании.
5) Найти уравнение средней линии трапеции.
6) Найти координаты точки
,
симметричной точке
относительно прямой
.
(Сделать рисунок в системе координат
).
Вариант №1
Задание 5. Даны вершины пирамиды .
1) Составить уравнение плоскости
.
2) Составить уравнение плоскости,
проходящей через точку
параллельно плоскости
.
3) Составить уравнение высоты пирамиды, проведенной из вершины .
4) Найти проекцию точки на плоскость .
5) Найти угол между ребром и плоскостью .
6) Найти расстояние от точки
до прямой
.
Вариант №1
Вариант 2
Задание 1. Даны четыре вектора в некотором базисе. Показать, что векторы образуют базис и найти координаты вектора в этом базисе (систему решить тремя способами: по правилу Крамера, матричным методом, методом Жордана - Гаусса).
Вариант №2
Задание 2. Исследовать СЛАУ на совместность, найти общее и базисное решения. (Можно решить и исследовать методом Гаусса).
Вариант №2
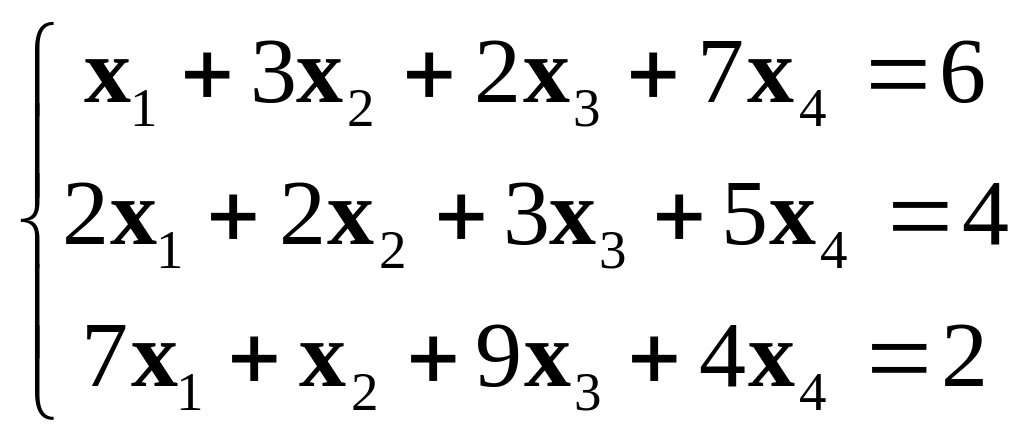
Задание 3. Найти собственные значения и собственные векторы матрицы .
Вариант №2
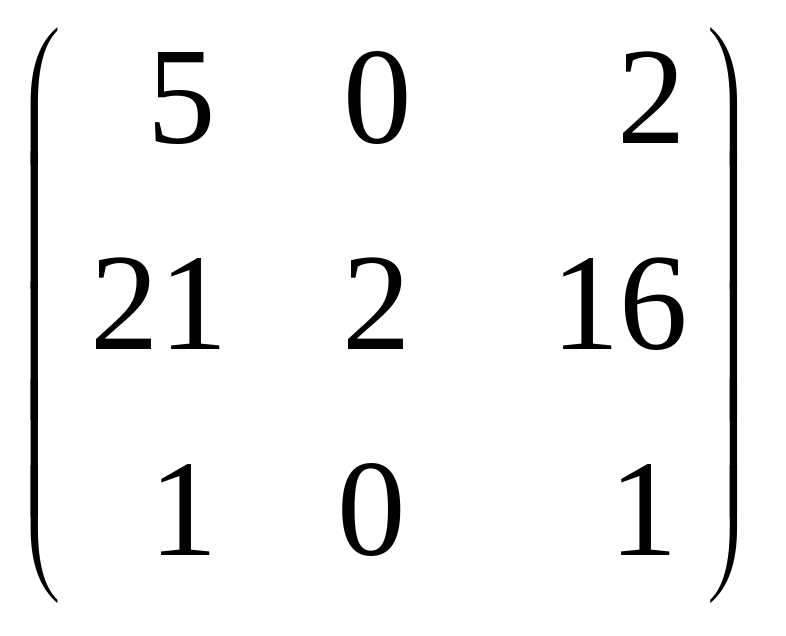
Здание 4. Даны вершины четырехугольника .
1) Доказать, что четырехугольник является трапецией.
2) Найти уравнение стороны .
3) Найти уравнение высоты, проведенной из вершины , и длину этой высоты.
4) Найти острый угол при большем основании.
5) Найти уравнение средней линии трапеции.
6) Найти координаты точки , симметричной точке относительно прямой . (Сделать рисунок в системе координат ).
Вариант №2
Задание 5. Даны вершины пирамиды .
1) Составить уравнение плоскости .
2) Составить уравнение плоскости, проходящей через точку параллельно плоскости .
3) Составить уравнение высоты пирамиды, проведенной из вершины .
4) Найти проекцию точки на плоскость .
5) Найти угол между ребром и плоскостью .
6) Найти расстояние от точки до прямой .
Вариант №2
Вариант 3
Задание 1. Даны четыре вектора в некотором базисе. Показать, что векторы образуют базис и найти координаты вектора в этом базисе (систему решить тремя способами: по правилу Крамера, матричным методом, методом Жордана - Гаусса).
Вариант №3
Задание 2. Исследовать СЛАУ на совместность, найти общее и базисное решения. (Можно решить и исследовать методом Гаусса).
Вариант №3
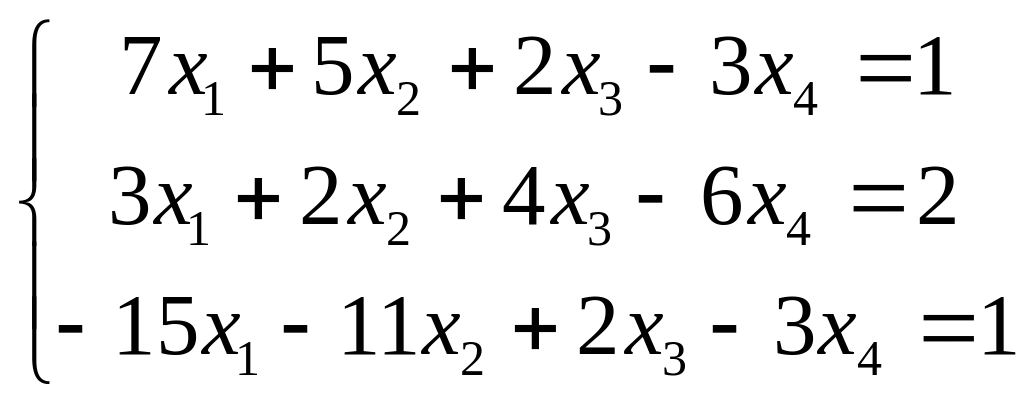
Задание 3. Найти собственные значения и собственные векторы матрицы .
Вариант №3
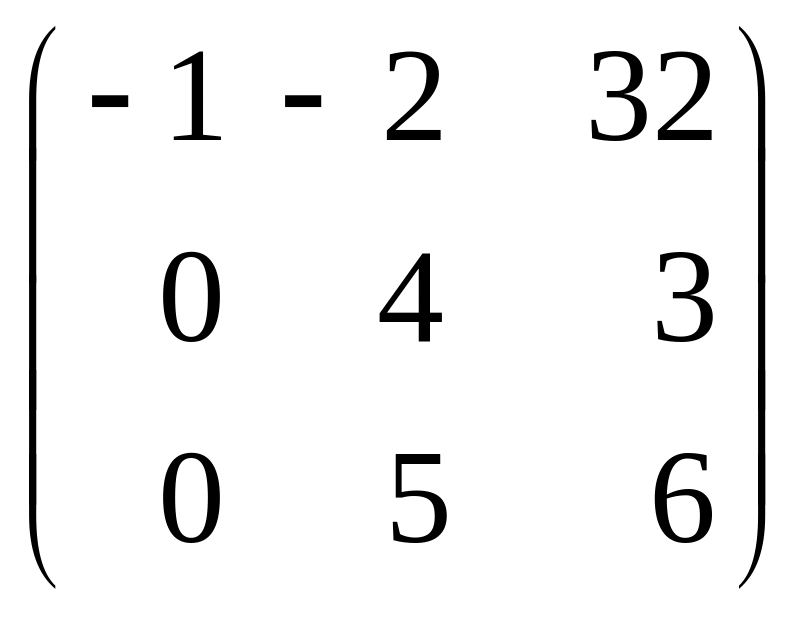
Здание 4. Даны вершины четырехугольника .
1) Доказать, что четырехугольник является трапецией.
2) Найти уравнение стороны .
3) Найти уравнение высоты, проведенной из вершины , и длину этой высоты.
4) Найти острый угол при большем основании.
5) Найти уравнение средней линии трапеции.
6) Найти координаты точки , симметричной точке относительно прямой . (Сделать рисунок в системе координат ).
Вариант №3
Задание 5. Даны вершины пирамиды .
1) Составить уравнение плоскости .
2) Составить уравнение плоскости, проходящей через точку параллельно плоскости .
3) Составить уравнение высоты пирамиды, проведенной из вершины .
4) Найти проекцию точки на плоскость .
5) Найти угол между ребром и плоскостью .
6) Найти расстояние от точки до прямой .
Вариант №3
