53

Аналіз довготермінових фінансових операцій: базові концепції і моделі оцінки

Придбання основних засобів, купівля/продаж цінних паперів, лізинг, отримання/погашення банківських кредитів, реалізація інвестиційних проектів – все це далеко не повний перелік важливих фінансових операцій, що часто здійснюються на довготерміновій основі та значною мірою визначають ефективність підприємницької діяльності.

Фактор часу і оцінка потоків платежів

«Сьогоднішній день вартує двох завтрашніх» (Б. Франклін)

1. Методи врахування фактору часу у фінансових операціях.

2. Оцінка потоків платежів.

   1. Фінансові операції з елементарними потоками платежів.

   2. Грошові потоки у вигляді серії рівних платежів.

   3. Грошові потоки у вигляді серії платежів довільної величини.

3. Розробка планів погашення кредитів

В результаті вивчення теми студенти повинні засвоїти:

• концепцію часової цінності грошей;

• методи врахування фактору часу у фінансових операціях;

• потоки платежів, їх види, властивості, характеристики;

• методи обчислення характеристик потоків платежів;

• фінансові функції ППП Excel;

• автоматизацію типових розрахунків в середовищі ППП Excel.

В умовах ринкової економіки при здійсненні довготермінових фінансових операцій важливу роль відіграє фактор часу. «Золоте» правило бізнесу стверджує: сума, отримана сьогодні, більша за таку ж саму суму, отриману завтра.

Проілюструємо «золоте» правило бізнесу з допомогою простої і наглядної моделі двохперіодного споживання видатного економіста І. Фішера на наступному умовному прикладі.

Приклад 1.1

Припустимо, що дехто Х володіє сумою в 10000 гр. од. і отримає таку ж саму суму через рік. Окрім того, існує можливість покласти грошів в банк на річний депозит, а також отримати кредит на такий самий термін. Банківська ставка по обох операціях дорівнює 10% річних. Визначити максимально можливе споживання для Х у поточному та майбутньому періодах.

На рис. 1.1 відображений графік моделі споживання для Х, що відображає всі рішення, які могли б бути прийняті в даній ситуації. Модель передбачає повну відсутність ризику та невизначеності при здійсненні будь-яких допустимих операцій. Наведемо необхідні пояснення.

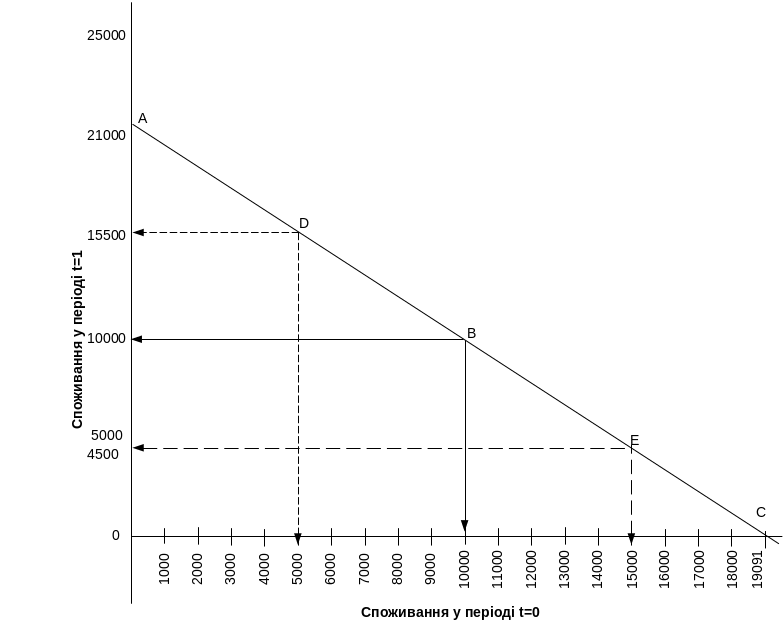
Рис. 1.1. Графік моделі споживання

Нехай – доходи, отримані в періоді t; – частина доходу, спрямована на споживання в періоді t; r – процентна ставка по банківських операціях; t=[0;1].

Найпростішим є той випадок, коли Х надає перевагу повному витрачанню своїх доходів, отриманих у відповідному періоді. Визначимо величину максимально можливого споживання для періодів t=0 і t=1:

, .

Цьому рішенню на графіку відповідає точка В з координатами (10000; 10000). Неважко помітити, що максимальне споживання за два періоди в цьому випадку буде дорівнювати:

.

Якщо ж частина отриманої в поточному році суми буде інвестована (покладена у банк під 10% річних), то доступні для споживання кошти у періоді t=1 складуть:

.

Одне із таких рішень, коли інвестується половина, отриманих у поточному періоді доходів (5000), на графіку позначено точкою D. При цьому обсяг споживання у періоді t=1 збільшиться із 10000 до 15500 (10000+(10000-5000)(1+0,1)).

Здійснена операція збільшить також і величину загального обсягу споживання за два періоди:

.

Припустимо, що Х вирішив помістити в банк увесь свій доход , отриманий у поточному періоді. Тоді загальна сума, доступна для споживання через рік, складе:

.

Отриманий результат відповідає максимально можливому в даному прикладі обсягу споживання за два періоди (точка А на рис.1.1).

При повній гарантії отримання 10000 через рік Х може збільшити споживання і в поточному періоді, скориставшись можливістю отримання кредиту за рахунок майбутніх доходів. Одному з таких рішень, коли споживання у поточному період збільшується за рахунок позичкових коштів (кредиту у 5000), на графіку відповідає точка Е. З урахуванням виплати 10% за кредит загальний обсяг споживання за два періоди при цьому буде дорівнювати:

.

Визначимо межу обсягу споживання у поточному періоді. Він буде дорівнювати отриманому доходу плюс максимальна сума кредиту, котра може бути погашена за рахунок майбутнього доходу . З урахуванням плати в 10% максимальна сума кредиту для Х дорівнює:

.

Тоді граничний обсяг споживання для періоду t=0:

(точка С на рис. 1.1).

Неважко помітити, що будь-які допустимі рішення цієї задачі лежать на прямій АС, заданій рівнянням:

.

Або, із врахуванням заданих значень:

.

Очевидно, що загальний обсяг споживання обмежений зверху максимально можливою сумою доходів за два періоди – точкою А з координатами (0; 21000). Точка С (19091; 0) відповідає максимально можливому споживанню у поточному періоді, перевищення якого призведе до того, що майбутніх доходів не вистачить, щоб погасити отриману позику.

Від’ємний нахил прямої, що дорівнює , показує, що кожна одиниця доходу, потрачена у поточному періоді, позбавляє можливості отримання у перспективі додаткового доходу у розмірі і зменшує обсяг майбутнього споживання на цю ж величину (тобто, на 1,1). З цієї точки зору володіння сумою S=10000 у майбутньому еквівалентно володінню сумою у теперішньому.

Відповідно, кожна одиниця доходу, інвестована у поточному періоді, дає можливість заробити суму у майбутньому, тобто час генерує гроші.

Таким чином, володіння сумою S=10000 у теперішньому в даних умовах еквівалентно володіння сумою у майбутньому.

Продемонстрована нерівноцінність двох однакових за величиною , але різних за часом отримання грошових сум – явище, широко відоме і усвідомлене у фінансовому світі. Його існування обумовлене цілим рядом причин. Деякими із них є:

• будь-яка наявна грошова сума в умовах ринку може бути одразу ж інвестована і впродовж деякого періоду часу принести дохід;

• навіть при невеликій інфляції купівельна спроможність грошей з часом знижується;

• у загальному випадку індивідиум надає перевагу поточному споживанню, а не майбутньому та ін.

Дослідження цього явища знайшли своє застосування у формулюванні принципу часової цінності грошей (time value of money), який є наріжним каменем у сучасному фінансовому менеджменті. Відповідно до цього принципу, сьогоднішні надходження цінніші за майбутні. Відповідно майбутні надходження володіють меншою цінністю порівняно із сучасними.

Із принципу часової цінності грошей випливають у крайньому випадку два важливих наслідки:

• необхідність врахування фактору часу при проведенні довготермінових фінансових операцій;

• некоректність (з точки зору аналізу довготермінових фінансових операцій) сумування грошових величин, що відносяться до різних періодів часу. (Подібне сумування допустиме, якщо фактор часу немає особливого значення, наприклад, у бухгалтерському обліку.)

Отже, необхідність врахування фактору часу при проведенні довготермінових фінансових операцій потребує застосування спеціальних кількісних методів його оцінки.