

3. Дифференциальные уравнения звеньев.
Звенья – соединенные в определенной последовательности элементы и устройства, из которых состоит САУ.
Линейная непрерывная стационарная система с сосредоточенными параметрами – система, которая в целом так же, как и отдельные звенья, описывается ЛОДУ с постоянными коэффициентами.
Если x1 – входной сигнал, а x2 – выходной (сигналы интерпретируются как функции текущего времени t) то, звено в общем случае описывается ДУ следующего вида:
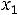 ,
,
где 

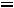







 .
.
Коэффициенты ai, bi зависят от конструктивных параметров звена. Порядок ДУ n так же будет определять порядок звена, как правило n≤2.
Для математического описания процессов в звене следует задавать начальные условия.
Уравнение звеньев в стандартной форме:
пусть 





















 , тогда уравнение (1):
, тогда уравнение (1):
Так же уравнения (2) и (1) можно записать в операторном (символическом) виде,
вводя дифференциальный оператор |
|
|
такой, что |
|
|
|
, тогда уравнение |
||
|
|
|
|
|
|||||
(1) примет вид: |
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|||||
обозначив левую скобку A(p), а правую B(p) получим |
. |
||||||||
По виду ДУ (1) звенья делятся на: |
|
|
|
|
|
|
|
||
-позиционные ( |
); |
|
|
|
|
|
|
||
-дифференцирующие( |
); |
|
|
|
|
||||
-интегрирующие( |
); |
|
|
|
|
|
|
||
Уравнения в пространстве состояний:
D – матрица обхода, в реальных системах D=[0]
A – диагональная матрица Фробениуса
