12. Передаточные функции и дифференциальные уравнения систем.
Обозначим произведение W1(s) и W2(s) через W(s) – передаточная функция разомкнутой системы, (ГОС – разомкнута,
f=0) 
;
Если характеристическое уравнение системы L(λ)=0 не содержит нулевых корней, то САУ статическая. При наличии нулевых корней передаточную функцию можно
представить в виде 
, где L0(λ)=0 не содержит нулевых корней, ν –
количество нулевых корней уравнения L(λ)=0. САУ с передаточной функцией (2) – астатическая САУ с астатизмом ν-го порядка.(1) является частным случаем (2).
Для замкнутых САУ (ГОС замкнута, f≠0):
Из (3): 
Ф(s) – главная передаточная функция замкнутой системы
Фf(s) – передаточная функция замкнутой системы по возмущению Фe(s) – передаточная функция замкнутой системы по ошибке тогда 
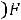
Если W(s) представлена в виде (1), то 
,
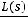
где 
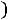
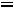
, D(s) – характеристический полином замкнутой САУ, D(λ)=0 характеристическое уравнение замкнутой САУ.
Если в уравнении (5) сделать подстановку выражений (7) получим
D(s)Y(s)=KN(s)V(s)+R(s)F(s), перейдя к оригиналам (s→p) получим ДУ замкнутой САУ: D(p)y(t)=KN(p)v(t)+R(p)f(t). Порядок ДУ будем называть порядком САУ. Полученное ДУ описывает поведение системы в динамическом режиме, частным случаем которого является статический (установившийся) режим. Полагая y, f, v=const(тогда их производные равны нулю, что соответствует p= 0 в полиномах D, N, R) получи уравнение статического режима: D(0)y=KN(0)v+R(0)f.
N(0)=1, D(0)=K – астатическая САУ, D(0)=K+1 – статическая САУ. Для астатических САУ (ν≠0) 
Для статических САУ (ν=0) 
Значение величины R(0) зависит от вида передаточных функций W1(s), W2(s).
//Временные характеристики замкнутых САУ (в вопросах нету, но пусть будут)