4. Линеаризация уравнений динамики звеньев.
Реальные устройства САУ обычно нелинейны. Линеаризация – операция замены нелийненых САУ линейными. Наиболее распространѐнный – способ, базирующийся на разложении в ряд Тейлора.
Пусть звено САУ описывается |
, где x1 – входной, x2 – |
выходной сигналы. |
|
Рассмотрим установившийся режим работы звена когда на входе действует
постоянный сигнал |
, а на выходе |
. Связь |
||||
установившихся значений сигналов x1 и x2 задается уравнением |
||||||
установившегося режима |
|
|
|
|
|
|
Отклонения от установившегося режима |
|
|
|
|
. |
|
|
|
|||||
Разложим (1) в ряд Тейлора относительно координат |
и : |
|||||
,
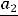
где
Учитывая, что 
и 
, и пренебрегая величинами второго и большего порядков малости, получим
(2) –
линеаризованное уравнение.
Уравнение (2) – уравнение касательной к исходной кривой в точке линеаризации (А).
Особенности линеаризации:
-возможна, если исходная нелинейная функция в точке разложения является аналитической (дифференцируема бесконечное число раз).
-коэффициенты a1 и b1зависят от координат точки линеаризации.
-линеаризованное уравнение тем ближе к исходному, чем меньше отклонение переменных.