6. Частотные характеристики звеньев.
Частотные характеристики определяют динамические свойства звеньев при воздействии на них гармонических сигналов. Частотные характеристики получаются из передаточной функции при s=jw. 
. Т.е. 
- прямое преобразование Фурье от w(t).
Комплексная функция 
частоты ω – АФЧХ звена
– АЧХ 
- ФЧХ
U(ω) – вещественная частотная характеристика, V(ω) – мнимая.
.
Если на вход звена с передаточной функцией W(s) подать сигнал 
, то в установившемся режиме выходной сигнал: 
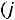
, т.е. той же частоты, но измененных амплитуды и фазы.
Т.о. АЧХ показывает изменение амплитуды, а ФЧХ – изменение фазы.
Частотные характеристики обладают следующими свойствами: U(-ω)=U(ω); A(-ω)=A(ω) – чѐтные характеристики V(-ω)=-V(ω); φ(-ω)=-φ(ω) – нечетные характеристики
В силу этого АФЧХ строится на комплексно плоскости, при изменении ω от 0 до ∞ (при ω<0, вторую часть достраивают симметрично первой относительно оси абсцисс).
На практике часто применяются ЛАЧХ и ЛФЧХ.//[Б] – изменение уровня мощности сигнала на декаду.