Министерство образования Республики Беларусь

Учреждение образования

«Белорусский государственный университет

информатики и радиоэлектроники»

Кафедра информационных технологий автоматизированных систем

контрольная работа

по дисциплине

ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

по теме: Временные характеристики линейных систем

Ильюкевич Виктор

ст. гр. 700621с

Минск 2011

Задание

Постройте графики импульсной переходной и единичной переходной функции. Приведите программу вычислений.

Решение

Построим график импульсной переходной функции для системы, заданной дифференциальным уравнением:

x" + 0.2x' + 0.02x = 0.1y' + 0.03y

Код программы:

>> M=[0.1 0.03];

>> D=[1 0.2 0.02];

>> derD=polyder(D)

derD =

2.0000 0.2000

>> Alph=roots(D)

Alph =

-0.1000 + 0.1000i

-0.1000 - 0.1000i

>> A1=polyval(M, Alph(1))/polyval(derD, Alph(1))

A1 =

0.0500 - 0.1000i

>> A2=polyval(M, Alph(2))/polyval(derD, Alph(2))

A2 =

0.0500 + 0.1000i

>> t=0:2:80;

>> k=A1*exp(Alph(1)*t)+A2*exp(Alph(2)*t);

>> plot(t, k);

>> grid

Рисунок 1. Окно программы

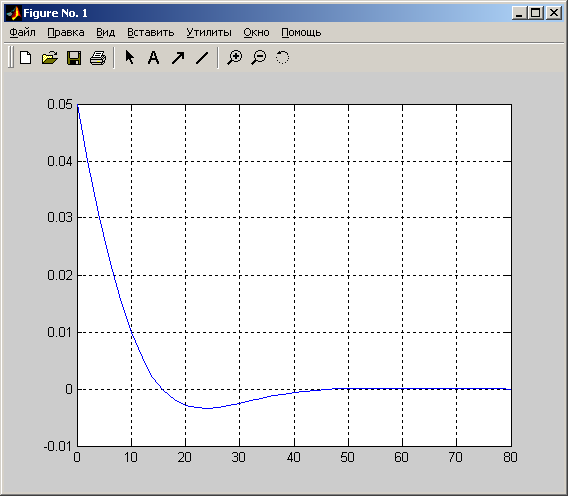
Рисунок 2. График импульсной переходной функции

Наряду с импульсной переходной функцией в качестве характеристики линейной системы используется и единичная переходная функция h(t) или просто переходная функция (переходный процесс). Функцию h(t) можно представить себе как реакцию системы x(t) на единичное воздействие y(t)=1(t)

Для определения единичной переходной функции надо взять обратное преобразование не от передаточной функции , а от

Код программы (в продолжение ранее введённого кода)

>> A11=(polyval(M, Alph(1))/polyval(derD, Alph(1)))/1

A11 =

0.0500 - 0.1000i

>> A12=(polyval(M, Alph(2))/polyval(derD, Alph(2)))/2

A12 =

0.0250 + 0.0500i

>> k1=A12*exp(Alph(1)*t)+A12*exp(Alph(2)*t);

>> plot(t, k1);

>> grid

Рисунок 3. Окно программы

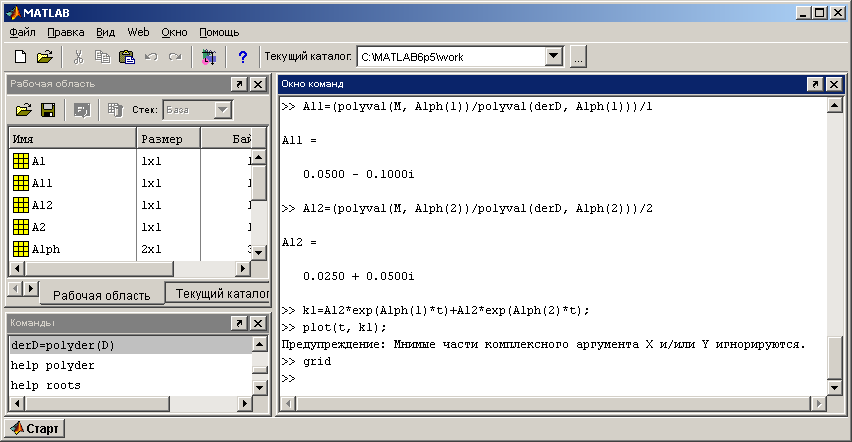
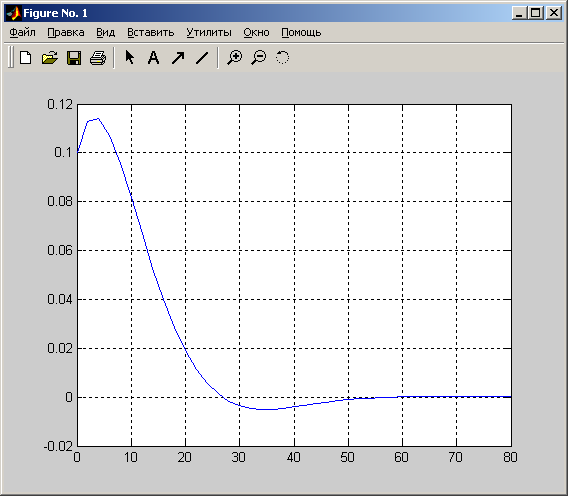
Рисунок 4. График единичной переходной функции