Контрольная работа

Добавил:

Kaz Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский государственный университет информатики и радиоэлектроники

Предмет:

Теория автоматического управления

Файл:

ф(w) = −arctg

(T1 T2 + T1 T3 + T2 T3) w2 úù

+ T2 + T3) w −

T1 T2 T3 w û

.pdf

Скачиваний:

Добавлен:

15.06.2014

Размер:

369.44 Кб

Скачать

☆

1 / 31 2 3 > Следующая >>>

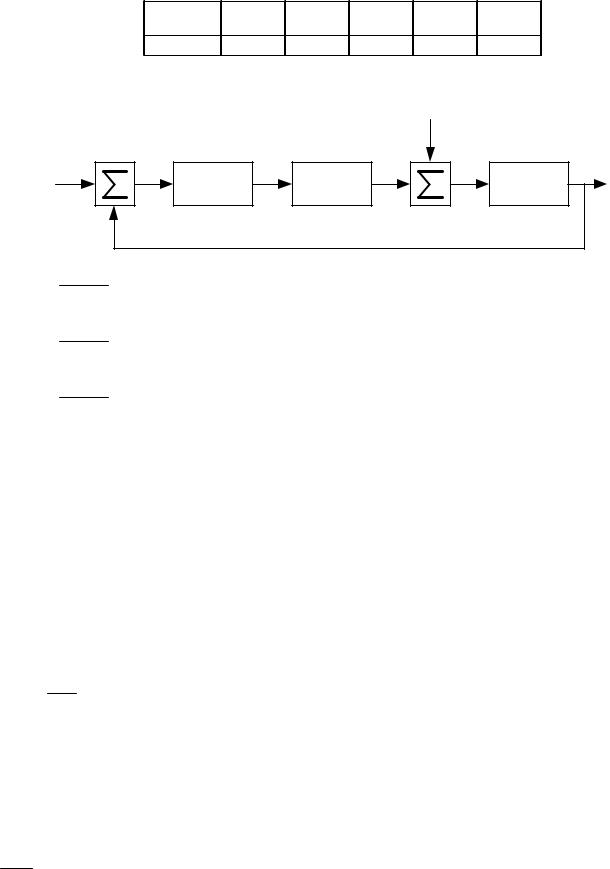
					Исходные данные:
			Номер	T 1	T 2	T 3	K1	K3
			варианта	T 1	T 2	T 3	K1	K3
			варианта
			29	0,5	1,5	0,8	2,5	3,8
Структурная схема линейной САУ имеет вид:							f
							f
		v+	е			+	-	y
		v+	е		W2(s)	+		y
			W1(s)		W2(s)			W3(s)
		-
W1	(s) =	K1
W1	(s) =	T1 s + 1
		T1 s + 1
W2	(s) =	K2
W2	(s) =	T2 s + 1
		T2 s + 1
W3	(s) =	K3
W3	(s) =	T3 s + 1
		T3 s + 1
1. Найдем передаточные функции разомкнутой и замкнутой систем:
1.1 Определим передаточную функцию разомкнутой системы при f=0 и e=v:

W(s) =	Y(s)	=	V(s) W1(s) W2(s) W3(s)				= W (s) W (s) W (s)
W(s) =		=					= W (s) W (s) W (s)
	V(s)				V(s)		1	2	3
	V(s)				V(s)
W(s) = W1(s) W2				(s) W3	(s) =		K1 K2 K3
W(s) = W1(s) W2				(s) W3	(s) =	(T1 s + 1) (T2 s + 1) (T3 s + 1)
						(T1 s + 1) (T2 s + 1) (T3 s + 1)

1.2 Определим главную передаточную функцию замкнутой системы при f=0:

Ф(s) = Y(s) V(s)

Выражение для сигнала рассогласования имеет вид:

E(s) = V(s) − Y(s)

Y(s) = W(s) E(s)

Исключим из этих двух выражений E(s):

Y(s) = V(s) − Y(s)

W(s)

Y(s) + Y(s) = V(s)

W(s)

Y(s) + W(s) Y(s) = V(s)

W(s)

Y(s) (1 + W(s)) = V(s)

W(s)

Y(s) = V(s) 1 + W(s)

Ф(s)

W(s)

1 + W(s)

Ф(s)

K1 K2 K3

(T1 s + 1) (T2 s +

1) (T3 s + 1) ê

+ 1ú

ë(T1 s + 1) (T2 s + 1) (T3 s + 1)

Ф(s)

K1 K2 K3

T T T s3

+ (T T + T T + T T )

s2 + (T + T + T ) s + K

K K + 1

1.3 Определим передаточную функцию замкнутой системы по ошибке при f=0:

E(s) Фe(s) = V(s)

E(s) = V(s) − Y(s)

Y(s) = W(s) E(s)

Исключим из этих двух выражений Y(s):

E(s) = V(s) − W(s) E(s) E(s) + W(s) E(s) = V(s) E(s) (1 + W(s)) = V(s)

E(s) =				V(s)
E(s) =		1 + W(s)
Фe(s)	=		1
Фe(s)	=		1 + W(s)
Фe(s) =						1
Фe(s) =					K1	K2 K3
					K1	K2 K3
							+ 1
				(T1 s + 1) (T2 s + 1) (T3 s + 1)			+ 1
Фe(s) =				T1 T2 T3 s3 + (T1 T2 + T1 T3 + T2 T3) s2 + (T1 + T2 + T3) s + 1
Фe(s) =			T1 T2 T3 s3 +			(T1 T2 + T1 T3 + T2 T3) s2 + (T1 + T2 + T3) s + K1 K2 K3 + 1
			T1 T2 T3 s3 +

1.4 Определим передаточную функцию замкнутой системы по возмущению при v=0:

Y(s) Фf (s) = F(s)

Eвозм(s) = −F(s) − W1(s) W2(s) Y(s)

Y(s) = W3(s) Eвозм(s)

Исключим из этих двух выражений Eвозм(s):

Y(s)

W3(s) = −F(s) − W1(s) W2(s) Y(s)

Y(s)

W3(s) + W1(s) W2(s) Y(s) = −F(s)

Y(s) + W(s) Y(s) = −F(s)

W3(s)

Y(s) (1 + W(s)) = −F(s)

W3(s)

Y(s) = −F(s)			W3(s)
Y(s) = −F(s)		1	+ W(s)
Фf (s) = −	W3		(s)
Фf (s) = −	1 + W(s)
Фf (s) = −					K3
Фf (s) = −			é		K1 K2 K3	ù
			é		K1 K2 K3	ù
	(T3 s + 1) ê					+ 1ú
	(T3 s + 1) ê					+ 1ú
				ë(T1 s + 1) (T2 s + 1) (T3 s + 1)		û

K3 T1 T2 s2 + (K3 T1 + K3 T2) s + K3

Фf (s) = −

T1 T2 T3 s3 + (T1 T2 + T1 T3 + T2 T3) s2 + (T1 + T2 + T3) s + K1 K2 K3 + 1

2. Определим необходимое значение K2, удовлетворяющее критерию устойчивости:

2.1 Найдем характеристическое уравнение замкнутой системы:

(1 + W(s)) Y(s) = W(s) V(s)

Приравняем левую часть уравнения к нулю и найдем характеристическое уравнение замкнутой системы:

1 + W(s) = 0

1 + W(s) =

T1 T2 T3 s3 + (T1 T2 + T1 T3 + T2 T3) s2 + (T1 + T2 + T3) s + K1 K2 K3 + 1

T1 T2 T3 s3 + (T1 T2 + T1 T3 + T2 T3) s2 + (T1 + T2 + T3) s + 1 T1 T2 T3 s3 + (T1 T2 + T1 T3 + T2 T3) s2 + (T1 + T2 + T3) s + K1 K2 K3 + 1 = 0 a3 = T1 T2 T3

a2 = T1 T2 + T1 T3 + T2 T3 a1 = T1 + T2 + T3

a0 = K1 K2 K3 + 1

Матрица Гурвица имеет вид:

æ a2		a0	0	ö
ç		a1		÷
ç a3		a1	0	÷
ç	0	a	a	÷
è		2	0	ø

Так как матрица Гурвица является матрицей 3-го порядка, то выражения для определителей имеют вид:

= a2

D1 = T1 T2 + T1 T3 + T2 T3

æ a2

a0 ö

ç a

D = T T

2 + T 2 T + T T

2 + T

2 T + T T

2 + T

2 T + 2 T T T − K K K

T T T

æ a2

0 ö

ç a

0 ÷

D3 = (K1 K2 K3 + 1)

T2 + T1 T3

T3 + 2 T1

èT1

+ T1

T3 + T2 T3

T2 T3 − K1 K2 K3 T1 T2 T3ø

2.2 В общем виде критерий устойчивости Гурвица имеет вид - система устойчива, если при a3>0:

D1 > 0 D2 > 0 D3 > 0

2.3 Найдем максимальное граничное значение коэффициента усиления K2, при котором система еще устойчива:

Решая уравнение D2=0 найдем K2крит:

T T 2		+ T		2	T + T T			2 + T	2 T + T T 2			+ T 2	T + 2 T T T − K K K						3	T T T = 0
1	2		1		2	1	3	1	3	2	3	2	3	1	2	3	1	2	3	1	2	3
				T	2 T + T		2	T + T T		2 + 2 T T T + T T 2 + T						2 T + T T 2
K			=	1	2	1		3	1 2		1	2 3	1 3		2	3	2	3		= 1.049
K			=																	= 1.049
2.крит										K1 K3 T1 T2 T3
										K1 K3 T1 T2 T3

С учетом коэффициента запаса устойчивости системы а=2 найдем K2:

K =	K2.крит	=	1.049	= 0.525

2	a		2

3 Найдем аналитические выражения и постоим графики:

3.1 W(w) амплитудно-фазовой частотной характеристики (АФЧХ) разомкнутой системы:

W(w) =

K1 K2 K3

(1 + T1 j w) (1 + T2 j w) (1 + T3 j w)

W(w) =

K1 K2 K3

−j T1 T2 T3 w3 − (T1 T2 + T1 T3 + T2 T3) w2 + j (T1 + T2 + T3) w + 1

W(w) =

K1 K2 K3

é(T + T + T

)

w − T T T w3ù

é1 −

(T T + T T + T T

)

w2ù

ë 1

1 2 3

1 2

1 3

2 3

W(w) =

K1 K2 K3

é(T + T + T

)

w − T T T w3ù

é1 −

(T T + T T + T T

)

w2ù

ë 1

1 2 3

1 2

1 3

2 3

умножим числитель и знаменатель на комплексно-сопряженное знаменателю

значение:

é−j

é(T + T + T

) w − T T T w3ù + é1 −

(T T + T T + T T

)

w2ùù

W(w) = W(w)

1 2 3

û ë

1 2

1 3

2 3

ûû

é−j

é(T + T + T

) w − T T T w3ù + é1 −

(T T + T T + T T

)

w2ùù

ë ë

1 2 3

û ë

1 2

1 3

2 3

ûû

K K

é1 − (T T + T T + T T ) w2ù − j K K K

é(T + T + T )

w − T T T w3ù

W(w) =

1 2 3

1 2

1 3

2 3

1 2 3

æT

2 T

2 + T

2 + T 2

2ö + w2 æT 2

+ T 2

+ T

2ö + T

2 T 2

w6 + 1

1 2

1 3

2 3 ø

3 ø

1 2 3

Wвещ(w) =

K1 K2 K3 ëé1 − (T1 T2 + T1 T3 + T2 T3) w2ûù

w4 æT

T 2

+ T 2

T 2 + T 2 T 2ö + w2 æT

2 + T 2 + T 2ö + T 2

T 2

w6 + 1

1 2

1 3

3 ø

è 1

3 ø

1 2 3

−K

K K

é(T + T + T )

w − T T T w3ù

Wмним(w) =

1 2 3

æT

2 T

+ T

T 2 + T 2

2ö + w2 æT 2 + T 2

+ T

2ö

+ T

2 T

w6 + 1

1 2

1 3

2 3 ø

3 ø

1 2 3

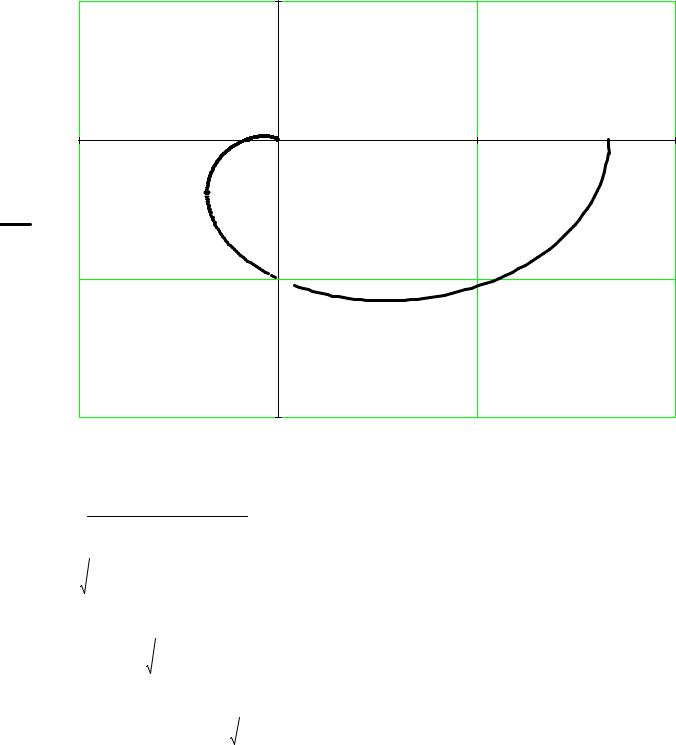
Построим график амплитудно-фазовой частотной характеристики (АФЧХ) разомкнутой системы на интервале от 0 до +oo рад/с, по вертикальной оси будем откладывать мнимую, а по горизонтальной оси - вещественную часть АФЧХ:

	ϖ = ∞		ϖ = 0
	ϖ = ∞
− 3	0	3	6

Wмним(w)

−3

− 6

Wвещ(w)

3.2 |W(w)| амплитудно-частотной характеристики (АЧХ) разомкнутой системы:

Wмод(w) = Wвещ(w)2 + Wмним(w)2

éK

K K

é1 − (T T + T T + T T )

w2ùù

2 + é−K K K

é(T + T + T )

w − T T T w3ùù2

W (w) =

ûû

2 3

ûû

мод

w4 æT 2

T 2

+ T 2 T 2 + T 2

T 2ö + w2 æT

2 + T 2

+ T

2ö

+ T 2

T 2

+ 1

è 1 2

1 3

2 3 ø

3 ø

1 2 3

K K

é1 −

(T T + T T + T T )

w2ù2

+ é(T + T + T ) w − T T T w3ù2

Wмод(w) =

1 2 3

1 2

1 3

2 3

1 2 3

æT 2

2 + T 2 T 2

+ T 2

T 2ö + w2

æT 2

+ T

+ T 2ö

+ T

2 T 2 T

2 w6

+ 1

1 2

1 3

2 3

è 1

3 ø

1 2 3

Wмод(w) =

K1 K2 K3

ëé1 + (T1 w)2ûù ëé1 + (T2 w)2ûù ëé1 + (T3 w)2ûù

w4 æT

2 T

+ T

2 T

2 + T 2 T

2ö

+ w2 æT 2 + T 2

+ T

2ö + T

2 T 2

w6 + 1

1 2

1 3

2 3 ø

3 ø

1 2 3

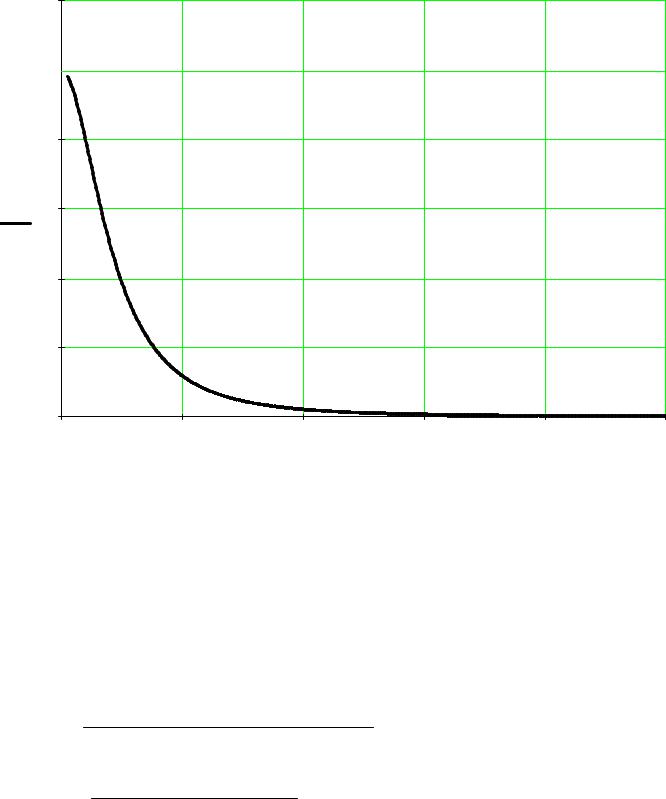
Построим график амплитудно-частотной характеристики (АЧХ) разомкнутой системы на интервале 0...10 рад/с (из соображений наглядности графика), по вертикальной оси будем откладывать амплитуду, а по горизонтальной оси - частоту:

Wмод(w)3

0	2	4	6	8	10
			w рад/с

3.3 ф(w) фазо-частотной характеристики (ФЧХ) разомкнутой системы:

æ Wвещ(w) ö

ф(w) = arctgç

(w)

мним

(T1 T2+T1

T3+T2 T3)

2ù

K1 K2 K3 ë1−

w û

æT 2 T

2+T

2 T 2+T

2ö

+w2

æT

2+T

2ö

2 T 2 w6+1

ф(w) = arctg

è 1 2

1 3

2 3

è 1

1 2 3

é(T1+T2+T3)

− K1 K2 K3

w−T1 T2 T3 w

æT 2 T

2+T

2 T 2+T

2ö

+w2

æT

2+T

2ö

2 T 2 w6+1

è 1 2

1 3

2 3

è 1

1 2 3

é éK1 K2 K3 é1 − (T1 T2 + T1 T3 + T2 T3) w2ùù ù

ф(w) = arctgê ë ë ûû ú êëéë−K1 K2 K3 éë(T1 + T2 + T3) w − T1 T2 T3 w3ùûùûúû

é é1 − (T1 T2 + T1 T3 + T2 T3) w2ù ù ф(w) = arctgê− ë û ú êë éë(T1 + T2 + T3) w − T1 T2 T3 w3ùûúû

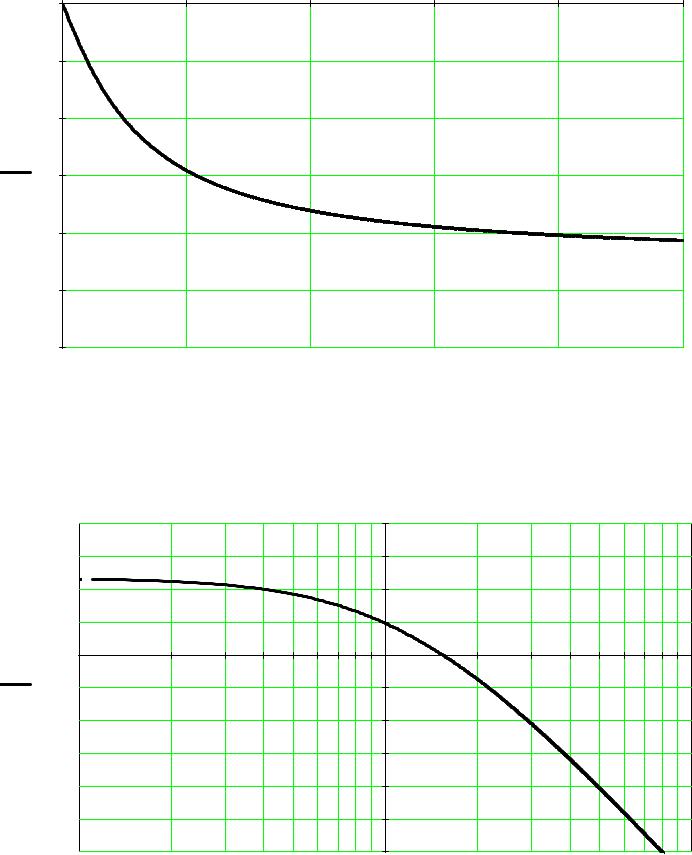
Построим график фазо-частотной характеристики (ФЧХ) разомкнутой системы на
интервале 0...10 рад/с (из соображений наглядности графика), по вертикальной оси
будем откладывать фазу в градусах, а по горизонтальной оси - частоту:
	0	2	4	6	8	10
− 60
− 120
ф(w)
град − 180
− 240
− 300
− 360
				w рад/с
3.4 Построим в логарифмическом масштабе график амплитудно-частотной
характеристики (ЛАЧХ) разомкнутой системы на интервале 0.1-10 рад/с (из
соображений наглядности графика), по вертикальной оси будем откладывать
амплитуду, а по горизонтальной оси - частоту:
ЛАЧХ(w)	= 20log(Wмод(w))
				24
				18
				12
				6
ЛАЧХ(w)	0.1			1		10
ЛАЧХ(w)				− 6
дБ				− 6
дБ
				− 12
				− 18
				− 24
				− 30
				− 36
				w рад/с

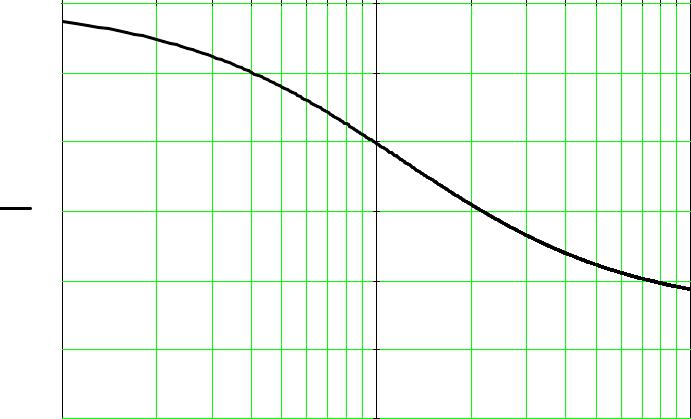
3.5 Построим в логарифмическом масштабе график фазо-частотной характеристики
(ЛФЧХ) разомкнутой системы на интервале 0.1-10 рад/с (из соображений наглядности
графика), по вертикальной оси будем откладывать фазу в градусах, а по
горизонтальной оси - частоту:
0.1	1	10
	− 60
	− 120
ф(w)	− 180
град	− 180
град
	− 240
	− 300
	− 360
	w рад/с

3.6 P(w) вещественной частотной характеристики замкнутой системы:

Ф(w)

K1 K2 K3

T1 T2 T3 (j w)3 + (T1 T2 + T1 T3 + T2 T3) (j w)

2 +

(T1 + T2 + T3) j w + K1 K2 K3 + 1

Ф(w)

K1 K2 K3

T1 T2 T3 (j w)3 + (T1 T2 + T1 T3 + T2 T3) (j w)

2 +

(T1 + T2 + T3) j w + K1 K2 K3 + 1

Ф(w)

K1 K2 K3

−j T1 T2 T3 w3 − (T1 T2 + T1 T3 + T2 T3) w2 + j (T1 + T2 + T3) w + K1 K2 K3 + 1

Ф(w) =

K1 K2 K3

j é(T

+ T + T

) w − T

T T

w3ù + éK

+ 1 − (T T

+ T

T + T T )

w2ù

ë 1

1 2 3

û ë 1

2 3

1 2

1 3

2 3

умножим числитель и знаменатель на комплексно-сопряженное знаменателю

значение:

éK K

K + 1 −

(T T + T T + T T ) w2ù

− j

é(T + T + T )

w − T T T w3ù

Ф(w) = Ф(w)

ë 1

1 2

1 3

ë 1

2 3

éK K

K + 1 −

(T T + T T + T T ) w2ù

− j

é(T + T + T )

w − T T T w3ù

ë 1

2 3

1 2

1 3

2 3

ë 1

1 2 3

упростим выражение для знаменателя:

A6 = T12 T22 T32

A4 = æèT12 T22 + T12 T32 + T22 T32öø

A =

æT 2

− 2 K K K

T T − 2 K K K T T + T

2 − 2 K K K

T T + T 2ö

1 2

3 1 2

1 2 3 1 3

1 2

3 2 3

A0 = (K1 K2 K3 + 1)2

K K K

ééK K

K + 1 −

(T T + T T + T T ) w2ù − j

é(T + T + T )

w − T T T w3ùù

Ф(w)

1 2 3

ëë

2 3

1 2 1 3

2 3

1 2

1 2 3

ûû

A6 w6 + A4 w4 + A2 w2 + A0

K1 K2 K3

K3 +

1 − (T1 T2 + T1 T3 +

2ù

Фвещ(w) =

ëK1 K2

T2 T3) w û

A6 w6 + A4 w4 + A2 w2 + A0

K K

é(T + T + T )

w − T T T w3ù

(w)

= −

ë 1

1 2

мним

A6 w6 + A4 w4 + A2 w2 + A0

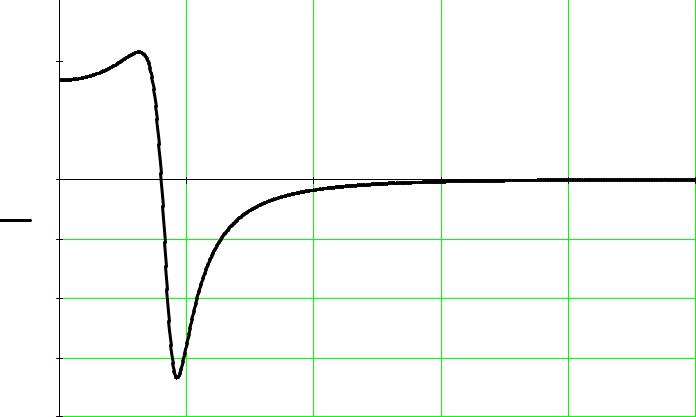
P(w) = Фвещ(w)

1.5

0.5

P(w)

− 0.5

− 1

− 1.5

− 2

w рад/с

1 / 31 2 3 > Следующая >>>

Соседние файлы в предмете Теория автоматического управления

#
15.06.2014113.66 Кб42Контрольная работа 1 Временные характеристики линейных систем.doc
#
15.06.2014172.03 Кб36Контрольная работа 2 Частотные характеристики систем.doc
#
15.06.2014369.44 Кб64Контрольная работа.pdf
#
15.06.2014411.73 Кб70Образец контрольной работы 2 по ТАУ.pdf
#
15.06.2014338.43 Кб96практика матлаб (Мет пособие).doc
#
15.06.20146.69 Mб54шпоры full [3232 вопросов].doc