32. Воздействие узкополосого шума на линейный амплитудный детектор.
Общие положения
Напряжение на вых. детектора воспроизводит огибаю щую амплитуд ВЧ колебания на входе.Рассмотрим лин.амп.дет. Статистические характеристики шума на выходе лин.амп.дет. З- н распределения вер-тей шума на вых. амп. дет. Огибающая,хар-щаяся з-ном распред. наз.з-
ном Релея и имеет вид: 
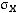. Спектральная плотность мощности шума на выходе амплитудного детектора.
Метод определения Wy(ω)
|
|
j |
|
1) W y ( ) |
B y ( ) e |
d |
по теореме Винера-Хинчина |
2) |
B y ( ) |
f ( x1 ) f ( x2 ) p ( x1 x2 |
) dx1 dx2 |
Учитывая з-н распределения,узкополосность сигнала на вх. (норм з -н распред.) и при Mx=0, можно записать:
|
|
|
|
|
|
x1 2 x2 2 |
2 |
x1 |
x2 r x ( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 D x |
1 |
r x ( |
) 2 |
|
R y ( ) |
|
|
|
|
f ( x1 ) f ( x2 ) e |
|
|
|
dx1 dx2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|||||||
3) |
2 D x |
1 |
r x ( ) 2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Полученный интеграл не подлежит прямому вычислению. Один из методов вычисления
предполагает разложение |
|
p ( x1 x2 ) |
в |
ряд по |
ортогональным полиномам (Эрмита).Полином |
|||||||
Эрмита: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
n |
|
|
|
|
|
|
|
|
( 1 ) n |
e x |
|
|
d |
|
|
|
|
|
|
|
H n ( x) |
|
|
|
|
|
|
|
|
|
|
||
|
|
dx n |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
n |
x2 |
|
x2 |
1) H0(x)=1 |
|
2) |
H1(x)= |
( |
1 ) |
|
e |
2x e |
=2x |
|||
|
|
|
|
|
|
|||||||
При этом получается след. формула для ковариац. ф -ции:
|
|
D x |
|
r 0 ( ) |
|
|
|
|
2 |
|
|||
|
|
|
1 3 |
5 ... |
( 2 k |
3 ) |
|
2 k |
|||||
B y |
( ) |
|
|
1 |
|
|
|
|
|
|
|
r 0 ( |
) |
|
|
|
2 |
4 ... |
2 k |
|
|||||||
|
2 |
|
4 |
|
|
|
|
||||||
|
|
|
|
|
|
k |
2 |
|
|
|
|
|
|
где r0(t)- огибающая коэффициента корреляции rx(t)=Rx(t)/Dx
Учитывая,что r0(t)<<1 можно ограничиться двумя слагаемыми и использовать формулу
|
|
|
|
|
|
|
D x |
|
|
|
|
r 0 ( |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
B x( |
) |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
D x |
|
|
|
|
|
|
r 0 ( ) |
2 |
|
|
|
|
|
j |
|
|
|
|||
Тогда |
|
W y ( |
) |
|
|
|
|
|
|
R y ( |
) |
e |
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
e |
d |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|||||||||||||||||||||||||
Проблема:определить |
огибающю |
|
коэф.коррел. Предположим,что |
спектр.плотность |
|
мощ. |
||||||||||||||||||||||||||||||||||||||||||||||
вых.сигн имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
W y ( |
) |
|
|
W 0 |
e |
|
|
|
|
|
0 |
|
|
e |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
R x( |
|
) |
|
|
1 |
|
|
|
|
|
W x |
|
|
|
e j |
|
|
d |
cos |
|
|
|
a ( |
) |
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Применительно к рассматриваемому случаю можно записать |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
W 0 |
|
|
|
|
|
2 |
|
e j |
|
|
|
|
|
2 W 0 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
R x( |
) |
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
0 |
|
e |
|
|
cos |
|
( |
|
) d |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b 2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
cos |
( bx ) |
dx |
|
|
|
|
|
|
e |
|
|
|
||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Т.к. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
0 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
a ( ) |
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
R x( |
) |
|
|
|
|
|
|
|
e |
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
В итоге |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||
|
|
|
|
|
|
|
|
W |
|
|
|
|
|
|
|
|
R x( |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
r |
( ) |
|
|
|
|
|
e 4 |
|
|
cos |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|||||||||||||||||
R ( 0 ) |
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
r0 ( |
) |
|
|
|
e |
|
|
|
||||||||||
x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
D x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
!!! |
|
|
|
|
|
|
|
|
|
!!! |
|||||
Из этого следует:
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
D x |
|
r0 ( ) 2 |
|
|
D x |
|
D x |
|
|
|
|||
|
|
|
|
j |
j |
2 |
|
j |
|||||||
W y |
( ) |
|
|
1 |
|
e |
d |
|
e |
d |
|
e |
|
e |
d |
|
|
|
2 |
8 |
|||||||||||
|
2 |
|
4 |
|
|
|
|
|
|
|
|
||||
В результате получаем:
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
||||
|
|
|
|
D x |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
2 |
2 |
|
2 |
2 |
|||||||||||
W y ( ) |
D x |
( ) |
|
|
|
|
|
|
|
|
e |
D x |
( ) |
|
|
|
e |
||
|
|
|
|
2 |
|
|
|
|
|
||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
8 |
|
|
|
|||||
Спектральная плотность мощности сигнала на вых. амп. дет.