Шпора Автоген, СлучСигн, 2ой семестр (Надольский АН, Дубровский ВВ) [4242 вопросов] / doc / 38-43

38. Импульсная характеристика согласованного фильтра.

Рассмотрим импульсную характеристику h(t) согласованного фильтра. Учитывая, что g(t) любого фильтра связано c K(j) преобразованием Фурье, находим:

Импульсная характеристика:

.

Учитывая, что и вводя новою переменную , получим:

.

Т. е. если задан сигнал s(t), то импульсная характеристика определяется как:

.

Построение графика функции s(t₀––t): кривая s(-t) является зеркальным отражением заданного сигнала s(t). Функция же s(t₀—t) сдвинута относительно s(-t) на величину t₀ вправо, также зеркальна по отношению к исходному сигналу s(t), с осью симметрии проходящей через точку t₀/2.

Так как импульсная характеристика не может быть отрицательной, то t₀ не может быть меньше , чем Т_с (длительность сигнала).

При увеличении t₀ возрастание сигнала не будет, а будет наблюдаться сдвиг сигнала вправо. Условие t₀Т_с накладывает на сигнал требование его конечной длительности.

Вывод: Применение согласованной фильтрации возможно при импульсном сигнале или ограниченной по времени пачке импульсов.

39. Сигнал и помеха на выходе согласованного фильтра.

Используем соотношение: . Подставив в него получим:

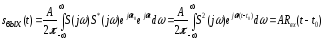
Т. е. выходной сигнал будет повторять форму корреляционную функцию смещенную во времени.

При t=t₀ R_вх=Э и выражение переходит в .

Рассмотри параметры шума. Наиболее распространен белый шум – нормальный шум со спектральной плотностью W₀=const. При действии нормального шума на линейную цепь на выходе шум остается нормальным и . Следовательно корреляционная функция шума на выходе:

Следовательно, корреляционная функция на выходе по форме совпадает с автокорреляционной функцией входного сигнала и с входным сигналом.

При =0 найдем дисперсию шума на выходе:

Найдем соотношение сигнал/шум на выходе согласованного фильтра (определим не по мощности а по напряжению: .

40. Синтез согласованного фильтра для прямоугольного видеоимпульса и прямоугольного радиоимпульса

Зададим сигнал как

Спектральная плотность такого сигнала: .

А его модуль: 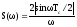.Используя оотношение найдем передаточную функцию согласованного фильтра: . Импульсная характеристика фильтра совпадает по форме с самим сигналом: .

Необходимо отметить, что сходящийся, т. е. фильтр физически реализуем.

Структурная схема имеет следующий вид. Множитель 1/j реализуется интегрирующим звеном, а множитель реализуется устройством вычитания сигнала без задержки и с задержкой Т_С. Реализация такого устройства в идеале невозможно, но можно получить хорошее приближение при использовании реальной интегрирующей RC-цепи, если обеспечить постоянную времени этой цепи, достаточно большую по сравнению с Т_с.

Получающийся при этом на выходе вычитающего устройства импульс может быть сделан достаточно близким к прямоугольному.

Спектр радиоимпульса представляется ф-лой:

В рассматр. случае

В результате прохождения фильтра получим:

42. Оптимальная фильтрация сигнала при «небелом» шуме.

Пусть на полностью известный сигнал накладывается небелый шум. Необходимо синтезировать фильтр с максимально возможным соотношением сигнал/шум на выходе.

Наиболее простой способ – это приведение заданного шума к белому. Рассмотрим следующую структурную схему. Здесь K(j) – искомая передаточная функция фильтра. А K₁(j) и 1/K₁(j) –вспомогательные четырехполюсники, введение которых не сказывается на работе устройства, так как их результирующая передаточная функция равна 1. Так как K₁(j) можно выбрать любую, то ее модуль зададим в виде , где W₀ – постоянная величина.

Тогда на выходе первого четырехполюсника будет действовать шум с равномерным энергетическим спектром , т. е. белый шум.

При этом меняется форма сигнала на выходе этого четырехполюсника, его спектральная плотность становится равной . Однако это не существенно , так как важно отношение энергии сигнала к энергетическому спектру шума, а форма сигнала при этом роли не играет.

Так как теперь шум белый, то последующая часть схемы должна иметь передаточную функцию отвечающую условию . Осуществив подстановку получим:

Подставив сюда выражение окончательно поучим: .

43.Проблемы цифровой обработки сигналов

Цифровая обработка сигналов обеспечивает:

-увеличение дальности связи

-высокую помехоустойчивость

-обработку, преобразование и хранение многомерных сигналов и изображений

-решение задач, невыполнимых на аналоговых уст-вах

Идр.

Спектр дискретного сигнала

1)Дискретный сигнал можно представить в виде:

S_д (t)=s(t)*y(t) (1) где s(t)-дискретизируемый сигнал y(t) –дискретизирующий

2)Сигнал y(t) считаем периодическим. Его спектр представим в видекомплексного ряда Фурье:

где dt

Подставив в формулу (1), получим:

Спектральная плотность дискретизируещего сигнала

Дискретизация прямоугольными импульсами

Подставив полученное выражение в S(jω)

Огибающая имеет форму

Центральная часть спектра дискретного сигнала повторяет по форме спектр непрерывного сигнала. Эта часть спектра не будет искажена, если частота дискретизации удовлетворяет условию ω₁ ≥2 ω_в –частота Найквиста

Аналогично производится дискретизация дельта-функции

Получается :

Спектральную плотность можно вычислить непосредственно по совокупности временных отсчетов