Шпора Автоген, СлучСигн, 2ой семестр (Надольский АН, Дубровский ВВ) [4242 вопросов] / doc / 36

36. Оптимальная фильтрация сигналов в условиях помех. Постановка задачи.

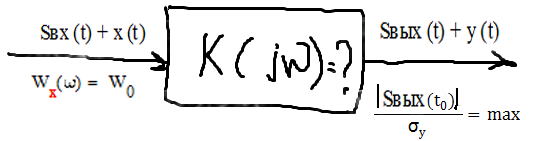
1. на вход поступает аддитивная смесь сигнала и шума Sвх(t) + x(t)

2. Шум белый W_x (w) = W₀

3. Задача решается в рамках линейной фильтрации Sвых(t) + y(t), т.е. Sвых(t) = f (Sвх(t))

y(t) = f ( x(t) )

4. Определить частотный коэффициент передачи лин. фильтра K ( jw ), который обеспечивает max отношение вых. сигнала в какой-то момент времени t₀ к среднеквадратическому значению шума на выходе

Для определения K ( jw) необходимо получить выражение и найти его максимум. Получим это выражение:

1. Получение

а) б)

в) берем обратное преобраз. Фурье :

2) Получение

а)

б)

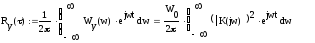
В)

Г) = Т.о. можно записать:

=

Для определения K ( jw), обеспечивающего максимум данного выражения, воспользуемся нер-вом Коши-Буняковского:

Левая часть будет max в случае равенства, а рав-во соблюдается при условии:

f₂(x) = A f₁* (x) , где А – произвольное число

f₁(x)  Sвх (jw) exp ( jwt₀ )

f₂ (x)  K ( jw )

Предположим, что условие f₂(x) = A f₁* (x) соблюдается, тогда можно записать:

=

=

= Э равенство Персиваля

= ,

запишем св-ва с учетом обозначений:

Перепишем получ. рав-во в след.виде :

Это равенство позволяет записать след:

1. K (w) = A Sвх (w) – АЧХ

2. фи (w) = - ( фи_s(w) + wt₀ )

Вывод : АЧХ фильтра с точностью до постоянного множителя равна амплитудному спектру вх. сигнала. Название такого фильтра – согласованный. Соглас. фильтр – фильтр, АЧХ которого согласована с амплитудным спектром вх. сигнала. ФЧХ фильтра равна фазовой хар-ке сигнала, взятого с обратным знаком.