
18. Стационарные и нестационарные случайные процессы. Их статические характеристики. Эргодические случайные процессы. З-ны распределения случ процессов позволяют определять практически все статичские характеристики. Однако при решении практических задач иногда нет возможности определить з-ны распределенияю такая невозможность возникает при решении некоторых задач линейных и нелинейных преобразований, механизм образования случ сигналов ли малоизучен. При решении когда числвые зхарактеристики можно определить без законов распределения. Числовые характеристики: мат ожидание, дисперсия, ковариационная ф-ция, корреляционная ф-ция. Важным классом случайных процессов является класс стационарных случайных процессов. Случайный процесс называется стационарным в узком смысле, если n-мерный закон распределения вероятности pn ( x1 , x2 ,..., xn ; t1 , t 2 ,..., t n ) зависит при любом n только от интервалов t 2 − t1 , t3 − t1 , ..., t n − t1 и не зависит от начала отсчета, то есть закон распределения инвариантен относительно одинакового сдвига точек t1 , t2 , ..., tn вдоль оси
времени. При этом p n ( x1 , x 2 ,..., x n ; t1 , t 2 ,..., t n ) = p n ( x1 , x 2 ,..., x n ; t 2 − t1 , t 3 − t1 ,..., t n − t1 ) .
Случ процесс называется стационарным в широком смысле, если данное определение относится только к n=1,2;
Широкость обусловлена тем, что при n=1,2 удовлетворяет больший класс сигналов. Устационарных в узком смысле случ процесса n-мерные плотности вер-сти ри всех n инвариантны. Это значит одномерная плотность вероятности не зависит от времени, двумерная плотность вероятность не зависит от времени а зависит от разности t 2 − t1.
Нестационарный случ процесс
Нестационарный случайный процесс




Стационарный случайный процесс



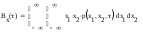
Для стационарных случ сигналов можно выделить след св-ва числовых характеристик 1)корреляц ф-ция случ процесса четная
2)дял
многих практических случаев выполн-ся
равенство

3)Дисперсия стац процесса равна значению корреляц ф-ции при τ=0
4)Абсолютное значение корреляц ф-ции не превышает её значение при τ=0
Случ процесс относится к классц эргодических, если его статистические характеристики можно определить не только путём усреднения по множеству реализаций но и усреденением по времени одной достаточно длинной реализации
Формулы числовых характеристик эргодического сигнала




