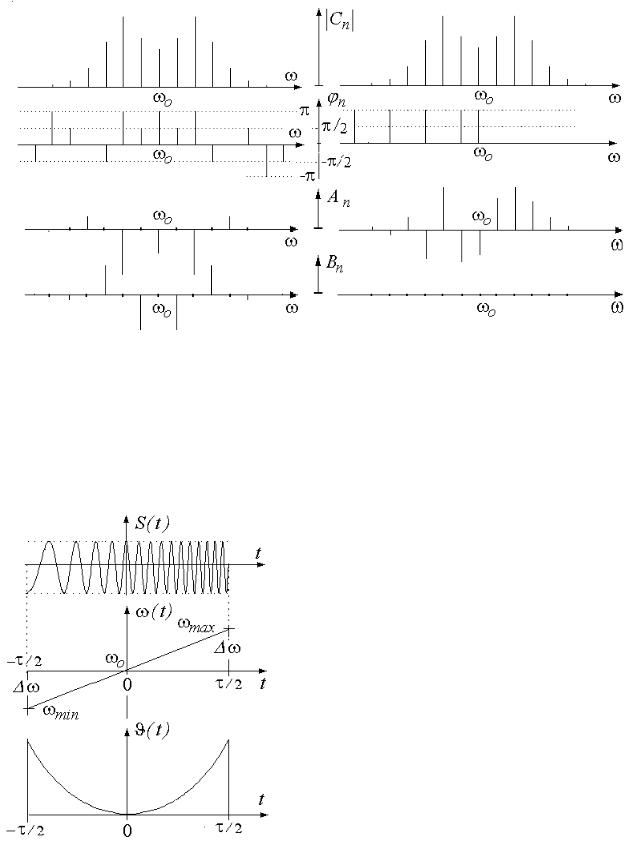
Рис.2.11. Спектры: ФМ – слева и ЧМ – справа при ϕо = 0, Φо = 0 и β = 3
2.3.3. Линейная частотная модуляция (ЛЧМ)
На практике используются радиоимпульсы (рис.2.12), частота которых ме- няется по линейному закону:
|
|
|
|
ω( t ) = ωo + αt, |
|
|
|
|
(2.47) |
||||||
|
|
где |
α = 2 |
ω / τ , |
ω = 2π |
f |
– |
девиация |
|||||||
|
|
частоты, τ - длительность импульса. |
|||||||||||||
|
|
Частота |
изменяется |
в |
пределах |
от |
|||||||||
|
|
ωmin = ωo − |
ω |
до |
ωmax = ωo + |
ω. |
|||||||||
|
|
Фаза сигнала модуляции |
|
|
|
|
|
|
|||||||
|
|
ϑ( t ) = ò |
αt dt = |
1 |
αt2 , |
|
t |
|
≤ |
τ |
. (2.48) |
||||
|
|
|
|
||||||||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Период |
колебания |
средней |
частоты |
||||||||||
|
|
To = 2π / ωo = 1/ fo . Число периодов То на |
|||||||||||||
|
|
длине τ равно No = τ / To . Глубина моду- |
|||||||||||||
|
|
ляции частоты m = |
ω / ωo = |
|
f / fo . |
|
|||||||||
|
|
Основным |
|
параметром |
|
ЛЧМ-сигнала |
|||||||||
|
|
является его база В, равная произведению |
|||||||||||||
Рис.2.12. ЛЧМ-сигнал |
длительности τ на девиацию |
f |
3: |
|
|||||||||||
|
|
f τ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 Ряд авторов называют базой сигнала величину2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
29 |
PDF created with pdfFactory Pro trial version www.pdffactory.com
B = f τ = Nom. |
(2.49) |
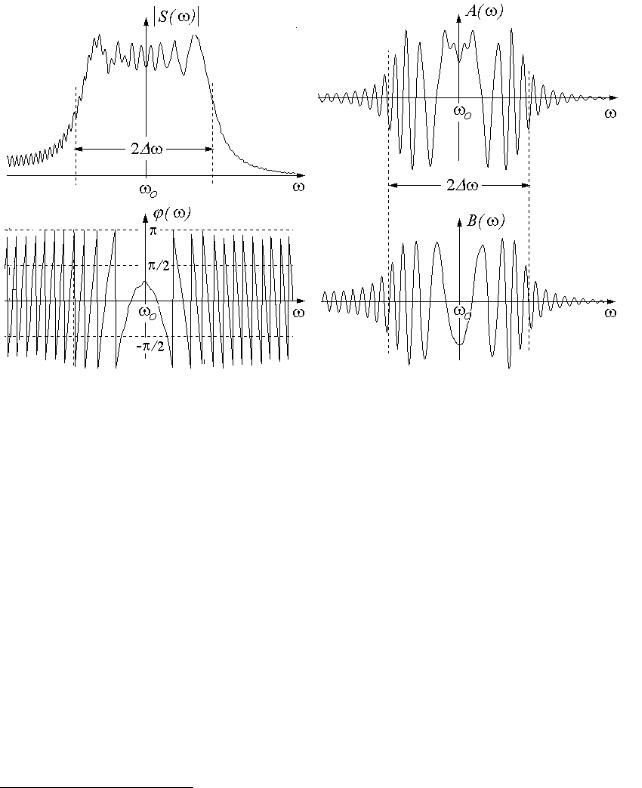
Спектр колебания (рис.13) достаточно сложен. Он выражается через специ- альные функции – интегралы Френеля. Благодаря тому, что согласно (2.48) фаза ϑ(t) здесь функция четная, все составляющие спектра имеют четное рас- пределение относительно частоты wo (табл.1, вариант 1.2).
Рис.2.13. Спектр ЛЧМ-сигнала с базой В = 15 и ϕo = 0
Модуль ½S(ω)½ по форме похож на трапецию, ширина которой по половинной высоте равна 2Δω, а склоны тем круче, чем больше база В. Фазовый спектр
описывается формулой
j(w) » |
p |
|
B æ w - w |
ö2. |
|||
|
- |
|
ç |
o ÷ . |
|||
4 |
2 |
||||||
|
|
è |
w |
ø |
|||
ЛЧМ-сигналы широко используются в системах оптимального приема дальней радиолокации, и в этой связи важную роль играет их автокорреляци- онная функция, огибающая которой по форме близка к функции Sin ωt / ωt
(рис.2.14) 4, с шириной лепестков
t ≈ |
|
1 |
= |
τ |
. |
(2.50) |
2 |
f |
|
||||
|
|
2B |
|
|||
В пределах центрального лепестка шириной 2Dt укладывается N периодов То колебаний несущей частоты:
4 Это утверждение, учитывая форму спектра, предлагается обосновать самостоятельно.
30
PDF created with pdfFactory Pro trial version www.pdffactory.com