Раздел 2. Спектральный анализ сигналов. Радиосигналы
2.1. Общие сведения о модулированных колебаниях и их спектрах
Радиосигналами (РС) называют электромагнитные колебания высокой частоты (обычно выше 100 кГц), предназначенные для передачи через эфир сообщений, вводимых в РС путем модуляции (изменения) их параметров. Раз- личают амплитудную (АМ), угловую (УМ), амплитудно-угловую (АУМ), ам- плитудно-импульсную (АИМ), фазово-импульсную (ФИМ), широтно- импульсную (ШИМ) и другие виды модуляции.
При АМ, УМ и АУМ в качестве несущего используется гармоническое ко- лебание. Эти виды сигналов описываются формулой
|
S( t ) = U( t ) CosΨ ( t ) , |
(2.1) |
|
где |
Ψ(t) = ωot + ϕ(t) , |
ϕ(t) = ϑ(t) + ϕo , |
(2.2) |
ωо – частота несущего колебания, ϕо – его начальная фаза, U(t) и ϑ(t) – амплиту-
да и фаза, изменяемые в соответствии |
с управляющим сигналом модуляции |
||||||
UM (t) . Для колебаний с УМ и |
АУМ вводится понятие мгновенной или теку- |
||||||
щей частоты ω(t), связанной с фазой сигнала ψ(t) соотношениями |
|
||||||
ω(t) = |
dΨ(t) |
= ωo + |
dϕ(t) |
= ωo + |
ω(t), |
Ψ(t) = òω(t) dt . |
(2.3) |
dt |
dt |
||||||
Модуляция, при которой частота не меняется, а амплитуда U(t) ~UM (t), |
|||||||
называется амплитудной. |
Модуляция называется угловой, если модулируется |
||||||
фаза Ψ(t), а амплитуда U(t)=Uo остается постоянной. При амплитудно-угловой модуляции изменяются и U(t), и Ψ(t), каждая по своему закону. В импульсных видах модуляции в качестве несущего используются колебания, по форме от- личные от гармонического (обычно прямоугольные).
Важную роль в процессе обработки РС при их передаче и приеме играет
знание спектральных характеристик РС. |
|
Действительный сигнал S(t), описываемый формулой (2.1), может рас- |
|
сматриваться как реальная часть комплексного сигнала Z(t): |
|
S( t ) = Re( Z( t )) = 1 ( Z( t ) + Z*( t )), где Z( t ) = U( t )eΨ ( t ) . |
(2.4) |
2 |
|
16
PDF created with pdfFactory Pro trial version www.pdffactory.com
Введем в рассмотрение функцию модуляции CM(t) и комплексную амплитуду
сигнала C(t) со спектрами CM ( ω) и C( ω), определив их как
ì |
|
|
|
|
|
|
jϑ( t ) |
Û CM (ω ) = |
|
CM (ω ) |
|
|
|
jϕM (ω ) |
, |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ïCM ( t ) = U( t )e |
|
|
|
|
|
|
e |
|
|
||||||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
C(ω ) |
|
e jϕc(ω ) , |
. |
(2.5) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
í C( t ) =U( t )e j( ϑ( t )+ϕo ) Û C(ω ) = |
|
||||||||||||||||||
ï |
|
CM (ω ) |
|
= |
|
C(ω ) |
|
, |
ϕc(ω ) =ϕM (ω ) + ϕo . |
|
|
||||||||
|
|
|
|
|
|
||||||||||||||
ï |
|
|
|
|
|
|
|||||||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
Z(t) = U (t) eΨ(t) = CM (t) e j(ωot+ϕo ) = C(t) e jωot . |
(2.6) |
||||
Спектр функции C(t) на основании преобразования Фурье равен |
|
|||||
|
C( w) = ò∞ C( t )e− jωtdt = |
|
C( w) |
|
e j ϕc( ω) = Ac( w) - jBc( w) , |
(2.7) |
|
|
|
||||
|
−∞ |
|
|
|
|
|
где ½С(ω ½ и ϕc( ω) - его модуль и фаза, а Ac( ω) и Bс(ω) – действительная и мнимая части, равные
ì |
|
|
|
|
C(ω) |
|
Cosϕ |
|
|
(ω) = |
|
|
∞ |
U (t) Cos(ωt - j(t)) dt , |
|
||||||||||||
ïA (ω) = |
|
|
|
|
|
|
|||||||||||||||||||||
ï |
|
c |
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
ò−∞ |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
(2.8) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
íBc (ω) = - |
|
|
C(ω) |
|
Sinϕc (ω) = ò−∞U (t) Sin(ωt - j(t)) dt , |
||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- Bc (ω ) |
|
|
ï |
|
C(ω) |
|
= |
A (ω )2 + B |
c |
(ω)2 |
, |
ϕ |
c |
(ω )= arc tg |
. |
|
||||||||||||||
|
|
|
|||||||||||||||||||||||||
ï |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
Ac (ω) |
|
|||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Спектр функции Z( t ) = C( t )e jωot |
|
|
согласно спектральной теореме смещения |
||||||||||||||||||||||||
будет равен спектру C(ω ), перенесенному на частоту wо : |
|
||||||||||||||||||||||||||
|
|
|
|
Z( w) = C( w - wo ) = |
|
C( w - wo ) |
|
e j ϕc( ω−ωo ). |
(2.9) |
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
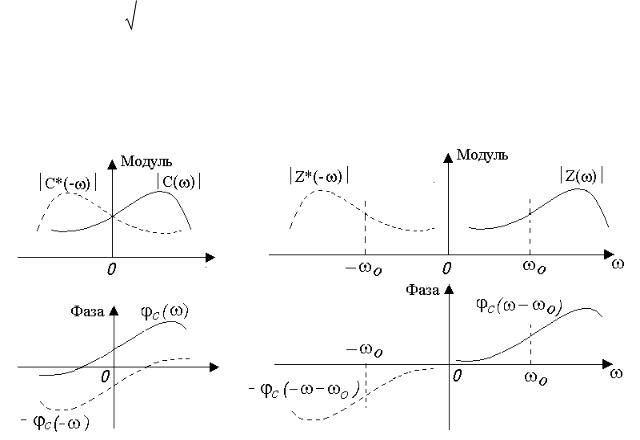
Рис.2.1. Спектры функций C(t), C*(t), Z(t) и Z*(t). Сплошные линии - C(ω), Z(ω), пунктир - C*(-ω), Z*(-ω)
17
PDF created with pdfFactory Pro trial version www.pdffactory.com
Заметим, что в силу комплексности C(t) и Z(t) их спектры (рис.1) не об-
ладают симметрией относительно частот w = 0 и w = wо . |
|
||||||||||||||||||||||||
Спектры комплексно-сопряженных функций C*(t) |
и Z*(t) будут |
|
|||||||||||||||||||||||
ì |
|
|
|
= |
|
C( -w) |
|
e |
− j ϕc( −ω) |
= Ac( -w) + jBc( |
-w), |
|
|||||||||||||
|
|
|
|||||||||||||||||||||||
ïC * ( -w) |
|
|
|
|
|
|
|
|
|
(2.10) |
|||||||||||||||
í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e − jϕc ( −ω−ωo ). |
||
ïZ * ( -w) |
= C * ( -w - w )= |
|
C( -w - w ) |
|
|
||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
o |
|
|
|
|
|
o |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
На рис.1 они изображены пунктиром. |
|
|
|
|
|
||||||||||||||||||||
Возможны различные формы спектра сигнала S(t). Одна из них вытекает |
|||||||||||||||||||||||||
из формулы S( t ) = Re Z( t ), согласно которой |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
S(t) = Re( |
1 |
ò∞ Z(ω)e jωt dω) = |
|
|
|||||||||||||
|
|
|
|
|
|
|
2π |
|
|
||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
||||||
= Re[ |
ò∞ (Ac (ω - ωo ) - jBc (ω - ωo )) (Cosωt + jSinωt) dω] = |
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
2π |
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.11) |
||||||
|
|
1 |
|
ò∞ (Ac (ω - ωo ) Cosωt + Bc (ω - ωo ) Sinωt) dω = |
|||||||||||||||||||||
= |
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
2π −∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
= |
1 |
∞ |
|
C(ω - ωo ) |
|
Cos(ωt + jc (ω - ωo )) dω . |
|
||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
2π |
ò−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Подынтегральные функции – это составляющие спектра. Они действительные,
и отсюда |
|
форма представления спектра его компонентами Ac( ω − ωo ), |
||
Bc( ω − ωo ), |
|
C( ω − ωo ) |
|
и ϕc( ω − ωo ) называется действительной. Эти ком- |
|
|
|||
поненты совпадают с компонентами спектра комплексной амплитуды C( ω), сдвинутыми на частоту ωo . В общем случае они не обладают какой-либо сим- метрией ни относительно частоты ω = 0, ни относительно частот ± ωo и по этой причине требуют задания на всей оси частот от − ∞ до ∞ (рис.2.2).
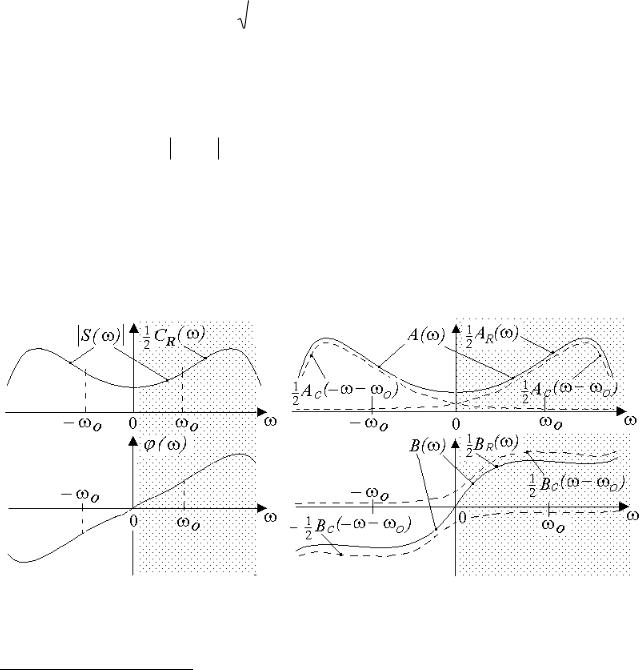
а |
б |
Рис.2.2. |
Компоненты действительной формы спектра: |
а – модуль и фаза; б – косинусная и синусная составляющие
18
PDF created with pdfFactory Pro trial version www.pdffactory.com
Другая форма спектра S( ω) , иногда называемая комплексной 1, основана на представлениях (2.4), (2.9) и (2.10), согласно которым
|
|
|
|
|
|
|
|
S(ω ) = |
|
1 |
( Z(ω ) + Z * ( -ω )) = |
|
|
|
|
|
|
|||||||||||||||
|
1 |
2 |
|
|
(2.12) |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
[C(ω - ωo )+ C * ( -ω - ωo ) ]= A(ω ) - jB(ω ) = |
|||||||||||||||||||||||||||||||
= |
|
S(ω ) |
|
e jϕ(ω ) , |
||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
2 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
ìA(ω) = A(-ω) = |
|
|
(A (ω - ω |
o |
) + A (-ω - ω |
o |
)) , |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
ï |
|
|
|
|
|
|
2 |
|
|
|
c |
|
|
|
c |
|
|
|
|
|
|
|
|||||||||
|
ï |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
ïB(ω) = -B(-ω ) = |
(B |
c |
(ω - ω |
o |
) - B |
c |
(-ω - ω |
o |
)) , |
|
|
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
где |
ï |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
(2.13) |
||||||||||||||
í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
ï |
|
S(ω) |
|
= |
|
S(-ω) |
|
= |
A2 (ω) + B 2 (ω) , |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- B(ω ) |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
ï |
|
|
|
|
|
|
= arctg |
. |
|
|
|
|
|
|
|
|
|||||||||||||||
|
ï j(ω) = -j(-ω ) |
A(ω) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Характерным для спектра (см. рис.2.2) является эрмитовая симметрия S(ω ) = = S*(-ω ) относительно частоты ω = 0 и отсутствие симметрии относительно частот ±ωо . Модуль S( ω) и действительная часть A( ω) - четные, фаза ϕ( ω)
и мнимая часть B( ω) - нечетные. Функции A( ω) и B( ω) складываются из со- ставляющих Ac ( ±ω − ωo ) , Bc ( ±ω − ωo ) (назовем их сопряженными), отно- сящихся к частотам ± ωo . Если спектры этих составляющих достаточно протя-
женны, то они, перекрываясь, накладываются "хвостами" и создают спектры A( ω) и B( ω), которые могут весьма заметно отличаться от их сопряженных слагаемых (рис.2.3).
а б Рис.2.3. Комплексный и действительный спектры модулированного ра-
диосигнала: а – модуль и фаза, б - четная и нечетная составляющие
1 Такая форма используется в программе SAS.
19
PDF created with pdfFactory Pro trial version www.pdffactory.com
Если перекрытия нет, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ìпри ω > 0 |
имеем |
A(ω) = |
1 |
|
A (ω - ω |
|
) , B(ω) = |
1 |
B |
(ω - ω |
|
) , |
|
|
|||
|
|
o |
|
o |
|
|
|||||||||||
ï |
|
2 |
|
c |
|
2 |
c |
|
|
|
|
|
(2.14) |
||||
í |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|||
ïпри ω < 0 |
имеем |
A(ω) = |
|
A (-ω - ω ) , B(ω) = - |
B (-ω - ω |
|
). |
||||||||||
|
|
|
|||||||||||||||
î |
|
2 |
|
c |
|
o |
|
|
2 |
c |
|
|
o |
|
|||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Еще одна действительная форма спектра S( ω) |
есть разновидность ком- |
||||||||||||||||
плексной формы. Она является следствием эрмитовой сопряженности |
S( ω) , |
||||||||||||||||
благодаря которой для расчета сигнала S(t) достаточно вести интегрирование только в области положительных частот:
|
|
|
1 |
∞ |
|
|
1 |
|
∞ |
|
||||||
|
|
S( t ) = |
òS( w)e jωtdw = |
|
|
ò( S( w) + S * ( w))e jωtdw = |
|
|||||||||
|
|
2p |
2p |
|
||||||||||||
|
|
|
−∞ |
|
0 |
(2.15) |
||||||||||
|
1 |
∞ |
|
|
|
|
|
|
|
|
1 |
|
∞ |
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
= |
|
òCR( w)Cos( wt + ϕ( w))dw = |
|
|
|
|
ò( AR( w)Coswt + BR( w)Sinwt )dw. |
|||||||||
2p |
|
2p |
||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Здесь |
CR( ω) = 2 |
|
S( ω) |
|
, |
AR( ω) = 2A( ω) , BR( ω) = 2B( ω) . |
(2.16) |
|||||||||
|
|
|||||||||||||||
Эта форма удобна тем, что для изображения составляющих спектра достаточна область только положительных частот рис.2.3. Если сопряженные спектры не перекрываются, то составляющие CR , AR , BR - те же, что у комплексной ам-
плитуды C(t), но перенесенные на частоту ωo :
ìA ( w) = A ( w - w ), |
B |
R |
( w) = B ( w - w ), |
|
||||
í R |
c |
o |
|
c |
o |
|
||
îCR( w) = |
C( w - wo ) |
, |
ϕ( w) = ϕc( w - wo ). |
(2.17) |
||||
Если функция модуляции C(t) периодическая с периодом Т, то спектр сиг- нала S(t) будет дискретным с шагом Ω =2π / T и составляющими, расположен- ными на частотах ωk = ωo + Ω k , амплитуды которых равны S( ωk ) / T .
Одной из важных характеристик радиосигнала является наличие или от- сутствие симметрии его спектра относительно несущей частоты ωo , о чем
можно судить по симметрии спектра его комплексной амплитуды С(ω), кото- рая, в свою очередь, определяется симметрией функций его амплитуды U(t) и фазы j(t). Результаты соответствующего анализа сведены в табл.2.1.
20
PDF created with pdfFactory Pro trial version www.pdffactory.com