
Краткие шпоры по радиотехническим системам РТС [3030 вопросов]
.docЗадача 3.1.М-последовательность описывается полиномом Х4+Х3+1. Нарисуйте структурную схему генератора; сформируйте одиночную последовательность и вычислите автокорреляционную функцию. Какой максимальный уровень бокового остатка автокорреляционной функции.

 δбок=
3
δбок=
3
Задача 3.2.Сложный сигнал с линейной частотной модуляцией длительности 10 мкс и средней частотой спектра f0=1010 Гц имеет время корреляции τк=0.5 мкс. Определите эффективную полосу сигнала, его базу и оцените разрешение по дальности и радиальной скорости, которые обеспечивает данный сигнал.
Определим разрешение по дальности:
![]()
Определим разрешение по скорости:
![]()
Определим эффективную полосу сигнала:
![]()
Определим базу сигнала:
![]()
Задача 3.3. Согласованный фильтр настроен на прием цифрового сигнала 111-11 на фоне белого шума. Какова импульсная характеристика? Построить временные диаграммы полезного выходного сигнала и автокорреляционную функцию шума на выходе фильтра. Какое отношение сигнал/шум на выходе фильтра, если входное отношение сигнал/шум равно 0 дБ? Считать коэффициент ослабления согласованным фильтром равным 1.
![]() g(t)=1-1111
g(t)=1-1111


![]()
![]()
Задача 3.4. Радиоимпульс с флюктуирующей по закону Релея амплитудой и равновероятной начальной фазой принимается оптимальным обнаружителем на фоне гауссовского белого шума. Средняя энергия радиоимпульса составляет 3.6 мкДж; а белый шум на сопротивлении в 1 Ом выделяет мощность 4 Вт в полосе 10 МГц. Определить вероятность правильного обнаружения, если вероятность ложной тревоги равна 0.1. Какое пороговое напряжение необходимо установить в обнаружителе?
Определим спектральную плотность шума:
![]()
Определим отношение сигнал/шум на входе:
![]()
Определим вероятность правильного обнаружения:

Определим пороговое напряжение:

Задача 3.5. При оптимальном различении на фоне гауссовского шума четырех равновероятностных известных симплексных сигналов обеспечивается входное отношение сигнал/шум (по мощности) равное 12. Какова вероятность ошибки различителя? Как изменится вероятность ошибки оптимального различителя, если начальные фазы различаемых сигналов неизвестны и равновероятны. Нарисуйте структурные схемы оптимальных различителей для указанных условий.
Для данного случая определим коэффициент взаимной корреляции:
![]()
Определим эквивалентное отношение сигнал/шум:
![]()
Определим вероятность ошибки когерентного различителя:
![]()
Определим вероятность ошибки некогерентного различителя:
![]()
![]()
Вывод: вероятность ошибки возрастет в 8 раз

Когерентный различитель Некогерентный различитель
Задача 3.6. В импульсной РЛС в качестве зондирующего сигнала используется радиоимпульс с f0=1010 Гц и прямоугольной огибающей длительностью 1 мкс. Какова потенциальная точность совместных измерений дальности и радиальной скорости РЛС, если минимальное отношение сигнал/шум по мощности на входе приемника равно 10? Прием отраженного сигнала осуществляется на фоне гауссовского белого шума.
Оценим потенциальную точность измерения временных параметров сигнала:

Оценим потенциальную точность измерения частотных параметров сигнала:
![]()
Определим потенциальную точность измерения дальности:
![]()
Определим потенциальную точность измерения радиальной скорости:
![]()
Задача 3.7. Импульсной когерентная РЛС с вероятностью обнаружения 0.9 и вероятностью ложной тревоги 0.01 обеспечивает обнаружение отраженного сигнала с потенциальными точностями измерения дальности 200 м и радиальной скорости 4 м/с. Какими параметрами должен обладать зондирующий сигнал со средней частотой спектра f0=1010 Гц.
Определим отношение сигнал/шум:

Оценим потенциальную точность измерения временных параметров сигнала:
![]()
Оценим потенциальную точность измерения частотных параметров сигнала:

Определим эффективную полосу сигнала:

Определим эффективную длительность сигнала:

Определим базу сигнала:
![]()
Задача 3.8. Импульсной когерентная РЛС обеспечивает Разрешающую способность по дальности и радиальной скорости соответственно 100 м и 2 м/с. Какими параметрами должен обладать зондирующий сигнал со средней частотой спектра f0=1010 Гц.
Определим время корреляции сигнала:
![]()
Определим длительность сигнала:

Определим базу сигнала:
![]()
Задача 3.9. Сообщение состоит из 600 символов алфавита
а1(р1=0.5), а2(р2=0.25), а3(р3=0.125), а4(р4=0.0625), а5(р5=0.0625)
Сколько потребуется двоичных разрядов для передачи сообщения при оптимальном (статистическом) зондировании и равномерном безизбыточном кодировании.
Определим число разрядов для передачи одного символа:
![]()
Определим число разрядов для передачи сообщения при равномерном безизбыточном кодировании:
![]()
Определим число разрядов для передачи сообщения при оптимальном (статистическом) зондировании:
![]()
![]()
![]()
Задача 3.10. Пропускная способность канала связи с аддитивным белым гаусовским шумом составляет 1000 бит/с при отношении сигнал/шум по мощности 0,1. Как изменится пропускная способность канала, если полосу канала увеличить в 2 раза.
Воспользуемся формулой Шеннона:
![]()
Выражение для отношения сигнал/шум имеет вид:
![]()
Так как шум гауссовский, то:
![]()
Определим пропускную способность в исходном состоянии:
![]()
Определим пропускную способность при расширении полосы в два раза состоянии:
![]()
Возьмем отношение:
![]()
Задача 3.11. Цифровая информация передается двумя противоположными сигналами S1(t) и S2(t). Какова вероятность ошибки приема сигналов когерентным оптимальным приемником на фоне гауссовского белого шума, если отношение сигнал/шум (по мощности) на входе приемника равно 8, сигналы равновероятны, канал связи симметричный без памяти?
Нарисуйте структурную схему приемника системы.
Приемник можно построить на согласованном фильтре:

Приемник можно построить на корреляторе:

Формула для нахождения вероятности ошибки имеет вид:
![]()
Задача 3.12. Цифровая информация передается двумя ортогональными сигналами S1(t) и S2(t) с одинаковыми энергиями. Какова вероятность ошибки приема сигналов некогерентным приемником на фоне гауссовского белого шума, если отношение сигнал/шум (по мощности) на входе приемника равно 10, а канал связи симметричный без памяти? Нарисуйте структурную схему приемника системы.
Приемник можно построить на согласованном фильтре:

Формула для нахождения вероятности ошибки имеет вид:
![]()
Задача 3.13. Дискретная информация передается четырьмя равновероятными сигналами S1(t), S2(t) , S3(t) , S4(t) равных энергий. Какова вероятность ошибочного приема дискретной информации некогерентным приемником на фоне гауссовского белого шума, если отношение сигнал/шум (по мощности) на входе приемника равно 10? Канал связи симметричный без памяти. Нарисуйте структурную схему приемника системы.
Приемник можно построить на согласованном фильтре:

Формула для нахождения вероятности ошибки имеет вид:
![]()
Задача 3.14. Цифровая информация передается двумя равновероятными инверсными псевдослучайными ФМ сигналами S1(t) и S2(t). Какова вероятность ошибочного приема информации когерентным оптимальным приемником на фоне гауссовского белого шума, если отношение сигнал/шум (по мощности) на входе приемника равно 1, база сигналов В=16, канал связи симметричный без памяти? Нарисуйте структурную схему приемника системы.
Приемник можно построить на согласованном фильтре:

Приемник можно построить на корреляторе:
 Определим отношение
сигнал/шум на выходе приемника:
Определим отношение
сигнал/шум на выходе приемника:
![]()
Формула для нахождения вероятности ошибки имеет вид:
![]()
Задача 3.15. Приведите схему беспоискового приемника ФМ ПС - сигналов с информационной манипуляцией по задержке. Какое отношение сигнал/шум (по мощности) необходимо иметь на входе приемника, чтобы обеспечить вероятность ошибки 10-3, если базы сигналов В=64, прием на фоне белого шума.
Схема беспоискового приемника имеет вид:

Формула для нахождения вероятности ошибки имеет вид:
![]()
Из этой формулы можно найти отношение сигнал/шум на выходе приемника:
![]()
Формула для нахождения отношение сигнал/шум на выходе приемника имеет вид:
![]()
Подставив численные значения переменных, получим:
![]() или в виде уравнения
или в виде уравнения
![]()
Решив уравнение,
получим:
![]() и
и
![]()
Так как
![]() ,
то окончательный ответ
,
то окончательный ответ
![]() .
.
Задача 3.16.
Приведите схему квазикогерентного
приемника АМ-сигнала ![]() ,
если помеха – белый гауссовский шум.
,
если помеха – белый гауссовский шум.

Задача 3.17.
Приведите схему квазикогерентного
приемника АМ-сигнала с подавленной
несущей![]() ,
если помеха – белый гауссовский шум.
,
если помеха – белый гауссовский шум.

Задача 3.18.
Приведите схему квазикогерентного
приемника ФМ-сигнала
![]() ,
где
,
где
![]() - сообщение,
- сообщение,
![]() ,
,![]() ,
,![]() - известные величины. Помеха – белый
гауссовский шум.
- известные величины. Помеха – белый
гауссовский шум.

Задача 3.19.
Приведите схему квазикогерентного
приемника шумоподобного ФМ-сигнала
![]() ,
где
,
где
![]() - псевдослучайная последовательность,
- псевдослучайная последовательность,
![]() и
и
![]() - флуктуирующие
задержка и фаза. Помеха – белый гауссовский
шум.
- флуктуирующие
задержка и фаза. Помеха – белый гауссовский
шум.

Задача 3.20.
Приведите схему некогерентного приемника
ЧМ-сигнала
![]() ,
где
,
где
![]() - случайная начальная фаза,
- случайная начальная фаза,
![]() -
сообщение. Помеха – белый гауссовский
шум.
-
сообщение. Помеха – белый гауссовский
шум.

или

Задача 3.21.
Приведите схему некогерентного приемника
шумоподобного ФМ-сигнала
![]() ,
где
,
где
![]() - случайная начальная фаза,
- случайная начальная фаза,
![]() - задержка. Помеха
– белый гауссовский шум.
- задержка. Помеха
– белый гауссовский шум.

Задача 3.22.
Приведите схему и характеристику
безынерционного нелинейного преобразователя
для помехи с ПРВ
 .
.

![]()
![]()


Задача 3.23.
Приведите схему и характеристику
безынерционного нелинейного преобразователя
для помехи с ПРВ
 .
.


![]()


Задача 3.24.
Приведите схему и характеристику
безынерционного нелинейного преобразователя
для помехи с ПРВ
![]() .
.


![]()
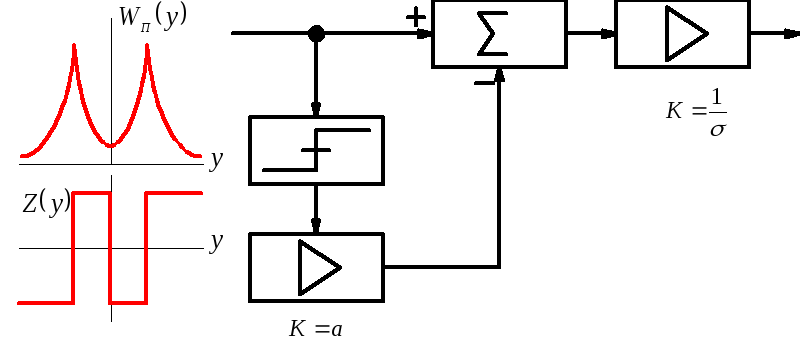
Задача 3.25.
Приведите схему адаптивного безынерционного
нелинейного преобразователя для помехи
с ПРВ
 .
Мода а оценивается
на интервале [0,T].
Отсчеты помехи считать независимыми.
.
Мода а оценивается
на интервале [0,T].
Отсчеты помехи считать независимыми.



![]()

Задача 3.26.
Приведите схему приемника ФМ-сигнала
![]() ,
если помеха с независимыми отсчетами
имеет ПРВ
,
если помеха с независимыми отсчетами
имеет ПРВ
 .
.

![]()
![]()

Задача 3.27.
Приведите
схему приемника ЧМ-сигнала со случайной
начальной фазой
![]() ,
если помеха с независимыми отсчетами
имеет ПРВ
,
если помеха с независимыми отсчетами
имеет ПРВ
 .
.

![]()
![]()

Задача 3.28.
Приведите схему приемника шумоподобного
ФМ-сигнала
![]() ,
где
,
где
![]() - ПСП,
- ПСП,
![]() случайно изменяющаяся задержка, помеха
– шум с ПРВ
случайно изменяющаяся задержка, помеха
– шум с ПРВ
 .
.


![]()

Задача 3.29.
Приведите схему приемника ФМ-сигнала
![]() ,
если помеха с независимыми отсчетами
имеет ПРВ
,
если помеха с независимыми отсчетами
имеет ПРВ
 .
.

![]()

Задача 3.30.
Приведите схему квазикогерентного
приемника для шумоподобного ФМ-сигнала
![]() ,
если помеха имеет ПРВ
,
если помеха имеет ПРВ
 ,
,
![]() ,
,
![]() - случайно изменяющиеся задержка и фаза
сигнала.
- случайно изменяющиеся задержка и фаза
сигнала.
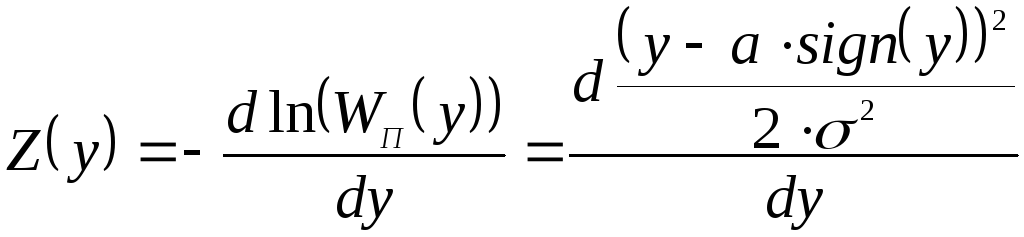

![]()

